We study the existence of equilateral triangles of given side
lengths and with integer coordinates in dimension three. We show
that such a triangle exists if and only if their side lengths are of
the form
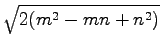
for some integers
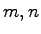
. We also
show a similar characterization for the sides of a regular
tetrahedron in
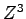
: such a tetrahedron exists if and only
if the sides are of the form
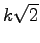
, for some
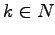
.
The classification of all the equilateral triangles in
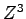
contained in a given plane is studied and the beginning analysis for
small side lengths is included. A more general parametrization is
proven under special assumptions. Some related questions about the
exceptional situation are formulated in the end.


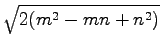 for some integers
for some integers