 |
Journal of Integer Sequences, Vol. 10 (2007), Article 07.1.6 |
 |
Journal of Integer Sequences, Vol. 10 (2007), Article 07.1.6 |
Florian Luca
Mathematical Institute, UNAM
Ap. Postal 61-3 (Xangari)
CP 58 089
Morelia, Michoacán
Mexico
Abstract:
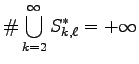 .
.
Received January 5 2006; revised version received December 30 2006. Published in Journal of Integer Sequences December 30 2006.