 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.6.6 |
 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.6.6 |
V. Janitzio Mejía Huguet
Departamento de Ciencias Básicas
Universidad Autónoma Metropolitana-Azcapotzalco
Av. San Pablo #180
Col. Reynosa Tamaulipas
C. P. 02200, Azcapotzalco DF
México
Florin Nicolae
Institut für Mathematik
Technische Universität Berlin
MA 8-1, Strasse des 17 Juni 136
D-10623 Berlin
Germany
and
Institute of Mathematics
Romanian Academy
P.O. Box 1-764, RO-014700, Bucharest
Romania
Abstract:
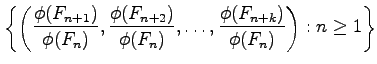
(Concerned with sequence A000045.)
Received May 20 2009; revised version received September 22 2009. Published in Journal of Integer Sequences, September 22 2009.