 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.1.2 |
 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.1.2 |
Timo Tossavainen
School of Applied Educational Science and Teacher Education
University of Eastern Finland
P.O.Box 86, FI-57101 Savonlinna
Finland
Abstract:
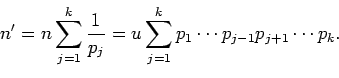
(Concerned with sequences
A000040
A003415
A005117.)
Received October 30 2012; revised version received January 1 2013. Published in Journal of Integer Sequences, January 1 2013.