We consider a
generalized Fibonacci sequence (
Gn ) by
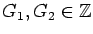
and
Gn =
Gn-1 +
Gn-2 for any integer
n.
Let
p be a prime number and let
d(
p) be the smallest positive integer
n which satisfies
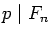
.
In this article, we introduce equivalence relations for the set of generalized Fibonacci sequences.
One of the equivalence relations is defined as follows.
We write
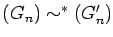
if there exist integers
m and
n satisfying
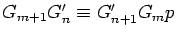
.
We prove the following: if
p ≡ 2 (mod 5),
then the number of equivalence classes
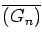
satisfying
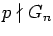
for any integer
n is
(
p+1)/
d(
p)-1.
If
p ≡ ± 1 (mod 5), then
the number is
(
p-1)/
d(
p)+1.
Our results are refinements of a theorem given by Kôzaki and Nakahara in 1999.
They proved that there exists a generalized Fibonacci sequence (
Gn )such that
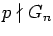
for any
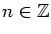
if and only if one of the following three conditions holds:
(1)
p = 5; (2)
p ≡ ± 1 (mod 5);
(3)
p ≡ 2 (mod 5)
and
d(
p)<
p+1.
Received November 7 2015; revised versions received January 18 2016; January 20 2016; January 25 2016.
Published in Journal of Integer Sequences, February 5 2016.

