Journal of Integer Sequences, Vol. 4 (2001), Article 01.2.1

Arithmetic and growth of periodic orbits


Yash Puri1 and Thomas Ward
School of Mathematics
University of East Anglia
Norwich NR4 7TJ, U.K.

Email: t.ward@uea.ac.uk

Abstract: Two natural properties of integer sequences are introduced and studied. The first, exact realizability, is the property that the sequence coincides with the number of periodic points under some map. This is shown to impose a strong inner structure on the sequence. The second, realizability in rate, is the property that the sequence asympototically approximates the number of periodic points under some map. In both cases we discuss when a sequence can have that property. For exact realizability, this amounts to examining the range and domain among integer sequences of the paired transformations

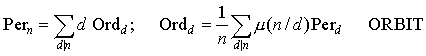
that move between an arbitrary sequence of non-negative integers Orb counting the orbits of a map and the sequence Per of periodic points for that map. Several examples from the Encyclopedia of Integer Sequences arise in this work, and a table of sequences from the Encyclopedia known or conjectured to be exactly realizable is given.

1The first author gratefully acknowledges the support of E.P.S.R.C. grant 96001638

Full version:  pdf,    dvi,    ps,    tex   

(Concerned with sequences A000004 A000007 A000012 A000027 A000035 A000045 A000079 A000203 A000204 A000225 A000244 A000290 A000302 A000351 A000364 A000400 A000420 A000593 A000670 A000984 A001001 A001018 A001019 A001020 A001021 A001022 A001023 A001024 A001025 A001026 A001027 A001029 A001035 A001037 A001157 A001158 A001641 A001642 A001643 A001692 A001693 A001700 A001945 A003462 A004146 A005171 A005809 A006206 A006953 A006954 A007727 A010052 A011557 A014551 A022553 A023890 A027306 A027376 A027377 A027380 A027381 A032164 A032165 A032166 A032167 A032170 A035316 A047863 A048578 A056045 A059928 A059990 A059991 A060164 A060165 A060166 A060167 A060168 A060169 A060170 A060171 A060172 A060173 A060216 A060217 A060218 A060219 A060220 A060221 A060222 A060223 A060224 A060477 A060478 A060479 A060480 .)

Received March 20, 2001. Published in Journal of Integer Sequences, October 14, 2001.

Return to Journal of Integer Sequences home page