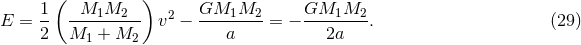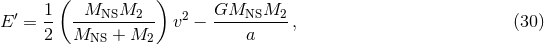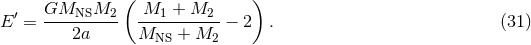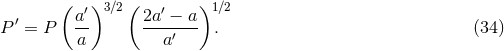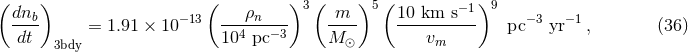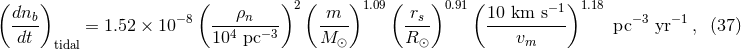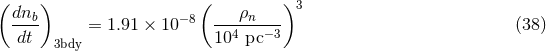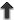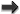4 Relativistic Binaries
We define relativistic binaries to be binary systems containing two degenerate or collapsed objects and an orbital period such that they will be brought into contact within a Hubble time. Note that this definition in intentionally vague and includes binaries which are already in contact as well as systems that will never have relativistic orbital velocities (such as double white dwarfs). Frequently, in the process of becoming a relativistic binary, a binary will exist with a single degenerate or collapse object and a normal star. These systems are tracers of relativistic binaries. Outside of dense stellar clusters, most relativistic binary systems arise from isolated primordial binary systems whose evolution drives them to tight, ultracompact orbits. Dynamical processes in globular clusters can drive wide binary systems toward short orbital periods and can also insert degenerate or collapsed stars into relativistic orbits with other stars. Before addressing specific evolutionary scenarios, we will present the generic features of binary evolution that lead to the formation of relativistic binaries.
4.1 Binary evolution
The evolution of an isolated binary system of two main-sequence stars can significantly affect the evolution
of both component stars if the orbital separation is sufficiently small. For low mass stars (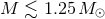 ),
tidal dissipation in the convective envelope will circularize the binary on a time scale given
by
),
tidal dissipation in the convective envelope will circularize the binary on a time scale given
by 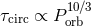 [168, 489, 490]. For such stars, this implies that nearly all binaries with
orbital periods less than 10 days will be circularized by the early main sequence phase. For
high mass stars with radiative envelopes, radiative damping is the dominant mechanism for
circularization. The circularization time scale for high mass stars is
[168, 489, 490]. For such stars, this implies that nearly all binaries with
orbital periods less than 10 days will be circularized by the early main sequence phase. For
high mass stars with radiative envelopes, radiative damping is the dominant mechanism for
circularization. The circularization time scale for high mass stars is 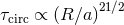 , where
, where 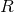 is
the stellar radius and
is
the stellar radius and  is the relative semimajor axis [355]. All high mass binaries with
is the relative semimajor axis [355]. All high mass binaries with
 will be circularized. Both stars start in the main sequence with the mass of the primary
will be circularized. Both stars start in the main sequence with the mass of the primary
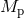 and the mass of the secondary
and the mass of the secondary 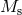 defined, such that
defined, such that 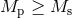 . The binary system is
described by the orbital separation
. The binary system is
described by the orbital separation  , and the mass ratio of the components
, and the mass ratio of the components 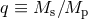 .
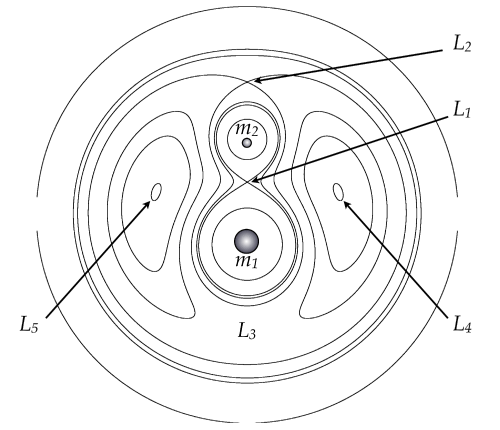
The gravitational potential of the binary system is described by the Roche model where each
star dominates the gravitational potential inside regions called Roche lobes. The two Roche
lobes meet at the inner Lagrange point along the line joining the two stars. Figure 10
.
The gravitational potential of the binary system is described by the Roche model where each
star dominates the gravitational potential inside regions called Roche lobes. The two Roche
lobes meet at the inner Lagrange point along the line joining the two stars. Figure 10 shows
equipotential surfaces in the orbital plane for a binary with
shows
equipotential surfaces in the orbital plane for a binary with 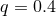 . If the volume of either star
exceeds the effective volume of its Roche lobe, then it is said to fill its Roche lobe. Matter will
stream from a Roche lobe filling star through the inner Lagrange point to the other star in a
process known as Roche lobe overflow (RLOF). This mass transfer affects both the evolution
of the components of the binary as well as the binary properties such as orbital period and
eccentricity.
. If the volume of either star
exceeds the effective volume of its Roche lobe, then it is said to fill its Roche lobe. Matter will
stream from a Roche lobe filling star through the inner Lagrange point to the other star in a
process known as Roche lobe overflow (RLOF). This mass transfer affects both the evolution
of the components of the binary as well as the binary properties such as orbital period and
eccentricity.
Roche lobe overflow can be triggered by the evolution of the binary properties or by evolution of the component stars. On the one hand, the orbital separation of the binary can change so that the Roche lobe can shrink to within the surface of one of the stars. On the other hand, stellar evolution may eventually cause one of the stars to expand and fill its Roche lobe. When both stars in the binary are main-sequence stars, the latter process is more common. Since the more massive star will evolve first, it will be the first to expand and fill its Roche lobe. At this stage, the mass exchange can be conservative (no mass is lost from the binary) or non-conservative (mass is lost). Depending on the details of the mass exchange and the evolutionary stage of the mass-losing star there are several outcomes that will lead to the formation of a relativistic binary. The primary star can lose its envelope, revealing its degenerate core as either a helium, carbon-oxygen, or oxygen-neon white dwarf; it can explode as a supernova, leaving behind a neutron star or a black hole; or it can simply lose mass to the secondary so that they change roles. Barring disruption of the binary, its evolution will then continue. In most outcomes, the secondary is now the more massive of the two stars and it may evolve off the main sequence to fill its Roche lobe. The secondary can then initiate mass transfer or mass loss with the result that the secondary can also become a white dwarf, neutron star, or black hole.
The relativistic binaries that result from this process fall into a number of observable categories. A
WD–MS or WD–WD binary may eventually become a cataclysmic variable once the white
dwarf begins to accrete material from its companion. If the companion is a main-sequence star,
RLOF can be triggered by the evolution of the companion or more commonly by a process
known as magnetic braking. If the companion is a low mass star with a convective envelope
( ) then the binary can lose angular momentum through its wind in a process
proposed by Verbunt and Zwaan [474] in the context of LMXBs. The general mechanism of
magnetic braking involves the removal of large amounts of angular momentum through an
ionized stellar wind that is forced to co-rotate with the magnetic field of the star out to large
distances. Stars with convective envelopes can sustain the enhanced magnetic activity necessary
to support this mechanism. Further details of the magnetic braking process can be found in
Postnov and Yungelson [392] and Knigge, Baraffe, and Patterson [267
) then the binary can lose angular momentum through its wind in a process
proposed by Verbunt and Zwaan [474] in the context of LMXBs. The general mechanism of
magnetic braking involves the removal of large amounts of angular momentum through an
ionized stellar wind that is forced to co-rotate with the magnetic field of the star out to large
distances. Stars with convective envelopes can sustain the enhanced magnetic activity necessary
to support this mechanism. Further details of the magnetic braking process can be found in
Postnov and Yungelson [392] and Knigge, Baraffe, and Patterson [267 ]. If the companion is
another white dwarf, then RLOF is triggered by the gradual shrinking of the orbit through the
emission of gravitational radiation. Some WD–WD cataclysmic variables are also known as
AM CVn stars if they exhibit strong He lines. If the total mass of the WD–WD binary is above the
Chandrasekhar mass (
]. If the companion is
another white dwarf, then RLOF is triggered by the gradual shrinking of the orbit through the
emission of gravitational radiation. Some WD–WD cataclysmic variables are also known as
AM CVn stars if they exhibit strong He lines. If the total mass of the WD–WD binary is above the
Chandrasekhar mass (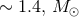 ), the system may be a double degenerate progenitor to a Type Ia
supernova.
), the system may be a double degenerate progenitor to a Type Ia
supernova.
The orbit of a NS–MS or NS–WD binary will shrink due to the emission of gravitational radiation. At
the onset of RLOF, the binary will become either a low-mass X-ray binary (if the donor star has a lower
mass than the accretor, typically a white dwarf or main sequence star with 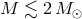 ), or a high-mass
X-ray binary (if the donor is the more massive component). These objects may further evolve to become
millisecond pulsars if the neutron star is spun up during the X-ray binary phase [96
), or a high-mass
X-ray binary (if the donor is the more massive component). These objects may further evolve to become
millisecond pulsars if the neutron star is spun up during the X-ray binary phase [96 , 405
, 405 ]. A NS–NS
binary will remain virtually invisible unless one of the neutron stars is observable as a pulsar. A
BH–MS or BH–WD binary may also become a low- or high-mass X-ray binary. If the neutron star
is observable as a pulsar, a BH–NS binary will appear as a binary pulsar. BH–BH binaries
will be invisible unless they accrete matter from the interstellar medium. A comprehensive
table of close binary types that can be observed in electromagnetic radiation can be found in
Hilditch [215
]. A NS–NS
binary will remain virtually invisible unless one of the neutron stars is observable as a pulsar. A
BH–MS or BH–WD binary may also become a low- or high-mass X-ray binary. If the neutron star
is observable as a pulsar, a BH–NS binary will appear as a binary pulsar. BH–BH binaries
will be invisible unless they accrete matter from the interstellar medium. A comprehensive
table of close binary types that can be observed in electromagnetic radiation can be found in
Hilditch [215 ].
].
The type of binary that emerges depends upon the orbital separation and the masses of the component
stars. During the evolution of a 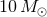 star, the radius will slowly increase by a factor of about two as the
star progresses from zero age main sequence to terminal age main sequence. The radius will then increase by
about another factor of 50 as the star transitions to the red giant phase, and an additional factor of 10
during the transition to the red supergiant phase. These last two increases in size occur very quickly
compared with the slow increase during the main-sequence evolution [372
star, the radius will slowly increase by a factor of about two as the
star progresses from zero age main sequence to terminal age main sequence. The radius will then increase by
about another factor of 50 as the star transitions to the red giant phase, and an additional factor of 10
during the transition to the red supergiant phase. These last two increases in size occur very quickly
compared with the slow increase during the main-sequence evolution [372 ]. Depending upon the orbital
separation, the onset of RLOF can occur any time during the evolution of the star. Mass transfer can be
divided into three cases related to the timing of the onset of RLOF (see Hilditch [215] for more
details):
]. Depending upon the orbital
separation, the onset of RLOF can occur any time during the evolution of the star. Mass transfer can be
divided into three cases related to the timing of the onset of RLOF (see Hilditch [215] for more
details):
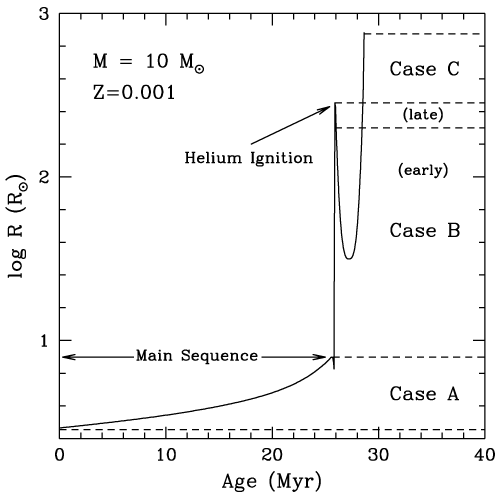
Case A: If the orbital separation is small enough (such that the period is usually a few days), the star can fill its Roche lobe during its slow expansion through the main-sequence phase while still burning hydrogen in its core.
Case B: If the orbital period is less than about 100 days, but longer than a few days, the star will fill its Roche lobe during the rapid expansion to a red giant with a helium core. If the helium core ignites during this phase and the transfer is interrupted, the mass transfer is case BB.
Case C: If the orbital period is above 100 days, the star can evolve to the red supergiant
phase before it fills its Roche lobe. In this case, the star may have a CO or ONe core.
The typical evolution of the radius for a low metallicity star is shown in Figure 11 . Case A mass transfer
occurs during the slow growth, Case B during the first rapid expansion, and Case C during the final
expansion phase. The nature of the remnant depends upon the state of the primary during the onset of
RLOF and the orbital properties of the resultant binary depend upon the details of the mass
transfer.
. Case A mass transfer
occurs during the slow growth, Case B during the first rapid expansion, and Case C during the final
expansion phase. The nature of the remnant depends upon the state of the primary during the onset of
RLOF and the orbital properties of the resultant binary depend upon the details of the mass
transfer.
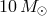 star with a metallicity of Z = 0.001. Image
reproduced by permission from Pfahl et al. [372
star with a metallicity of Z = 0.001. Image
reproduced by permission from Pfahl et al. [372 ], copyright by IOP.
], copyright by IOP.4.2 Mass transfer
Although there are still many unanswered theoretical questions about the nature of the mass transfer phase, the basic properties of the evolution of a binary due to mass transfer can easily be described. The rate at which a star can adjust to changes in its mass is governed by three time scales. The dynamical time scale results from the adiabatic response of the star to restore hydrostatic equilibrium, and can be approximated by the free fall time across the radius of the star,
where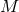 and
and 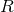 are the mass and radius of the star. The thermal equilibrium of the star is restored
over a longer period given by the thermal time scale
where
are the mass and radius of the star. The thermal equilibrium of the star is restored
over a longer period given by the thermal time scale
where 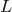 is the luminosity of the star. Finally, the main-sequence lifetime of the star itself provides a third
time scale, which is also known as the nuclear time scale:
is the luminosity of the star. Finally, the main-sequence lifetime of the star itself provides a third
time scale, which is also known as the nuclear time scale:
The rate of mass transfer/loss from the Roche lobe filling star is governed by how the star’s radius
changes in response to changes in its mass. Hjellming and Webbink [221] describe these changes and the
response of the Roche lobe to mass changes in the binary using the radius-mass exponents,
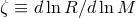 , for each of the three processes described in Eqs. (20
, for each of the three processes described in Eqs. (20 , 21
, 21 , 22
, 22 ) and defining
) and defining
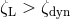 , the star cannot adjust to the Roche lobe, then the
mass transfer takes place on a dynamical time scale and is limited only by the rate at which material can
stream through the inner Lagrange point. If
, the star cannot adjust to the Roche lobe, then the
mass transfer takes place on a dynamical time scale and is limited only by the rate at which material can
stream through the inner Lagrange point. If 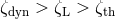 , then the mass transfer rate is governed by
the slow expansion of the star as it relaxes toward thermal equilibrium, and it occurs on a thermal time
scale. If both
, then the mass transfer rate is governed by
the slow expansion of the star as it relaxes toward thermal equilibrium, and it occurs on a thermal time
scale. If both 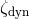 and
and 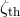 are greater than
are greater than 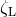 , then the mass loss is driven either by stellar evolution
processes or by the gradual shrinkage of the orbit due to the emission of gravitational radiation. The time
scale for both of these processes is comparable to the nuclear time scale. A good analysis of mass
transfer in cataclysmic variables can be found in King et al. [263] and Knigge, Baraffe, and
Patterson [267].
, then the mass loss is driven either by stellar evolution
processes or by the gradual shrinkage of the orbit due to the emission of gravitational radiation. The time
scale for both of these processes is comparable to the nuclear time scale. A good analysis of mass
transfer in cataclysmic variables can be found in King et al. [263] and Knigge, Baraffe, and
Patterson [267].
Conservative mass transfer occurs when there is no mass loss from the system, and therefore all mass
lost from one star is accreted by the other star. During conservative mass transfer, the orbital elements of
the binary can change. Consider a system with total mass 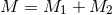 and semi-major axis
and semi-major axis  . The
total orbital angular momentum
. The
total orbital angular momentum
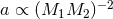 . Using Kepler’s third law and denoting the initial values by
a subscript
. Using Kepler’s third law and denoting the initial values by
a subscript 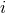 , we find:
Differentiating Eq. (25
, we find:
Differentiating Eq. (25 ) and noting that conservative mass transfer requires
) and noting that conservative mass transfer requires 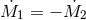 gives:
Note that if the more massive star loses mass, then the orbital period decreases and the orbit shrinks. If the
less massive star is the donor, then the orbit expands. Usually, the initial phase of RLOF takes place as the
more massive star evolves. As a consequence, the orbit of the binary will shrink, driving the binary to a
more compact orbit.
gives:
Note that if the more massive star loses mass, then the orbital period decreases and the orbit shrinks. If the
less massive star is the donor, then the orbit expands. Usually, the initial phase of RLOF takes place as the
more massive star evolves. As a consequence, the orbit of the binary will shrink, driving the binary to a
more compact orbit.
In non-conservative mass transfer, both mass and angular momentum can be removed from the system. There are two basic non-conservative processes that are important for the formation of relativistic binaries – the common-envelope process and the supernova explosion of one component of the binary. The result of the first process is often a short-period, circularized binary containing a white dwarf. Although the most common outcome of the second process is the disruption of the binary, occasionally this process will result in an eccentric binary containing a neutron star or a black hole.
Common envelope scenarios result when one component of the binary expands so rapidly that the mass transfer is unstable and the companion becomes engulfed by the donor star. This can happen if the mass transfer rate is so great that it exceeds the Eddington mass accretion rate of the accretor, or when the donor expands past the outer Lagrange point [361, 481]. The companion can then mechanically eject the envelope of the donor star. There are two proposed approaches to determining the outcome of the process of ejection of the envelope.
The most commonly used approach is the “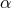 -prescription” of Webbink [482
-prescription” of Webbink [482 ], in which the energy
required to eject the envelope comes from the orbital energy of the binary and thus the orbit shrinks. The
efficiency of this process determines the final orbital period after the common envelope phase. This is
described by the efficiency parameter
], in which the energy
required to eject the envelope comes from the orbital energy of the binary and thus the orbit shrinks. The
efficiency of this process determines the final orbital period after the common envelope phase. This is
described by the efficiency parameter
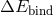 is the binding energy of the mass stripped from the envelope and
is the binding energy of the mass stripped from the envelope and 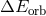 is the change in
the orbital energy of the binary. The result of the process is the exposed degenerate core of the donor star in
a tight, circular orbit with the companion. This process can result in a double degenerate binary if the
process is repeated twice or if the companion has already evolved to a white dwarf through some
other process such as standard stellar evolution. If enough orbital energy is lost it can also
lead to a merger of the binary components. A brief description of the process is outlined by
Webbink [482], and a discussion of the factors involved in determining
is the change in
the orbital energy of the binary. The result of the process is the exposed degenerate core of the donor star in
a tight, circular orbit with the companion. This process can result in a double degenerate binary if the
process is repeated twice or if the companion has already evolved to a white dwarf through some
other process such as standard stellar evolution. If enough orbital energy is lost it can also
lead to a merger of the binary components. A brief description of the process is outlined by
Webbink [482], and a discussion of the factors involved in determining 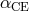 is presented in Sandquist et
al. [417].
is presented in Sandquist et
al. [417].
The other approach that has been suggested is the “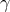 -prescription” of Nelemans et al. [351].
In this approach, other energy sources such as tidal heating or luminosity of the donor may
assist in the unbinding of the envelope. The material lost by the envelope is assumed to carry
away angular momentum and reduce the total angular momentum of the system, such that:
-prescription” of Nelemans et al. [351].
In this approach, other energy sources such as tidal heating or luminosity of the donor may
assist in the unbinding of the envelope. The material lost by the envelope is assumed to carry
away angular momentum and reduce the total angular momentum of the system, such that:
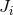 and
and 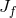 are the initial and final angular momenta of the binary,
are the initial and final angular momenta of the binary, 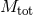 is the total mass
of the binary prior to mass loss, and
is the total mass
of the binary prior to mass loss, and 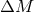 is the mass lost in the ejection of the envelope.
For most reasonable models of post common envelope binaries, the value of
is the mass lost in the ejection of the envelope.
For most reasonable models of post common envelope binaries, the value of 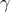 was found
to lie in the range of
was found
to lie in the range of 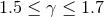 and this was interpreted to mean that
and this was interpreted to mean that 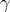 was a more
constrained parameter to determine outcome of a common envelope phase. Recently, however,
Webbink showed that for reasonable initial and final masses,
was a more
constrained parameter to determine outcome of a common envelope phase. Recently, however,
Webbink showed that for reasonable initial and final masses, 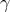 will lie within this range if
the angular momentum loss is required to lie between the minimum given by the Jeans mode
mass loss and total loss of angular momentum of the system [483]. This has been borne out by
observation [494].
will lie within this range if
the angular momentum loss is required to lie between the minimum given by the Jeans mode
mass loss and total loss of angular momentum of the system [483]. This has been borne out by
observation [494].
The effect on a binary of mass loss due to a supernova can be quite drastic. Following Padmanabhan [363],
this process is outlined using the example of a binary in a circular orbit with a semi-major axis  . Let
. Let  be the velocity of one component of the binary relative to the other component. The initial energy of the
binary is given by
be the velocity of one component of the binary relative to the other component. The initial energy of the
binary is given by
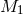 , the expanding mass shell will quickly cross the orbit of
, the expanding mass shell will quickly cross the orbit of  ,
decreasing the gravitational force acting on the secondary. The new energy of the binary is then
where
,
decreasing the gravitational force acting on the secondary. The new energy of the binary is then
where 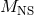 is the mass of the remnant neutron star. We have assumed here that the passage of the mass
shell by the secondary has negligible effect on its velocity (a safe assumption, see Pfahl et al. [372
is the mass of the remnant neutron star. We have assumed here that the passage of the mass
shell by the secondary has negligible effect on its velocity (a safe assumption, see Pfahl et al. [372 ] for a
discussion), and that the primary has received no kick from the supernova (not necessarily a
safe assumption, but see Davies and Hansen [96
] for a
discussion), and that the primary has received no kick from the supernova (not necessarily a
safe assumption, but see Davies and Hansen [96 ] or Pfahl et al. [373] for an application to
globular cluster binaries). Since we have assumed that the instantaneous velocities of both
components have not been affected, we can replace them by
] or Pfahl et al. [373] for an application to
globular cluster binaries). Since we have assumed that the instantaneous velocities of both
components have not been affected, we can replace them by 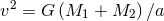 , and so
Note that the final energy will be positive and the binary will be disrupted if
, and so
Note that the final energy will be positive and the binary will be disrupted if 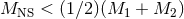 .
This condition occurs when the mass ejected from the system is greater than half of the initial total mass,
where
.
This condition occurs when the mass ejected from the system is greater than half of the initial total mass,
where 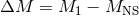 . If the binary is not disrupted, the new orbit becomes eccentric and expands to a
new semi-major axis given by
and orbital period
Note that we have not included any mention of the expected velocity kick that newly born neutron star or
black hole will receive due to asymmetries in the supernova explosion. These kicks can be quite substantial,
up to several hundred kilometers per second and, at least for observed pulsars, seem to be drawn from a
Maxwellian distribution with a peak at 265 km s–1 [222]. In most cases, the kick will further increase the
likelihood that the binary will become unbound, but occasionally the kick velocity will be favorably oriented
and the binary will remain intact. If the kick is higher than the escape velocity of the cluster
(typically less than 50 km s–1), it will also remove the remnant from the system. This mechanism
may be very important in depleting the numbers of neutron stars and black holes in globular
clusters.
. If the binary is not disrupted, the new orbit becomes eccentric and expands to a
new semi-major axis given by
and orbital period
Note that we have not included any mention of the expected velocity kick that newly born neutron star or
black hole will receive due to asymmetries in the supernova explosion. These kicks can be quite substantial,
up to several hundred kilometers per second and, at least for observed pulsars, seem to be drawn from a
Maxwellian distribution with a peak at 265 km s–1 [222]. In most cases, the kick will further increase the
likelihood that the binary will become unbound, but occasionally the kick velocity will be favorably oriented
and the binary will remain intact. If the kick is higher than the escape velocity of the cluster
(typically less than 50 km s–1), it will also remove the remnant from the system. This mechanism
may be very important in depleting the numbers of neutron stars and black holes in globular
clusters.
We have seen that conservative mass transfer can result in a tighter binary if the more massive star is the donor. Non-conservative mass transfer can also drive the components of a binary together during a common envelope phase when mass and angular momentum are lost from the system. Direct mass loss through a supernova explosion can also alter the properties of a binary, but this process generally drives the system toward larger orbital separation and can disrupt the binary entirely. With this exception, the important result of all of these processes is the generation of tight binaries with at least one degenerate object.
The processes discussed so far apply to the generation of relativistic binaries anywhere. They occur
whenever the orbital separation of a progenitor binary is sufficiently small to allow for mass transfer or
common envelope evolution. Population distributions for relativistic binaries are derived from an initial
mass function, a distribution in mass ratios, and a distribution in binary separations. These
initial distributions are then fed into models for binary evolution, such as StarTrack [46] or
SeBa [391, 352 ] in order to determine rates of production of relativistic binaries. The evolution of the
binary is often determined by the application of some simple operational formulae, such as
those described by Tout et al. [462] or Hurley et al. [230
] in order to determine rates of production of relativistic binaries. The evolution of the
binary is often determined by the application of some simple operational formulae, such as
those described by Tout et al. [462] or Hurley et al. [230 ]. For example, Hils, Bender, and
Webbink [220] estimated a population of close white dwarf binaries in the disk of the galaxy
using a Salpeter mass function, a mass ratio distribution strongly peaked at 1, and a separation
distribution that was flat in
]. For example, Hils, Bender, and
Webbink [220] estimated a population of close white dwarf binaries in the disk of the galaxy
using a Salpeter mass function, a mass ratio distribution strongly peaked at 1, and a separation
distribution that was flat in 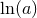 . Other estimates of relativistic binaries differ mostly by
using different distributions [45, 242, 352, 350]. Because of the uncertainties in the form of
the initial distributions, results from these simulations can differ by an order of magnitude or
more.
. Other estimates of relativistic binaries differ mostly by
using different distributions [45, 242, 352, 350]. Because of the uncertainties in the form of
the initial distributions, results from these simulations can differ by an order of magnitude or
more.
4.3 Globular cluster processes
In the galactic field stellar densities are low enough that stars and binaries rarely encounter each other. In this environment binaries evolve in isolation with their properties and fate determined solely by their initial conditions and the processes described in Sections 4.1 and 4.2. In star clusters, stellar densities are much higher and close encounters between stars and binaries are common. Such encounters can affect a binary’s parameters and dramatically alter the evolution that would otherwise occur if the same binary were isolated. Some outcomes that are of particular interest for relativistic binaries include:
- Reduction or increase of the period during distant encounters.
- Exchange interactions where binary membership is changed in close encounters.
- Binary formation during strong few-body interactions.
- Encounter-induced binary mergers.
Different types of interactions can produce these outcomes and we briefly describe the most important in the terms normally used by stellar dynamicists – the number of bodies and type of objects involved in the interaction. In all cases these interactions must be distinguished from the distant, weak interactions that drive two-body relaxation of clusters as described in Section 2.3. The interactions affecting binary parameters result from close encounters, the outcomes of which cannot be described statistically using the language of relaxation theory. Note also that the term binding energy is normally spoken of as though it were a positive quantity. Thus binaries with the largest (most negative) binding energy are the most tightly bound.
4.3.1 Single-single interactions
As the name suggests, single-single interactions are encounters between two individual stars. If the periastron of the encounter is sufficiently small, the stars may excite tidal oscillations in each other at the cost of some of their relative kinetic energies. If sufficient kinetic energy is dissipated, the stars can become bound and form a new binary.
The exact nature of the oscillations excited in the stars is not important, only that they dissipate sufficient kinetic energy. Furthermore, to obtain a bound orbit it is only necessary to dissipate sufficient kinetic energy that the total energy at apocenter is reduced to less than zero. The basic condition for tidal capture is:
where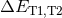 is the energy associated with the tidal oscillation in each star,
is the energy associated with the tidal oscillation in each star, 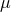 is the reduced mass,
and
is the reduced mass,
and 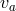 is the relative velocity at apocenter (or infinity) [121
is the relative velocity at apocenter (or infinity) [121 ]. Only a fraction
]. Only a fraction  , where
, where 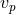 is
the velocity at pericenter, of the energy must be converted to tidal oscillations in order for a
capture to occur. For example, an encounter with a pericenter velocity of
is
the velocity at pericenter, of the energy must be converted to tidal oscillations in order for a
capture to occur. For example, an encounter with a pericenter velocity of 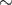 100 km s–1 in a
cluster with a velocity dispersion of
100 km s–1 in a
cluster with a velocity dispersion of 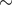 10 km s–1 only needs to dissipate
10 km s–1 only needs to dissipate 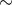 1% of the
apocenter kinetic energy in order for a capture to occur. This mechanism favours the creation of
binaries in encounters with large ratios between apocenter and pericenter velocity. Thus it
tends to produce highly eccentric binaries with very small pericenter separations. These binaries
will circularize over time due to continued excitation of tidal oscillations during the pericenter
passages.
1% of the
apocenter kinetic energy in order for a capture to occur. This mechanism favours the creation of
binaries in encounters with large ratios between apocenter and pericenter velocity. Thus it
tends to produce highly eccentric binaries with very small pericenter separations. These binaries
will circularize over time due to continued excitation of tidal oscillations during the pericenter
passages.
This process was once thought to be the dominant path for dynamically creating binaries in star
clusters [121 , 57
, 57 ] since two-body interactions are more likely than higher-order encounters [443
] since two-body interactions are more likely than higher-order encounters [443 ]. Giant
stars are the most likely to tidally capture a companion because their large radii give them
a large cross section for interactions and their low densities make exciting tidal oscillations
relatively easy. In particular binaries of neutron stars with degenerate companions were though
to originate from the capture of the neutron star by a red giant [121
]. Giant
stars are the most likely to tidally capture a companion because their large radii give them
a large cross section for interactions and their low densities make exciting tidal oscillations
relatively easy. In particular binaries of neutron stars with degenerate companions were though
to originate from the capture of the neutron star by a red giant [121 ]. It has been realized,
however, that tidalcapture binaries may be rare because even giant stars must approach very
closely, to within a few stellar radii, in order for tidal oscillations to dissipate enough energy for a
capture to occur [121
]. It has been realized,
however, that tidalcapture binaries may be rare because even giant stars must approach very
closely, to within a few stellar radii, in order for tidal oscillations to dissipate enough energy for a
capture to occur [121 , 290, 393]. In these situations it is more likely that, depending upon the
exact stellar equation of state, tidal capture events more commonly lead to a merger than a
binary [407
, 290, 393]. In these situations it is more likely that, depending upon the
exact stellar equation of state, tidal capture events more commonly lead to a merger than a
binary [407 , 324
, 324 , 24, 241, 405
, 24, 241, 405 ]. Because of the difficulty of exciting tidal oscillations in degenerate matter,
forming a compact binary directly by tidal capture between two compact objects is highly
unlikely.
]. Because of the difficulty of exciting tidal oscillations in degenerate matter,
forming a compact binary directly by tidal capture between two compact objects is highly
unlikely.
4.3.2 Three-body interactions
During a close three-body encounter it is possible for one of the stars to gain kinetic energy and, if the
relative kinetic energy of the remaining two stars is sufficiently reduced, they can form a bound pair. In
general the least massive body will gain the highest velocity, since it is the easiest to accelerate, and the two
more massive bodies will remain (this can also be seen as a consequence of energy equipartition).
Heggie [196 ] showed that if
] showed that if 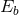 is the binding energy of the new binary, the rate of three-body binary
formation is
is the binding energy of the new binary, the rate of three-body binary
formation is 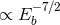 . Thus three-body interactions tend to favour the creation of binaries with low
binding energies. The binding energy can be increased by later encounters (see Section 4.3.3). For the
case of an interaction where all stars have the same mass there is about a 10% probability
that a binary formed by three-body interactions will gain sufficient binding energy to survive
permanently [170
. Thus three-body interactions tend to favour the creation of binaries with low
binding energies. The binding energy can be increased by later encounters (see Section 4.3.3). For the
case of an interaction where all stars have the same mass there is about a 10% probability
that a binary formed by three-body interactions will gain sufficient binding energy to survive
permanently [170 , 443
, 443 ].
].
Three-body binary formation interactions are less common than tidal interactions because the
probability of a close encounter between three stars is smaller than the probability of an encounter between
two. Therefore stellar densities need to be higher for three-body binary formation to be efficient than they
do for tidal interactions [170 , 235
, 235 , 443
, 443 ]. For the case of equal masses Spitzer [443
]. For the case of equal masses Spitzer [443 ] estimates a three-body
binary formation rate of
] estimates a three-body
binary formation rate of
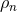 is the number density of stars,
is the number density of stars, 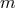 is their mass and
is their mass and 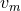 is the three dimensional RMS
random velocity. By contrast the rate of formation due to tidal capture in the same system (assuming a
polytropic stellar equation of state with
is the three dimensional RMS
random velocity. By contrast the rate of formation due to tidal capture in the same system (assuming a
polytropic stellar equation of state with 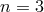 ) is
) is
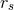 is the radius of the stars. For
is the radius of the stars. For  and
and 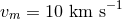 it is clear that the rate of binary
formation by tidal capture is much higher at low
it is clear that the rate of binary
formation by tidal capture is much higher at low  and that three-body binary formation only begins to
dominate at
and that three-body binary formation only begins to
dominate at 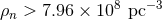 , a density higher than that found in most globular clusters. However,
thanks to the strong scaling with mass, three-body binary formation becomes much more important for
more massive stars. For the same
, a density higher than that found in most globular clusters. However,
thanks to the strong scaling with mass, three-body binary formation becomes much more important for
more massive stars. For the same 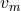 but with
but with 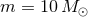 and assuming
and assuming 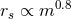 then
while
and three-body interactions begin to dominate at
then
while
and three-body interactions begin to dominate at 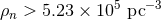 , much closer to the densities
found in the cores of Galactic globular clusters. Because it is not necessary to excite tides during three-body
interactions, pericenter passages need not be as close in order to form binaries so mergers are a less common
outcome than they are for tidal interactions. Furthermore, because it is not necessary to excite tidal
oscillations, it is possible for three-body interactions to form compact binaries directly from degenerate
objects. It is worth noting that, in equal-mass systems, neither tidal nor three-body interactions are likely
to produce many binaries over the lifetime of a star cluster [235
, much closer to the densities
found in the cores of Galactic globular clusters. Because it is not necessary to excite tides during three-body
interactions, pericenter passages need not be as close in order to form binaries so mergers are a less common
outcome than they are for tidal interactions. Furthermore, because it is not necessary to excite tidal
oscillations, it is possible for three-body interactions to form compact binaries directly from degenerate
objects. It is worth noting that, in equal-mass systems, neither tidal nor three-body interactions are likely
to produce many binaries over the lifetime of a star cluster [235 , 170, 57
, 170, 57 , 443
, 443 , 244
, 244 ]. For a
system with a mass function the situation may be slightly different. Ivanova et al. showed that
while the formation rate of binaries due to three-body interactions is negligable for solar-mass
stars, for more massive stars the rate could be much higher [244
]. For a
system with a mass function the situation may be slightly different. Ivanova et al. showed that
while the formation rate of binaries due to three-body interactions is negligable for solar-mass
stars, for more massive stars the rate could be much higher [244 , 245
, 245 ]. In particular, Ivanova et
al. (2010) [245
]. In particular, Ivanova et
al. (2010) [245 ] showed that for very large mass ratios three-body binary formation could be
important for forming certain types of compact binaries. Nevertheless, primordial binaries and the
interactions involving them are critical for producing large numbers of relativistic binaries in globular
clusters.
] showed that for very large mass ratios three-body binary formation could be
important for forming certain types of compact binaries. Nevertheless, primordial binaries and the
interactions involving them are critical for producing large numbers of relativistic binaries in globular
clusters.
4.3.3 Binary-single interactions
Binary-single interactions, although formally still three-body interactions, differ because two of the stars are already bound. Several outcomes are possible in such an encounter depending on the relative kinetic energy of the star and binary and on the binding energy of the binary itself.
If the kinetic energy of the star is less than the binding energy of the binary, energy equipartition
requires that the star accelerate and the binding energy of the binary increase (the period will become
shorter). If, however, the kinetic energy of the star is greater than the binding energy of the binary, the star
will donate kinetic energy to the binary and the binding energy will decrease (the period will become
longer). For equal-mass systems this introduces a simple yet important classification for binaries. If
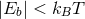 (Section 2.3) then the binary is said to be “soft” and, on average, will tend to have its period
increased by encounters (softening). If
(Section 2.3) then the binary is said to be “soft” and, on average, will tend to have its period
increased by encounters (softening). If  than the binary is said to be “hard” and will
tend to have its period decreased by encounters (hardening). Assuming a Maxwellian velocity
distribution, a hard binary gains on average
than the binary is said to be “hard” and will
tend to have its period decreased by encounters (hardening). Assuming a Maxwellian velocity
distribution, a hard binary gains on average 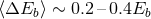 per interaction [196
per interaction [196 , 239]
(although this is only fully valid in the case of very hard binaries [235]). Since the encounter rate is
proportional to the semi-major axis of the binary (
, 239]
(although this is only fully valid in the case of very hard binaries [235]). Since the encounter rate is
proportional to the semi-major axis of the binary (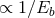 ), the energy of a hard binary increases by
), the energy of a hard binary increases by
 per relaxation time [57
per relaxation time [57 ]. This leads to the “Heggie–Hills Law” [196, 216]
that states “hard binaries get harder while soft binaries get softer”. The end result of binary
hardening can be a merger while the end result of binary softening can be the disruption of the
binary.
]. This leads to the “Heggie–Hills Law” [196, 216]
that states “hard binaries get harder while soft binaries get softer”. The end result of binary
hardening can be a merger while the end result of binary softening can be the disruption of the
binary.
In a multi-mass system the division between hard and soft binaries is not so clear since the relative
energies depend upon the specific masses of all the bodies involved. For an individual encounter between a
binary with member masses 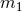 and
and  and a single star of mass
and a single star of mass 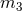 travelling at velocity
travelling at velocity  , it is
possible to define a critical velocity [237]:
, it is
possible to define a critical velocity [237]:
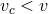 the binary cannot capture the single star and the star can disrupt the binary
(softening) and for
the binary cannot capture the single star and the star can disrupt the binary
(softening) and for 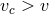 then the binary can capture the single star and cannot be disrupted in the
process (hardening). Thus the distinction between hard and soft binaries still exists in multi-mass systems.
It has been shown by Hills that it is also possible to use the ratio of orbital speeds to define whether the
binary will gain or lose energy [218].
then the binary can capture the single star and cannot be disrupted in the
process (hardening). Thus the distinction between hard and soft binaries still exists in multi-mass systems.
It has been shown by Hills that it is also possible to use the ratio of orbital speeds to define whether the
binary will gain or lose energy [218].
The reference to capture alludes to another important process that can occur in binary-single
interactions: exchange. In an exchange interaction one of the original binary members is replaced by the
single star so the binary membership changes. As with other encounters, equipartition of energy favours the
ejection of the lowest-mass object and exchange encounters are a way of introducing massive objects into
binaries. It has been shown that in the limit of  or
or 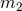 , the probability for a massive object to
be exchanged into the binary is
, the probability for a massive object to
be exchanged into the binary is 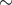 1 [219]. Thus it is possible to create a compact binary from a
binary where neither member was originally massive enough to become a compact object. This
may be particularly effective for BHs since they are the most massive objects in evolved star
clusters [436
1 [219]. Thus it is possible to create a compact binary from a
binary where neither member was originally massive enough to become a compact object. This
may be particularly effective for BHs since they are the most massive objects in evolved star
clusters [436 ].
].
4.3.4 Binary-binary interactions
There are many possible outcomes for binary-binary interactions, especially in multi-mass systems, and they
depend rather sensitively upon the initial conditions of the encounter. Therefore a quantitative theory of
these interactions is lacking. For sufficiently distant encounters both binaries will “see” each other as single
centers of mass and a hardening or softening interaction will occur in both binaries. There are also some
general results for close encounters where all stars have equal mass. If one of the binaries is much harder
than the other, it can be exchanged into the other binary as a single star. This produces a hierarchical
three-body system, the future of which will be decided by further interactions [443 ]. One or both binaries
can also be disrupted during the encounter. Numerical experiments show that at least one of the binaries is
disrupted in
]. One or both binaries
can also be disrupted during the encounter. Numerical experiments show that at least one of the binaries is
disrupted in 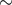 88% of cases [329, 330, 331, 144
88% of cases [329, 330, 331, 144 ]. It is also possible for one or, more rarely, both
binaries to exchange members with each other. Thus binary-binary interactions can provide all
of the effects of binary-single interactions but can result in extensive binary destruction as
well.
]. It is also possible for one or, more rarely, both
binaries to exchange members with each other. Thus binary-binary interactions can provide all
of the effects of binary-single interactions but can result in extensive binary destruction as
well.
Higher-order interactions (those involving more than four bodies) are also possible but will be quite rare
and are even less amenable to general quantitative analysis than are binary-binary encounters. Because
binaries with small semi-major axes have a small interaction cross section, the majority of these encounters
affect the binary while it is still quite wide by relativistic standards. Therefore it is unlikely to have a
three-body (or higher-order) interaction while a binary is in the gravitational wave emission regime so
globular clusters dynamics do not make it necessary to calculate merger waveforms perturbed by a third
body [14 ].
].

![[ ]1∕2 ( 2R3 )1 ∕2 ( R )3 M ⊙ tdyn ≃ ----- ∼ 40 ---- ---- min, (20 ) GM R ⊙ M](article194x.gif)
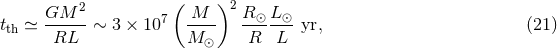


![[ 2 2 ]1∕2 J = GM--1M-2a- (24 ) M](article209x.gif)
![[ ] P-- M1iM2i--3 P = M M . (25 ) i 1 2](article212x.gif)