12 Further Contributions from the United States
12.1 Eisenhart in Princeton
While Einstein pursued his research in UFT along the lines of mixed geometry at the Institute for Advanced
Studies of Princeton, NJ, his colleague in the mathematics department of Princeton University,
L. P. Eisenhart, kept quiet until the beginning of the 1950s. He had written a book on Non-Riemannian
Geometry in 1927 [182*], and since the twenties had had a long-standing interest in teleparallelism and UFT
(cf. Section 6.4 of Part I and [181]). Being three years older than Einstein he had retired in 1945.
Nevertheless, in the 1950s he wrote three further papers about UFT. He first introduced a non-symmetric
metric 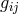 and a non-symmetric connection [184] in 1951. Unlike Einstein, whose papers he
did not refer to, Eisenhart did not take the connection
and a non-symmetric connection [184] in 1951. Unlike Einstein, whose papers he
did not refer to, Eisenhart did not take the connection 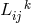 as an independent variable but
built it entirely from the metric tensor and its first derivatives such as the Japanese physicist
K. Hattori248
had done in the 1920s [240*]:
as an independent variable but
built it entirely from the metric tensor and its first derivatives such as the Japanese physicist
K. Hattori248
had done in the 1920s [240*]:
 is an arbitrary tensor. In fact, Eisenhart’s
is an arbitrary tensor. In fact, Eisenhart’s 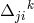 is exactly the same as Hattori’s connection
is exactly the same as Hattori’s connection
![gρν ∗[μ λ,ρ]](article2321x.gif) ([240], Eq. (1.6), p. 540). The tensor to be added was chosen by Eisenhart to be (indices are
moved with the symmetric part of the metric):
From (433*) we notice that
where the Christoffel symbol is formed with the symmetric part of the metric. The torsion tensor is given
by:
Eisenhart used the curvature tensor
([240], Eq. (1.6), p. 540). The tensor to be added was chosen by Eisenhart to be (indices are
moved with the symmetric part of the metric):
From (433*) we notice that
where the Christoffel symbol is formed with the symmetric part of the metric. The torsion tensor is given
by:
Eisenhart used the curvature tensor 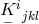 and its contraction
and its contraction  After some manipulations, he obtained
an equation for the Ricci tensor formed from
After some manipulations, he obtained
an equation for the Ricci tensor formed from  which is contained already in Hattori’s paper (Eisenhart’s
Eq. (26)).249
Eisenhart’s paper dealt only with differential geometry; no physical motivation or interpretation were given.
This applies also to a subsequent publication in which, after formal manipulations, several
expressions for possible curvature tensors and Einstein’s Hermitian-symmetrized Ricci tensor (196*)
were derived [185]. The 3rd edition of Einstein’s Meaning of Relativity [150] now was referred
to.
which is contained already in Hattori’s paper (Eisenhart’s
Eq. (26)).249
Eisenhart’s paper dealt only with differential geometry; no physical motivation or interpretation were given.
This applies also to a subsequent publication in which, after formal manipulations, several
expressions for possible curvature tensors and Einstein’s Hermitian-symmetrized Ricci tensor (196*)
were derived [185]. The 3rd edition of Einstein’s Meaning of Relativity [150] now was referred
to.
Eisenhart’s second attempt, after the death of Einstein, presented a new unified theory of gravitation
and electromagnetism within metric-affine geometry [186*, 187*, 188*], and [189*]. Although in a different
geometrical setting, eventually the theory formally led to the Einstein–Maxwell field equations in
Riemannian geometry. The main difference to Einstein’s approach was that Eisenhart kept the metric tensor
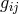 symmetric while embedding the electromagnetic field tensor
symmetric while embedding the electromagnetic field tensor 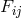 into the connection by an ad-hoc
ansatz [186]:
into the connection by an ad-hoc
ansatz [186]:
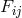 is derived from a 4-potential and supposed to satisfy
is derived from a 4-potential and supposed to satisfy
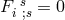 .250
Thus, vector torsion does vanish. In the first paper, Eisenhart’s field equations were:
With his ansatz (437*), the equation for the auto-parallels of the connection
.250
Thus, vector torsion does vanish. In the first paper, Eisenhart’s field equations were:
With his ansatz (437*), the equation for the auto-parallels of the connection  read as:
These results were unphysical. Four months later, Eisenhart tried to find a remedy by postulating [187]:
with
read as:
These results were unphysical. Four months later, Eisenhart tried to find a remedy by postulating [187]:
with 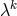 satisfying
All he arrived at was the field equation
satisfying
All he arrived at was the field equation 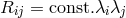 . A slight generalization of (441*):
did not help much. Because he did not use a variational principle, Eisenhart always had to build his theories
such that an identity in Riemannian geometry was guaranteed: the vanishing of the divergence of the
Einstein tensor.
. A slight generalization of (441*):
did not help much. Because he did not use a variational principle, Eisenhart always had to build his theories
such that an identity in Riemannian geometry was guaranteed: the vanishing of the divergence of the
Einstein tensor.
Again two months later, in his 3rd installment, Eisenhart finally arrived at the Einstein–Maxwell equation of general relativity [188*]. This time, the ansatz (440*) with (441*) was changed substantially into:
This equation is interesting because the energy-momentum tensor of the electromagnetic field is built directly into the connection (curvature). Eisenhart was aware that the Einstein–Maxwell equations did not represent the union of the gravitational and electromagnetic field aimed at. He quoted Einstein as saying that “A theory in which the gravitational field and electromagnetic field do not enter as logically distinct structures would be much preferable.” ([188], p. 881.) This quotation was repeated in the last of this sequence of papers by Eisenhart, in which “the final result of my third paper” were derived “in a somewhat different manner.” ([189], p. 333.)In his last contribution to UFT, when he was 83 years old, Eisenhart returned to mixed geometry [190]. Starting from Einstein’s condition (200*) on the metric, he aimed at solving it for the connection as a function of the metric and its first derivatives. Unaware of the solutions given previously (cf. Section 10.2.3), he achieved this only with the help of the additional constraint for torsion:
From this, again the vanishing of vector torsion follows. In this special case, from (444*) with the notation of (3*), (4*), Eisenhart’s solution is given by: Seen in context, Eisenhart’s papers on UFT from the 1950s did bring neither a new development in geometry nor an advance for physics. Cf. also the paper by Horvath [285*] in Section 15.1.
12.2 Hlavatý at Indiana University
Hlavatý is the fourth of the main figures in UFT besides Einstein, Schrödinger, and Tonnelat. His research was published first in a sizeable number of articles in the Journal of Rational Mechanics and Analysis of Indiana University251 and in other journals; they were then transformed into a book [269*]. According to its preface, his main intent was “to provide a detailed geometrical background for physical application of the theory”. As he was very optimistic with regard to its relation to physics, he went on: “It so happens that the detailed investigation of Einstein’s geometrical postulates opens an easy way to a physical interpretation”([269*], p. X). We have noticed in Section 9.7 that this possibly could not have been the case. In the preface of his book, Hlavatý became more explicit; his program was to encompass: (1) an investigation of the structure of the curvature and torsion imposed on space-time by the field equations, equations which he claimed to be “of a purely geometrical nature” without physical interpretation being “involved in them a priori”. The two further points of his program, i.e., (2) an attempt to identify the gravitational field and the electromagnetic field by means of the field equations, and (3) an investigation of the physical consequences of his theory, were treated only in “an outline of the basic ideas” ([269*], p. XVIII). In comparison with Einstein, Schrödinger and Tonnelat who followed their physical and mathematical intuition, Hlavatý’s investigations were much more systematical and directed first to what could be proven by mathematics; whether a relation to physics could be established became secondary to him. Although mostly working and publishing alone, he corresponded with about 40 scientists working on UFT. He also was a frequent reviewer for Mathematical Reviews (cf. Section 18.1). Hlavatý began by introducing a systematical classification of the non-symmetric metric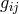 according
to the non-vanishing eigenvalues of its skew-symmetric part
according
to the non-vanishing eigenvalues of its skew-symmetric part 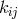 (remember
(remember 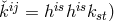 . He
distinguished three classes:
. He
distinguished three classes:
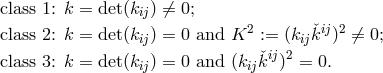
Throughout his research, the symmetric part 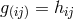 is used for raising and lowering indices. From
Eq. (30*) he concluded that there are metrics
is used for raising and lowering indices. From
Eq. (30*) he concluded that there are metrics  for which this “metric compatibility” equation
does not admit any solution”, and cases in which (30*) admits more than one solution [261*].
According to him, the condition for uniqueness of the solution is
for which this “metric compatibility” equation
does not admit any solution”, and cases in which (30*) admits more than one solution [261*].
According to him, the condition for uniqueness of the solution is 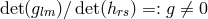 if
if
 (class 1), and
(class 1), and 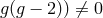 if
if 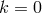 (class 2, 3). The
gravitational potential is identified with
(class 2, 3). The
gravitational potential is identified with 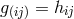 while the electromagnetic field is taken to
be252
[261*]:
while the electromagnetic field is taken to
be252
[261*]:
![κ = − sgn [ 𝜖ijrskijkrs ]](article2362x.gif) . The above classification of
. The above classification of 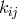 is thus valid also for the electromagnetic
field. For classes 2 and 3, Hlavatý’s definition of the electromagnetic field is a variant of one we have
already met in Section 9.7.
is thus valid also for the electromagnetic
field. For classes 2 and 3, Hlavatý’s definition of the electromagnetic field is a variant of one we have
already met in Section 9.7.
His approach was more direct than Tonnelat’s: mostly, he worked just with 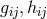 and the
decomposition (363*) met before:
and the
decomposition (363*) met before:

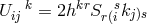 . The removal of the connection from (30*) first gave torsion as a
functional of the symmetric and skew symmetric parts of the metric via the linear equation:
with
. The removal of the connection from (30*) first gave torsion as a
functional of the symmetric and skew symmetric parts of the metric via the linear equation:
with 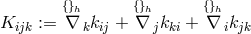 , and
, and 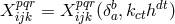 ([264*], p. 320). After torsion is
inserted into the decomposition of
([264*], p. 320). After torsion is
inserted into the decomposition of 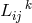 given before, the connection is known as a functional of
given before, the connection is known as a functional of 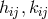 and its first derivatives. Thus, after about 80 pages in his book including degenerate cases, in the end
Mme. Tonnelat’s calculations were only simplified a bit by Hlavatý and made more transparent, with some
details added.
and its first derivatives. Thus, after about 80 pages in his book including degenerate cases, in the end
Mme. Tonnelat’s calculations were only simplified a bit by Hlavatý and made more transparent, with some
details added.
Hlavatý used the Ricci-tensors 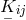 and
and 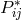 (cf. (75*) of Section 2.3.2), and proved that:
(cf. (75*) of Section 2.3.2), and proved that:

He stressed that Einstein’s weak field equations for UFT were of a purely geometrical nature with no physical interpretation needed. Equation (30*) was written in the form [261]:
where the covariant derivative is defined by (16*) in Section 2.1.1. The conditions on curvature are subsumed in with arbitrary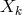 . For vanishing
. For vanishing 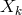 , the strong field equations, for
, the strong field equations, for  , the weak field equations
are following.
, the weak field equations
are following.
According to Hlavatý, the first two classes cannot be handled simultaneously with the third class
([266*], p. 421). This makes it more involved to read his papers, because the results proven by him must now
be distinguished according to the special class of 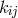 .
.
i) Fields of third class.
In the course of his investigations when he tried to interpret geometrical quantities in terms of physical
variables, Hlavatý replaced the four equations ![R {[ik],j} = 0](article2381x.gif) following from (449*) by four complicated
looking equations:
following from (449*) by four complicated
looking equations:
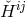 and
and 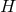 are the Ricci tensor and curvature scalar calculated from the symmetric part of the
metric
are the Ricci tensor and curvature scalar calculated from the symmetric part of the
metric 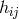 (i.e., from the Levi-Civita connection).
(i.e., from the Levi-Civita connection). 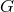 is a scalar function for which, for the 2nd class
is a scalar function for which, for the 2nd class
 , and for the third class
, and for the third class 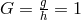 hold.
hold.
The tensor 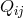 received its meaning from what Hlavatý called “the gravitational field
equations”, i.e., Einstein’s equations with a geometrical energy-momentum tensor of matter:
received its meaning from what Hlavatý called “the gravitational field
equations”, i.e., Einstein’s equations with a geometrical energy-momentum tensor of matter:
 .
.  describes both the charge density and the mass density of matter which
thus are related. As charge density it is defined by:
describes both the charge density and the mass density of matter which
thus are related. As charge density it is defined by: 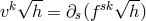 , with
, with 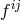 from (446*); mass
density by
from (446*); mass
density by 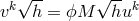 with a scalar function
with a scalar function 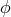 and the unit vector
and the unit vector 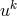 ;
; 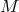 is the mass of
a particle ([269*], p. 175–176). In Hlavatý’s theory, Maxwell’s equations were taken to be:
Charge conservation was expressed by
is the mass of
a particle ([269*], p. 175–176). In Hlavatý’s theory, Maxwell’s equations were taken to be:
Charge conservation was expressed by 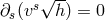 . As the first equation of (452*) is equivalent to (449*)
plus
. As the first equation of (452*) is equivalent to (449*)
plus 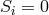 , we also have
, we also have 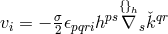 . Of course, the electromagnetic field in (446*), for the
third class, reduces to
. Of course, the electromagnetic field in (446*), for the
third class, reduces to 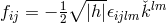 .
.
For incoherent matter, 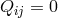 , and from (451*)
, and from (451*)  . A somewhat disappointing
consequence is that, in a manageable approximation, charged particles remain unaffected by the
electromagnetic field: they move along geodesics in the gravitational field
. A somewhat disappointing
consequence is that, in a manageable approximation, charged particles remain unaffected by the
electromagnetic field: they move along geodesics in the gravitational field 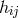 ([264], p. 329; [269*], p. 174,
187). Upon neglect of the cubic terms in
([264], p. 329; [269*], p. 174,
187). Upon neglect of the cubic terms in 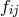 , i.e., for
, i.e., for 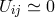 , the equation of motion coincides with the
geodesic equation:
, the equation of motion coincides with the
geodesic equation:
This is the more strange as Hlavatý claimed:
“In the unified theory the electromagnetic field is always present; hence we might look upon it as a primary field which […] creates the gravitational field. However, there is at least one known electromagnetic field which does not create a gravitational field (i.e., the field of the plane wave in the electromagnetic theory of light).” ([266*], p. 420.)
ii) Fields of class 1 and 2.
Here, 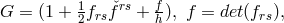 and two new quantities were introduced:
and two new quantities were introduced:
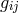 now reads as
now reads as 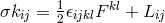 . Tangent
vectors
. Tangent
vectors 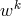 and
and 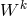 were defined by
related by
were defined by
related by 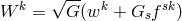 with
with 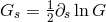 . The gravitational and Maxwell equations (451*)
and (452*) remain the same except for an exchange of
. The gravitational and Maxwell equations (451*)
and (452*) remain the same except for an exchange of 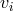 by
by  and a different complicated
expression for
and a different complicated
expression for 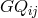 if
if ![R {[ik],j} = 0](article2422x.gif) is kept as a field equation; cf. [269*], p. 204, Eq. (20.3a,b),
p. 203 Eqs. (20.1), (20.2b). Hlavatý did present an exact spherically symmetric solution with
is kept as a field equation; cf. [269*], p. 204, Eq. (20.3a,b),
p. 203 Eqs. (20.1), (20.2b). Hlavatý did present an exact spherically symmetric solution with
 ,
, 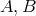 constants which is obtained from Papapetrou’s
solution (cf. Section 8.3) by setting there
constants which is obtained from Papapetrou’s
solution (cf. Section 8.3) by setting there 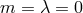 . The electromagnetic field in Hlavatý’s solution is
. The electromagnetic field in Hlavatý’s solution is
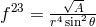 . The gravitational function replacing the gravitational constant is
. The gravitational function replacing the gravitational constant is 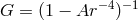 .
But in this case, according to Hlavatý “we are unable to derive the second set of Maxwell’s
equations from our field equations” ([269*], p. 208). Therefore, as for classes 1, 2, this field equation
again is replaced by (450*). In consequence, for the motion of a particle Hlavatý obtained an
improved result: A (massive) charged particle moving freely in the unified field
.
But in this case, according to Hlavatý “we are unable to derive the second set of Maxwell’s
equations from our field equations” ([269*], p. 208). Therefore, as for classes 1, 2, this field equation
again is replaced by (450*). In consequence, for the motion of a particle Hlavatý obtained an
improved result: A (massive) charged particle moving freely in the unified field 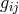 describes an
auto-parallel of the unified connection
describes an
auto-parallel of the unified connection 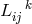 ([269], p. 211). Thus, two of the three effects in
the planetary system were the same as in general relativity; the third (Perihelion shift) in his
theory depended on the electrical field of the sun. Hlavatý did not get as far as to clearly
show the experimental physicist how this electric field enters the formula for the perihelion
shift.
([269], p. 211). Thus, two of the three effects in
the planetary system were the same as in general relativity; the third (Perihelion shift) in his
theory depended on the electrical field of the sun. Hlavatý did not get as far as to clearly
show the experimental physicist how this electric field enters the formula for the perihelion
shift.
For paths of photons Eq. (453*) still holds. If gravitation is neglected, i.e., 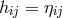 , Hlavatý found
a discrepancy with the special relativistic explanation of the Michelson-Morley experiment.
Although he referred to the judgment of Shankland et al. that Miller’s result is erroneous [575], he
concluded: “From the point of view of the unified field theory Miller’s result, properly interpreted,
is not necessarily at variance with the assumption of the constant velocity of light.” ([266],
p. 471).
, Hlavatý found
a discrepancy with the special relativistic explanation of the Michelson-Morley experiment.
Although he referred to the judgment of Shankland et al. that Miller’s result is erroneous [575], he
concluded: “From the point of view of the unified field theory Miller’s result, properly interpreted,
is not necessarily at variance with the assumption of the constant velocity of light.” ([266],
p. 471).
Hlavatý’s research will be appealing to some by its logical guideline concerning mathematical
structures. His many special cases and set up “agreements” in proving results are somewhat
bemusing for a physicist. An example is given by his publications dealing with the special case
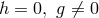 when the symmetric part
when the symmetric part 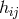 of the metric
of the metric 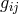 is degenerated [267, 268]. It is a
purely mathematical exercise meant to fill a gap, but is without physical meaning. For the
cases in which the theory could be applied to physical systems, in principle, Hlavatý was also
forced to alter the original field equations in order to avoid objections against the unphysical
results following from them. It is not unfair to conclude that he did not succeed in making a
break-through in the sense of his physical interpretations being more convincing than those suggested by
others.
is degenerated [267, 268]. It is a
purely mathematical exercise meant to fill a gap, but is without physical meaning. For the
cases in which the theory could be applied to physical systems, in principle, Hlavatý was also
forced to alter the original field equations in order to avoid objections against the unphysical
results following from them. It is not unfair to conclude that he did not succeed in making a
break-through in the sense of his physical interpretations being more convincing than those suggested by
others.
The investigations of his doctoral student R. Wrede were directed to the mathematical structure of the theory: He partially extended
Hlavatý’s theory to an n-dimensional space by adhering to the two principles: A.) The algebraic structure
of the theory is imposed on the space by a general real tensor 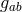 ; B.) The differential geometrical
structure is imposed on the space by the tensor
; B.) The differential geometrical
structure is imposed on the space by the tensor 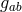 by means of a connection defined by (30*). Hlavatý’s
third principle, i.e., the existence of the constraints
by means of a connection defined by (30*). Hlavatý’s
third principle, i.e., the existence of the constraints ![r r Rab = ∂[aXb],Sar = L[ar] = 0](article2436x.gif) with an arbitrary vector
field
with an arbitrary vector
field 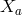 is left out [708]. The paper solves (30*) in
is left out [708]. The paper solves (30*) in 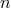 dimensions for the various possible
cases.
dimensions for the various possible
cases.
12.3 Other contributions
A theoretician of the younger generation and assistant at Princeton University, R. L. Arnowitt , tried to look at UFT from the point of view of the electromagnetic field forming a link between the description of microscopic charges by quantum field theory and macroscopic ray optics [5*]. He introduced four postulates:
- Any unified field theory should reduce to Einstein–Maxwell theory in a first approximation for weak electromagnetic fields.
- First-order corrections to the Coulomb field of the electron should not become appreciable for
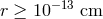 .
.
- The affine connection has the form
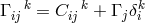 , where
, where 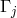 is related to the vector
potential of the Maxwell field. Also
is related to the vector
potential of the Maxwell field. Also 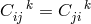 is assumed.
is assumed.
- The Lagrangian must be invariant under the combined gauge
transformation
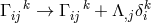 and (for the metric)
and (for the metric) ![gij → exp[2Λ(x )] gij](article2444x.gif) . The metric
tensor is also symmetric.
. The metric
tensor is also symmetric.
The appearance of a microscopic length-parameter (and the cosmological constant) in his Lagrangian
and the occurrence of two “metrical” tensors turned out to be a consequence of the postulates. The
symmetrical first one 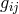 is supposed to “be measured by rods and clocks” and used to set up the
Lagrangian; the second asymmetric one is derived from the Lagrangian:
is supposed to “be measured by rods and clocks” and used to set up the
Lagrangian; the second asymmetric one is derived from the Lagrangian: 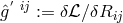 . It is an
auxiliary device for the introduction of the electromagnetic field. Arnowitt chose the Lagrangian:
. It is an
auxiliary device for the introduction of the electromagnetic field. Arnowitt chose the Lagrangian:
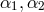 of dimension
of dimension 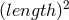 . The theory looks similar to Buchdahl’s
gauge-invariant UFT published in the same year (cf. Section 13.1) but is different. Immediately,
. The theory looks similar to Buchdahl’s
gauge-invariant UFT published in the same year (cf. Section 13.1) but is different. Immediately,
In order to obtain the field equations, the quantities 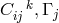 and
and 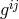 are to be varied. From the first
two variations
are to be varied. From the first
two variations ![′[is] ′ij ˆg ;s = 0, ˆg ;k = 0](article2453x.gif) and
and 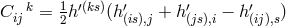 resulted where
resulted where 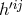 was
introduced by
was
introduced by 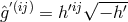 and interpreted to be the “gravitational” metric tensor. The first of these
equations was rewritten as sourceless Maxwell equation such that
and interpreted to be the “gravitational” metric tensor. The first of these
equations was rewritten as sourceless Maxwell equation such that 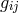 is the “electromagnetic” metric
tensor:
is the “electromagnetic” metric
tensor:
![fij = − a− 12R [ij]](article2459x.gif) , and the constant a is determined later in a weak field approximation to be
, and the constant a is determined later in a weak field approximation to be
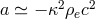 with
with 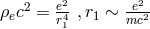 the classical electron radius,
the classical electron radius,  the electron mass, and
the electron mass, and  the
gravitational constant in Einstein’s equations.
the
gravitational constant in Einstein’s equations.
After some manipulation, variation with respect to  led to:
led to:
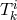 was interpreted as ‘the electromagnetic stress-energy tensor”. After linearization, (459*) formally
became Einstein’s equations. Again, in a weak field approximation introduced by
was interpreted as ‘the electromagnetic stress-energy tensor”. After linearization, (459*) formally
became Einstein’s equations. Again, in a weak field approximation introduced by 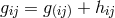 with
small
with
small 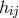 , the free parameters
, the free parameters 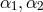 were fixed to be
were fixed to be 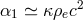 and
and 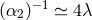 with the cosmological constant
with the cosmological constant 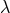 . Thus,
. Thus, 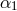 is the microscopic length parameter mentioned
above. In linear approximation, the author also has obtained a static, spherically symmetric
Schwarzschild-like solution with an event horizon and finite electrical field (and field energy) for
is the microscopic length parameter mentioned
above. In linear approximation, the author also has obtained a static, spherically symmetric
Schwarzschild-like solution with an event horizon and finite electrical field (and field energy) for
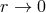 .
.
A further contribution came from B. Kursunŏglu, whom we have met before in Section 9.3.3, now situated in Coral Gables, Florida. He continued to alter and study his variant of the Einstein–Schrödinger field equations [345]. In place of (300*) – (302*), he postulated the system:253
where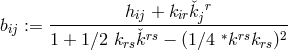
with
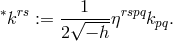
The denominator is related to 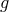 .
.
The auxiliary field 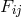 satisfies the vacuum Maxwell equations.
satisfies the vacuum Maxwell equations.

![L ijk = Δ ijk + aijk, (432 ) 1 Δ ijk= -g(kl) [gli,j + gjl,i − gji,l], (433 ) 2](article2318x.gif)
![2 aijk = 2g[lk]Δ [ijl] − -Δ [ij]k. (434 ) 3](article2322x.gif)

![k k k 1-(kl) (kl) s Sij = Δ [ij] + a[ij] = 3g Δ [ij]l + 2g g[sl]Δ [ij] . (436 )](article2324x.gif)


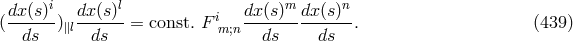



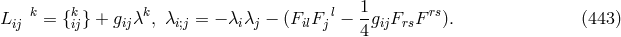
![g S r + g S r= 0. (444 ) [ir] jk [jr] ik](article2342x.gif)
![L k = {k }h, L k= S k= 1mkr (krj,i + kir,j + kji,r). (445 ) (ij) ij [ij] ij 2](article2343x.gif)
![1 ∘ --- 1∘ --- fij := √--[κ |k |kij − -- |h|𝜖ijrsˇkrs] g 2 ij -1-- ∘ --ˇij 1∘ --- ijrs f := √g--[κ |k |k − 2 |h|𝜖 krs] (446 )](article2361x.gif)


![K ij = ∂ [iXk] (449 ) −](article2376x.gif)
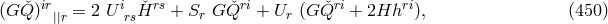


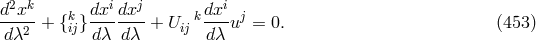
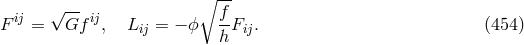
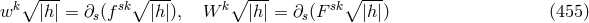
![∫ ∫ L = d4xℒ (x) = d4x √ − g-[α R R gijgrs + α (grsR )2] (456 ) 1 ir js 2 rs](article2447x.gif)
![√ --- ˆg′(ij) = − g [α1R (rs)girgjs + α2 gijgrsR(rs)],ˆg′[ij] = α1R [sr]girgjs. (457 )](article2450x.gif)
![√ --- ir qs [ − gg g frs],q = 0 (458 )](article2458x.gif)
![ip rs 1-i qp rs ip rs 1- i rs 2 i α1 [g R(kr)g R (ps) − 4δkg R (qr)g R (ps)] + α2 [g R (kp)g R(rs) − 4δk(g R (rs))] = α1aT k (459 )](article2465x.gif)
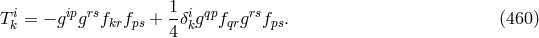
![[il] ˆg ,l = 0, (461 ) K + p2(h − b ) = 0, (462 ) − (ik) ij ij K [ik] + p2(qkik − Fik) = 0, (463 ) −](article2478x.gif)