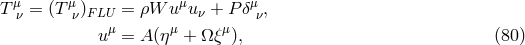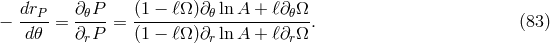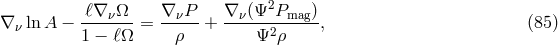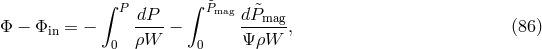4 Thick Disks, Polish Doughnuts, & Magnetized Tori

In this section we discuss the simplest analytic model of a black hole accretion disk – the “Polish doughnut.” It is simplest in the sense that it only considers gravity (Section 2), plus a perfect fluid (Section 3.1.1), i.e., the absolute minimal description of accretion. We include magnetized tori in Section 4.2, which allows for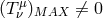 , but otherwise 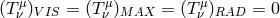throughout this section.

4.1 Polish doughnuts

Paczyński and his collaborators developed, in the late 1970s and early 1980s, a very general method of constructing perfect fluid equilibria of matter orbiting around a Kerr black hole [139, 236, 235, 234]. They assumed for the stress energy tensor and four velocity,

and derived from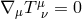 that, In the case of a barytropic fluid , the right-hand side of Eq. (81) is the gradient of a scalar function, and thus the left-hand side must also be the gradient of a scalar, which is possible if and only if This statement is one of several useful integrability conditions, collectively called von Zeipel theorems, found by a number of authors [51, 29, 1, 156].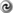

In real flows, the function 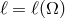is determined by dissipative processes that have timescales much longer than the dynamical timescale, and are not yet fully understood. Paczyński realized that instead of deriving 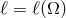from unsure assumptions about viscosity that involve a free function fixed ad hoc (e.g., by assuming 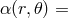const), one may instead assume the result, i.e., assume 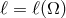. Assuming 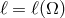is not self-consistent, but neither is assuming 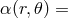const.

In Boyer–Lindquist coordinates, the equation for the equipressure surfaces, 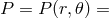const, may be written as 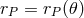, with the function 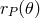given by

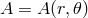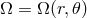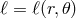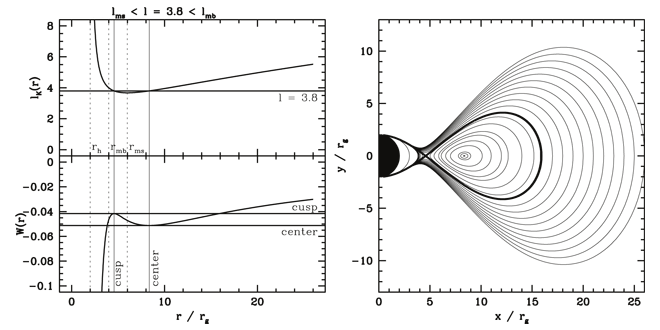
Using the expressions for , , and from Section 2 (Eqs. 21 and 22), one can integrate Eq. (83) to get the equipressure surfaces. A description of how to do this for both Schwarzschild and Kerr black holes is given in [57]. Figure 4 illustrates the simplest (and important) case of .

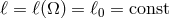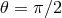Figure 4: In equilibrium, the equipressure surfaces should coincide with the surfaces shown by the solid lines in the right panel. Note the Roche lobe, self-crossing at the cusp. The cusp and the center, both located at the equatorial plane , are circles on which the pressure gradient vanishes. Thus, the (constant) angular momentum of matter equals the Keplerian angular momentum at these two circles, 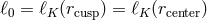, as shown in the upper left panel. In this figure 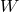refers to the effective potential. Image reproduced by permission from [98], copyright by RAS.

Another useful way to think about thick disks is from the relativistic analog of the Newtonian effective potential ,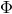

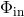where is the potential at the boundary of the thick disk. For constant angular momentum 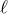, the form of the potential reduces to 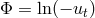. Provided 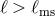, the potential 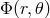will have a saddle poin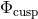t at 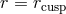, 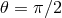. We can define the parameter 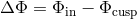as the potential barrier (energy gap) at the inner edge of the disk. If , the disk lies entirely within its Roche lobe, whereas if 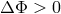, matter will spill into the black hole even without any loss of angular momentum.

Before leaving the topic of Polish doughnuts, we should point out that, starting with the work of Hawley, Smarr, and Wilson [125], this simple, analytic solution has been the most commonly used starting condition for numerical studies of black hole accretion.

4.2 Magnetized Tori

Komissarov [156] was able to extend the Polish doughnut solution by adding a purely azimuthal magnetic field to create a magnetized torus. This is possible because a magnetic field of this form only enters the equilibrium solution as an additional pressure-like term. For example, the extended form of Eq. (81) is

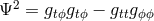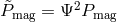where and Eq. (84) becomes where . Komissarov [156] gives a procedure for solving the case of a barotropic magnetized torus with constant angular momentum (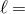 const.).