4 The Hole Argument and Some Extensions 38
After defining geometric and algebraic structures, a space is defined as a set of points with a geometric structure that is invariant under some group of transfomations of its points. Then I discuss product and quotient spaces, fibered spaces, and theories based on these spaces, in particular permutable and generally permutable theories (Section 4.1).Up to this point, the only structures discussed have been relations between the elements of a set. But all definitions are still applicable – appropriately modified, of course – when additional structures are introduced. In particular, the case of most physical interest is that of geometric object fields defined on a differentiable manifold (Section 4.2). They provide the framework for coordinate-independent definitions of covariant and generally covariant theories, followed by a precise formulation of the of the original hole argument against general covariance and of the way to avoid its conclusion, discussed informally in Section 2.
Then I discuss fiber bundles, which consist of a total space, a base space, and a projection operator. Under certain circumstances, the base space may be defined as the quotient of the total space divided by an equivalence relation defining its fibers (Section 4.3) This approach allows a more precise formulation of Einstein’s vision of general relativity, discussed informally in Section 3.2.
Finally, the distinction between natural and gauge natural bundles is discussed, and between the concepts of covariance and general covariance when applied to theories defined on each type of bundle (Section 4.4).
A number of philosophical concepts used but not defined in this section, such as: intrinsic and extrinsic properties, internal and external relations, and quiddity and haecceity, are discussed in the Appendix B.
4.1 Structures, algebraic and geometric, permutability and general permutability
Consider a set 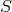 of elements
of elements 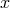 ,
, 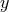 ,
,  , etc., together with a set of relations
, etc., together with a set of relations 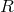 between its
elements.39
There is a major distinction between a geometry and an algebra:
between its
elements.39
There is a major distinction between a geometry and an algebra:
Geometry:
In a geometry, the elements of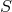 (hereafter called points and symbolized by
(hereafter called points and symbolized by 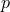 ,
, 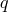 ,
etc.)40
all are of the same quiddity (i.e., of the same nature) but lack haecceity (i.e., are not inherently individuated):
The only distinctions between the points arise from a set of internal relations
,
etc.)40
all are of the same quiddity (i.e., of the same nature) but lack haecceity (i.e., are not inherently individuated):
The only distinctions between the points arise from a set of internal relations 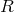 between them. If we abstract
from these relations, the set
between them. If we abstract
from these relations, the set 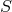 is invariant under
is invariant under 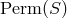 , the group of all permutations of the points of
, the group of all permutations of the points of
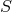 .41
The set of relations defining a geometry structure or geometry
.41
The set of relations defining a geometry structure or geometry 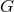 on
on 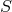 will be symbolized by
will be symbolized by 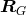 . The
maximal subgroup
. The
maximal subgroup 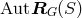 of
of 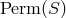 that preserves all these relations between the points of
that preserves all these relations between the points of 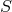 is
called the symmetry or automorphism group of this geometry, and could just as well be used to define
it.42
is
called the symmetry or automorphism group of this geometry, and could just as well be used to define
it.42
Obviously, 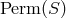 is the maximal possible automorphism group; so a study of its subgroups and
their relation to each other is equivalent to a study of all possible geometries on
is the maximal possible automorphism group; so a study of its subgroups and
their relation to each other is equivalent to a study of all possible geometries on 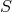 and their relation to
each other.
and their relation to
each other.
Algebra:
In contrast to a geometry, in an algebra each element (symbolized by ,
, 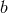 , etc.) in
addition to having the same quiddity also has an intrinsic haecceity (individuality). An algebraic
structure or algebra
, etc.) in
addition to having the same quiddity also has an intrinsic haecceity (individuality). An algebraic
structure or algebra 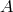 on a set is also defined by a set of relations
on a set is also defined by a set of relations 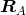 between its
elements; but these are external relations, which do not affect the intrinsic individuality of each
element.43
between its
elements; but these are external relations, which do not affect the intrinsic individuality of each
element.43
Coordinatization:
Since Descartes introduced analytic geometry, it has proved convenient and often necessary to apply algebraic methods in the solution of geometrical problems. This is done by a coordinatization of the geometry (see Weyl, 1946, for this term): A one-one correspondence is set up between the points of the geometry and certain elements of an appropriately chosen algebra. This coordinatization assigns to each point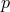 of the geometry an element a of the algebra, called its coordinate
and symbolized by
of the geometry an element a of the algebra, called its coordinate
and symbolized by 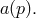 Now certain algebraic operations can be given a geometrical interpretation, and
vice versa. But, by individuating the points of a geometry, a coordinatization negates their homogeneity,
turning the geometry into an algebra. The only way to restore their homogeneity is to negate
the coordinatization as follows: Introduce the class of all admissible coordinatizations of the
geometry44
based on the given algebra, so that each point of the geometry will have every admissible element of
the algebra as its coordinate in at least one admissible coordinate system. Transformations
between two admissible coordinate systems are called admissible coordinate transformations; they
usually form a group that includes a subgroup isomorphic to the automorphism group of the
geometry.
Now certain algebraic operations can be given a geometrical interpretation, and
vice versa. But, by individuating the points of a geometry, a coordinatization negates their homogeneity,
turning the geometry into an algebra. The only way to restore their homogeneity is to negate
the coordinatization as follows: Introduce the class of all admissible coordinatizations of the
geometry44
based on the given algebra, so that each point of the geometry will have every admissible element of
the algebra as its coordinate in at least one admissible coordinate system. Transformations
between two admissible coordinate systems are called admissible coordinate transformations; they
usually form a group that includes a subgroup isomorphic to the automorphism group of the
geometry.
Permutations and the basic identity.
There are two distinct ways in which the assignment of all admissible coordinates to each point of a geometry may be accomplished.- Active point transformations: Keep the coordinate system fixed,
 , and permute the
points of the geometry:
, and permute the
points of the geometry: 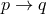 ,
, 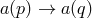 .
.
- Passive coordinate transformations: Keep the points of the geometry fixed,
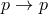 , and
carry out an admissible coordinate transformation of the elements of the algebra:
, and
carry out an admissible coordinate transformation of the elements of the algebra: 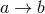 ,
,
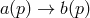 .
.
The terms “active” and “passive” refer to the effects of a transformation on the points of the geometry. A passive coordinate transformation is an active transformation of the elements of the algebra.45
Two active permutation groups of any geometry have already been introduced:
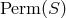 , the group of all permutations of the elements of
, the group of all permutations of the elements of 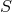 ;
;
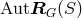 , the subgroup of
, the subgroup of 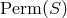 consisting of the permutations that belong to the
automorphism group
consisting of the permutations that belong to the
automorphism group 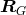 of a particular geometry
of a particular geometry 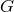 .
.
Relations may also be permuted. Let 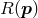 symbolize a relation between the set
symbolize a relation between the set 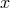 of all points of
of all points of
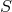 .46
.46
Consider a permutation 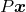 of the elements of
of the elements of 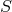 . Define the permuted relation
. Define the permuted relation 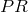 as follows:
as follows: 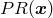 holds iff
holds iff 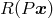 does. When a permutation
does. When a permutation 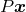 is carried out,
the relation
is carried out,
the relation 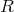 will be said to be “carried along” if it is also permuted into the relation
will be said to be “carried along” if it is also permuted into the relation
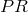 .47
.47
It follows that, if 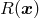 is valid, then so is
is valid, then so is 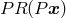 .
.
The basic identity for the group of all permutations 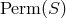 .
.
By virtue of the intrinsic homogeneity of its
points, a geometry 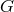 remains unchanged if, for each Permutation
remains unchanged if, for each Permutation 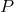 of
of  , the corresponding
permutation
, the corresponding
permutation  of the set of relations
of the set of relations 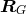 defining
defining 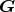 is also carried out. For any relation
is also carried out. For any relation
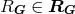 , it is clear that
, it is clear that 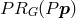 holds if and only if
holds if and only if 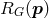 holds, so
holds, so 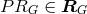 ;
thus
;
thus 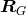 and
and 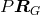 describe the same geometry. I shall refer to this result as the basic or
trivial identity for the group
describe the same geometry. I shall refer to this result as the basic or
trivial identity for the group 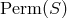 : it holds for any geometry based on a subgroup of
: it holds for any geometry based on a subgroup of
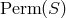 .
.
Equivalence relations and quotient maps.48
An equivalence relation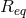 on any set
on any set 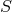 is a two-place relation having the following three properties:
For all
is a two-place relation having the following three properties:
For all 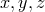 in
in  , it is reflexive:
, it is reflexive:  holds; symmetric: if
holds; symmetric: if  holds, then so does
holds, then so does
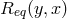 ; and transitive: if
; and transitive: if 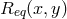 and
and 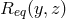 both hold, then so does
both hold, then so does 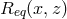 . If the context
is clear, one often abbreviates
. If the context
is clear, one often abbreviates 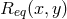 by
by 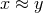 . An equivalence relation divides
. An equivalence relation divides 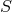 into
equivalence classes
into
equivalence classes 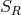 , often also called its orbits (see Neumann et al., 1994
, often also called its orbits (see Neumann et al., 1994 , Chapter V).
Every element of
, Chapter V).
Every element of 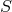 belongs to one and only one such equivalence class. The quotient set of
belongs to one and only one such equivalence class. The quotient set of
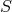 by
by 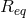 , often called the orbit space and abbreviated
, often called the orbit space and abbreviated 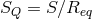 , is defined by the
condition that each element of the quotient set corresponds to one and only one such equivalence
class.
, is defined by the
condition that each element of the quotient set corresponds to one and only one such equivalence
class.
Product sets and quotient sets.
Given two sets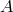 and
and 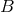 , we can form the product set
, we can form the product set 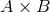 ,
consisting of all pairs of elements
,
consisting of all pairs of elements 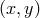 , with
, with 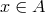 and
and 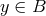 .
. 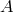 mapping
mapping 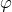 from the domain A
to the range or codomain
from the domain A
to the range or codomain 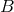 (see Lawvere and Schanuel, 1997, pp. 13–14), often symbolized
(see Lawvere and Schanuel, 1997, pp. 13–14), often symbolized 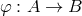 ,
is defined as a subset of
,
is defined as a subset of 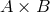 , such that for each
, such that for each 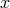 in the domain there is one and only one
in the domain there is one and only one 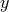 in its
range.
in its
range.
In various contexts, “mappings” might also be called functions, transformations,
or operators. Homomorphisms, isomorphisms, homeomorphisms, diffeomorphisms,
continuous or differentiable maps will be more attached to certain classes of mappings,
which “preserve” certain structures on the sets which are their domains and ranges
(Hermann, 1973 , p. 3).
, p. 3).
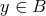 , there is at least-one element
, there is at least-one element 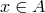 that maps
onto
that maps
onto 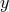 . If both mappings
. If both mappings 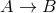 and
and 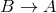 are surjective, the mapping is called bijective. If the
bijective map preserves all structures on
are surjective, the mapping is called bijective. If the
bijective map preserves all structures on 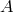 and
and 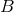 ,
, 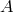 and
and 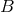 are said to be isomorphic. If the
mapping
are said to be isomorphic. If the
mapping 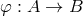 is surjective, the set
is surjective, the set 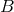 is isomorphic to the quotient set
is isomorphic to the quotient set 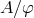 ; so
; so 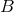 can
actually be defined as the quotient set.
can
actually be defined as the quotient set.
This “passing to the quotient” is a way of defining new spaces and mappings that is very important in all of mathematics, particularly in algebra and differential geometry. (Hermann, 1973, p. 5).
This possibility allows us to realize Einstein’s vision of general relativity (see Section 3.2), which in this
context is simply: If no 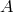 , then no
, then no 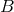 . We can define the mapping or morphism
. We can define the mapping or morphism 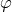 from
from 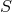 to
to 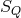 ,
,
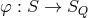 , which projects each element
, which projects each element 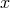 of
of 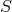 into the element
into the element 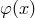 of
of 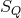 corresponding to
the equivalence class that includes
corresponding to
the equivalence class that includes 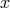 . Conversely a section of
. Conversely a section of 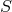 is an inverse mapping
is an inverse mapping 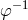 from the
point
from the
point 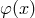 of
of 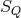 to a unique point
to a unique point 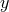 in the equivalence class of
in the equivalence class of 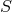 that maps into that point of
that maps into that point of
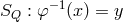 , with
, with 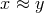 .
.
So far, these concepts can be applied to any set. If 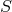 is a geometry with automorphism group
is a geometry with automorphism group 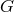 , it
is referred to as a
, it
is referred to as a 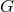 -space (see Neumann et al., 1994
-space (see Neumann et al., 1994 , pp. 74ff). The equivalence relation is said to be
, pp. 74ff). The equivalence relation is said to be
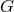 -invariant if, whenever
-invariant if, whenever 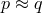 holds for two points of
holds for two points of 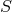 , then it follows that
, then it follows that 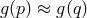 for
all
for
all 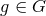 . Consequently, the action of an element
. Consequently, the action of an element 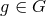 on
on 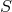 preserves the orbits of
preserves the orbits of
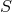 but permutes them; so all orbits, henceforth called fibers, must be isomorphic to what is
called a typical fiber. The quotient set
but permutes them; so all orbits, henceforth called fibers, must be isomorphic to what is
called a typical fiber. The quotient set 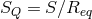 is itself a
is itself a 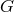 -space called the quotient
space.
-space called the quotient
space.
Fibered or fiber spaces.
A fibered space consists of a total space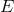 ; a base space
; a base space 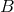 ; and a projection
operator
; and a projection
operator 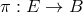 that is a surjective mapping, as defined above. The fiber
that is a surjective mapping, as defined above. The fiber 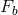 over each point
over each point
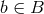 is the set of all inverse elements
is the set of all inverse elements 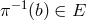 ; that is, all elements
; that is, all elements 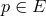 such that
such that
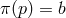 . A section
. A section 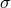 of a fiber space is a choice of one element on each fiber
of a fiber space is a choice of one element on each fiber 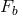 for every
for every
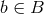 .
To convert a homogeneous set
.
To convert a homogeneous set 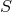 with an equivalence relation
with an equivalence relation 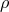 into a fibered space, let
into a fibered space, let 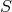 constitute the total space
constitute the total space 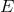 ; then
; then 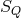 forms the base space
forms the base space 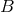 , and the mapping
, and the mapping 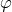 becomes the projection operator
becomes the projection operator 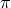 . If
. If 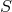 is a geometry with automorphism group
is a geometry with automorphism group 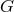 ,
then
,
then 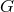 preserves the equivalence classes; so all the fibers are isomorphic, resulting in a fiber
bundle:
preserves the equivalence classes; so all the fibers are isomorphic, resulting in a fiber
bundle:
A fiber bundle 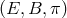 consists of: 1) a total space
consists of: 1) a total space 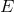 , divided into fibers by an equivalence relation
, divided into fibers by an equivalence relation
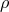 , all of these fibers being isomorphic to a typical fiber
, all of these fibers being isomorphic to a typical fiber 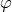 ; 2) a base space
; 2) a base space 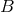 that is isomorphic to the
quotient
that is isomorphic to the
quotient 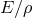 ; and 3) a projection operator
; and 3) a projection operator 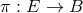 that takes each point of its domain
that takes each point of its domain 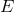 into the
point
into the
point 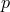 of its range
of its range 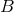 that corresponds to the fiber including
that corresponds to the fiber including 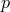 . A section of the bundle is a
mapping
. A section of the bundle is a
mapping 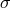 that takes each point
that takes each point 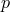 of its domain
of its domain 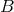 into a unique point of its range,
consisting of the set of fibers of
into a unique point of its range,
consisting of the set of fibers of 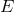 . The point of
. The point of 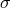 on the fiber
on the fiber 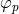 over
over 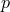 is symbolized by
is symbolized by
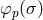 . If
. If 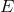 has the automorphism group
has the automorphism group 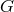 , the action of an element
, the action of an element 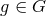 on the points
of any section
on the points
of any section  will result in a new section
will result in a new section  ; symbolically:
; symbolically: 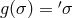 . So, given one
section
. So, given one
section 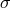 , the action of the elements of
, the action of the elements of 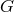 produces a whole equivalence class of sections
produces a whole equivalence class of sections
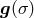 .
.
Theories, permutable and generally permutable.
A theory of a certain type is a procedure for producing models of that type. A particular theory of that type is a rule for selecting a subset of these models. One type of theory is defined by the choice of a fiber bundle with automorphism group ; its models are the
sections of this bundle. A particular theory is a rule for choosing a subset of sections of the bundle as
models. If the rule is such that, when
; its models are the
sections of this bundle. A particular theory is a rule for choosing a subset of sections of the bundle as
models. If the rule is such that, when 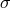 is a model, then so is the entire equivalence class of sections
is a model, then so is the entire equivalence class of sections
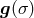 , the theory is permutable. It is generally permutable if this entire equivalence class is interpreted as a
single model of the theory. In terms of the distinction between syntax and semantics, one may
say: While each section of a theory is always syntactically distinguishable from the others, in
a permutable theory they may also be semantically distinguishable. However, in a generally
permutable theory they are not; only an entire equivalence class of sections has a unique semantic
interpretation.
Take Euclidean plane geometry, for example. All assertions about geometric figures, such as right
triangles, rectangles, circles, etc., are invariant under its automorphism group, which consists of translations
and rotations; so it is certainly a permutable theory. But these assertions actually apply to the whole
equivalence class of geometric figures satisfying any of these definitions; so it is a generally permutable
theory.
, the theory is permutable. It is generally permutable if this entire equivalence class is interpreted as a
single model of the theory. In terms of the distinction between syntax and semantics, one may
say: While each section of a theory is always syntactically distinguishable from the others, in
a permutable theory they may also be semantically distinguishable. However, in a generally
permutable theory they are not; only an entire equivalence class of sections has a unique semantic
interpretation.
Take Euclidean plane geometry, for example. All assertions about geometric figures, such as right
triangles, rectangles, circles, etc., are invariant under its automorphism group, which consists of translations
and rotations; so it is certainly a permutable theory. But these assertions actually apply to the whole
equivalence class of geometric figures satisfying any of these definitions; so it is a generally permutable
theory.
On the other hand, plane analytic geometry includes a choice of origin, unit of length, and a pair of
rectangular axes. So all of its assertions are still permutable; but some of them include references to the
origin, axes, etc. We can distinguish, for example, between a circle of radius  centered at the
origin, and one of the same radius centered at some other point. So plane analytic geometry is a
permutable theory, but not generally permutable. The reason, of course, is that the choice of
a unique preferred coordinate system converts the Euclidean plane from a geometry into an
algebra.
centered at the
origin, and one of the same radius centered at some other point. So plane analytic geometry is a
permutable theory, but not generally permutable. The reason, of course, is that the choice of
a unique preferred coordinate system converts the Euclidean plane from a geometry into an
algebra.
4.2 Differentiable manifolds and diffeomorphisms, covariance and general covariance49
For the space-time theories forming the main topic of this review, 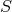 is often a four-dimensional
differentiable manifold
is often a four-dimensional
differentiable manifold 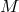 ; and the analogue of
; and the analogue of 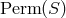 is
is 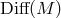 , the diffeomorphism group
consisting of all differentiable point transformations of the points
, the diffeomorphism group
consisting of all differentiable point transformations of the points  of
of 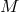 . Any given, fixed geometric
structures defined on
. Any given, fixed geometric
structures defined on 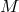 , such as a metric tensor field, will be symbolized by
, such as a metric tensor field, will be symbolized by 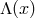 ; they represent the
analogue of the relations
; they represent the
analogue of the relations 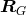 . The
. The 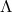 -geometry of
-geometry of 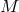 is also defined by the invariance of these
is also defined by the invariance of these 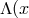 )
under the action of some Lie subgroup
)
under the action of some Lie subgroup 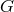 of
of 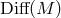 . In other words,
. In other words, 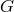 plays the role,
analogous to that of
plays the role,
analogous to that of 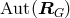 , of the automophism group
, of the automophism group 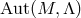 of the
of the 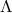 -geometry of
-geometry of
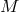 . And just as in that case, here every
. And just as in that case, here every  -space can also be defined as a quotient or orbit
space:
-space can also be defined as a quotient or orbit
space:
Every 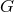 -space can be expressed as in just one way as a disjoint union of a family of
orbits. (Neumann et al., 1994, p. 51)
-space can be expressed as in just one way as a disjoint union of a family of
orbits. (Neumann et al., 1994, p. 51)
Just as in analytic geometry, one may set up ordinary and partial differential equations
for various particles and fields on 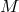 . Denote a set of such geometric object fields on
. Denote a set of such geometric object fields on 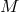 collectively by the symbol
collectively by the symbol 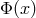 , and consider the effect of an element
, and consider the effect of an element 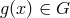 on
on
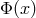 .50
From the definition of a geometric object (see Schouten, 1954, pp. 67–68) it follows that if
.50
From the definition of a geometric object (see Schouten, 1954, pp. 67–68) it follows that if 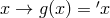 ,
then
,
then 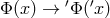 .
.
Geometric quantities form an important subclass of geometric objects which includes all tensor fields.
Their transformation law under 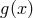 is linear and homogeneous in the components of
is linear and homogeneous in the components of 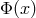 and
homogeneous in the derivatives of
and
homogeneous in the derivatives of 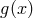 .
.
In both Galilean space-time (see Yaglom, 1979) and in special relativistic space-time (Minkowski space),
 is a ten parameter Lie group. Four of these parameters generate spatial and temporal translations of
the points, making these space-time geometries homogeneous. And in both, the six remaining
parameters act at each point of space-time: three generate spatial rotations and three generate
“boosts”, making both space-times non-isotropic. But they do so in different ways because their
“boosts” differ: For Galilean space time, they are Galilei transformations that preserve the
invariance of the absolute time. For Minkowski space-time, they are Lorentz transformations that
combine spatial and temporal intervals into an invariant, truly four-dimensional space-time
interval. Both of these groups are subgroups of
is a ten parameter Lie group. Four of these parameters generate spatial and temporal translations of
the points, making these space-time geometries homogeneous. And in both, the six remaining
parameters act at each point of space-time: three generate spatial rotations and three generate
“boosts”, making both space-times non-isotropic. But they do so in different ways because their
“boosts” differ: For Galilean space time, they are Galilei transformations that preserve the
invariance of the absolute time. For Minkowski space-time, they are Lorentz transformations that
combine spatial and temporal intervals into an invariant, truly four-dimensional space-time
interval. Both of these groups are subgroups of 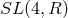 , the group of four-volume-preserving
transformations.51
And both theories have a homogeneous, flat affine connection in common that is the mathematical
expression of the Newton’s first law of inertia. Its invariance group is
, the group of four-volume-preserving
transformations.51
And both theories have a homogeneous, flat affine connection in common that is the mathematical
expression of the Newton’s first law of inertia. Its invariance group is 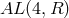 , which is a subgroup of
, which is a subgroup of
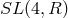 .
.
Newtonian gravitational theory, in the form which incorporates the equivalence principle, preserves the
global space-time structure of Galilean space-time, but abandons the homogeneous flatness of the
affine connection in favor of a non-flat affine connection that is the mathematical expression of
the dynamical inertia-gravitational field. This field is non-homogeneous, but its compatibility
with the space-time structure requires that locally it remain invariant under 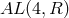 , which
means that its globally automorphism group must be
, which
means that its globally automorphism group must be 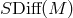 , the group of unimodular
diffeomorphisms.
, the group of unimodular
diffeomorphisms.
General relativity similarly abandons the homogeneous flatness of the affine connection in favor of a
non-flat affine connection that is the mathematical expression of the dynamical inertia-gravitational field.
But, in order to preserve its compatibility with the special-relativistic chrono-geometry expressed by the
metric tensor, the latter must also become a dynamical field. It preserves the local space-time structure of
the special theory at each point. But globally both dynamical fields must have automorphism groups
consisting of diffeomorphisms of 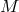 , the space-tme manifold, now itself no longer globally fixed.
Traditionally,
, the space-tme manifold, now itself no longer globally fixed.
Traditionally, 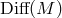 , the full diffeomorphism group, has been assumed to be the correct
automorphism group for general-relativistic theories. However, there are good arguments for
restricting this group to
, the full diffeomorphism group, has been assumed to be the correct
automorphism group for general-relativistic theories. However, there are good arguments for
restricting this group to  , the group of unimodular diffeomorphisms with determinant
one.
, the group of unimodular diffeomorphisms with determinant
one.
But first some definitions are needed (see, e.g., Wikipedia: Group action). The action of 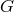 is said to
be effective if its identity element is the only one that takes each point into itself: That is, if
is said to
be effective if its identity element is the only one that takes each point into itself: That is, if
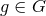 ,
, 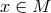 and
and 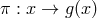 is such that
is such that 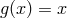 for all
for all 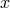 , then
, then 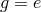 , the
identity element of
, the
identity element of 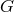 . The action is transitive if
. The action is transitive if  is a map onto
is a map onto 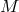 that connects any
two of its points: That is for any two points
that connects any
two of its points: That is for any two points 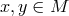 , there is always a
, there is always a 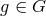 for which
for which
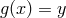 .
.
The stabilizer group 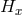 at a point
at a point 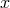 of
of 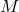 is the subgroup of transformations
of
is the subgroup of transformations
of 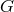 that leave the point
that leave the point  invariant: That is,
invariant: That is, 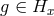 if and only if
if and only if
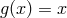 .52
Since
.52
Since 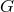 is a Lie group,
is a Lie group, 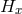 is a closed subgroup at each point of
is a closed subgroup at each point of 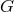 and these stabilizer groups are
conjugate subgroups of
and these stabilizer groups are
conjugate subgroups of  . Indeed,
. Indeed, 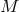 is isomorphic to
is isomorphic to 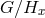 ; so one may actually define a geometry
by the pair
; so one may actually define a geometry
by the pair 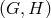 , where
, where 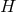 is a closed subgroup of
is a closed subgroup of 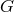 .
.
The action of 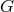 is free or semiregular if its stabilizer group is the identity: That is, if
is free or semiregular if its stabilizer group is the identity: That is, if 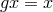 for
some point
for
some point 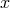 , then
, then 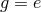 , the identity element of
, the identity element of 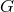 ; equivalently, if
; equivalently, if 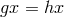 for some
for some 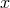 , then
, then
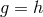 . For example, the translation groups discussed above act freely on Galilean and special relativistic
space-times.
. For example, the translation groups discussed above act freely on Galilean and special relativistic
space-times.
Now we are ready to return to the question of automorphism groups for general relativistic theories. The
action of the stabilizer of 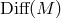 on the tangent space at each point
on the tangent space at each point  of
of 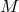 is
is 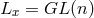 , the
group of all linear transformations at
, the
group of all linear transformations at 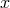 . But consider the objects defining the geometry of a
general-relativistic space-time with
. But consider the objects defining the geometry of a
general-relativistic space-time with 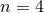 : Again, if one wants to preserve the four-volumes of space-time,
which are needed to formulate meaningful physical averages, one must restrict these transformations to
: Again, if one wants to preserve the four-volumes of space-time,
which are needed to formulate meaningful physical averages, one must restrict these transformations to
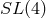 , the group of 23 special linear transformations with unit determinant. The linear affine connection
at
, the group of 23 special linear transformations with unit determinant. The linear affine connection
at 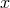 , which represents the inertio-gravitational field, is only invariant under the subgroup
, which represents the inertio-gravitational field, is only invariant under the subgroup
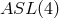 , the group of affine transformations with unit determinant. And the invariance group
of the metric tensor, which represents the chrono-geometry, is even further restricted to the
pseudo-orthogonal subgroup
, the group of affine transformations with unit determinant. And the invariance group
of the metric tensor, which represents the chrono-geometry, is even further restricted to the
pseudo-orthogonal subgroup 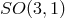 of
of 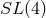 . In short, globally physical considerations
suggest the need to start from
. In short, globally physical considerations
suggest the need to start from 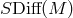 as the automorphism group of general-relativistic
theories.
as the automorphism group of general-relativistic
theories.
So physically, 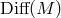 overshoots the mark by allowing non-unimodular transformations, i.e,
transformations with any value of their determinant at a point. Geometrically, they correspond to similarity
transformations, which preserve the shape but not the size of four-volumes in space-time. Usually, one
“compensates” for this unwanted change of size by introducing tensor densities: When appropriate weights
are introduced for various tensors, these densities can undo the effects of the size changes produced by
non-unimodular transformations.
overshoots the mark by allowing non-unimodular transformations, i.e,
transformations with any value of their determinant at a point. Geometrically, they correspond to similarity
transformations, which preserve the shape but not the size of four-volumes in space-time. Usually, one
“compensates” for this unwanted change of size by introducing tensor densities: When appropriate weights
are introduced for various tensors, these densities can undo the effects of the size changes produced by
non-unimodular transformations.
However, one may simply start from 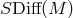 as the automorphism group. The action of its
stabilizer on the tangent space at each point of
as the automorphism group. The action of its
stabilizer on the tangent space at each point of 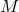 is
is 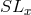 , the maximal symmetry group that
preserves the size of four-volumes, thus avoiding the need to introduce densities, among its many
other advantages (see Stachel, 2011
, the maximal symmetry group that
preserves the size of four-volumes, thus avoiding the need to introduce densities, among its many
other advantages (see Stachel, 2011 ; Bradonjić and Stachel, 2012
; Bradonjić and Stachel, 2012 ). For much of the following
discussion, however, the distinction between
). For much of the following
discussion, however, the distinction between 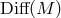 and
and  is inessential, so I shall
continue to discuss
is inessential, so I shall
continue to discuss 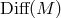 , and only point out the distinction at some places where it is really
important.
, and only point out the distinction at some places where it is really
important.
Symmetry transformations:
By definition,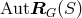 , the group of permutations of the points
of
, the group of permutations of the points
of 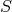 defining the geometry
defining the geometry 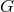 , leaves the relations
, leaves the relations 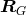 (which equally well define the
geometry of
(which equally well define the
geometry of 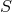 ) unchanged; so the
) unchanged; so the 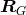 do not need to be permuted when the points of
do not need to be permuted when the points of 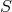 are.
Whichever Lie subgroup
are.
Whichever Lie subgroup 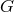 of
of 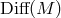 is chosen as the automorphism group defining the
geometry of a differentiable manifold
is chosen as the automorphism group defining the
geometry of a differentiable manifold 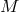 , similar comments hold for it. As we shall see, the
important difference for the hole argument is that between geometries based on finite-parameter
Lie groups and those based on Lie groups depending on one or more functions (functional Lie
groups).
, similar comments hold for it. As we shall see, the
important difference for the hole argument is that between geometries based on finite-parameter
Lie groups and those based on Lie groups depending on one or more functions (functional Lie
groups).
Passive coordinate transformations and the trivial identity:
Since it is no more than a re-labeling of its points, any admissible passive coordinate transformation has no effect on a geometry (see Section 4.1). However, if one restricts the group of coordinate transformations to a subgroup of those corresponding elements of the automorphism group of the geometry, then there is an isomorphism between this subgroup of passive coordinate transformations and the group of active point transformations defining the geometry. Hence, it is possible to reformulate any statement about the geometry in terms of relations between the coordinate components of the geometric object fields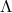 that are invariant under this subgroup of restricted coordinate
transformations. In the past, this is how coordinate-dependent techniques were used to arrive at geometric
results; and many contemporary treatments still utilize this technique. If one permutes the points
of
that are invariant under this subgroup of restricted coordinate
transformations. In the past, this is how coordinate-dependent techniques were used to arrive at geometric
results; and many contemporary treatments still utilize this technique. If one permutes the points
of  by a diffeomorphism, carries along the
by a diffeomorphism, carries along the 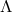 fields defining its geometry and the
fields defining its geometry and the 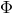 fields defining the theory, and also carries out the corresponding coordinate transformations,
then clearly the new fields at the new points will have the same coordinate components in the
new coordinate system as the old fields at the old points in the old coordinate system. This
observation is another, coordinate-dependent variant of the basic or trivial identity. It holds for
any
fields defining the theory, and also carries out the corresponding coordinate transformations,
then clearly the new fields at the new points will have the same coordinate components in the
new coordinate system as the old fields at the old points in the old coordinate system. This
observation is another, coordinate-dependent variant of the basic or trivial identity. It holds for
any 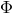 fields, quite independently of any theory, or any field equations that these fields may
obey.
fields, quite independently of any theory, or any field equations that these fields may
obey.
Basis vectors and a coordinate-independent formulation of the trivial identity:
Geometrically, a coordinate system corresponds to the choice of a holonomic basis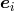 at each point of
at each point of 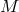 : That is, there is a local
coordinate system such that
: That is, there is a local
coordinate system such that 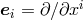 . But the essential element geometrically is the choice of a basis, not
its holonomicity. So, introduce an ordered set of basis vectors
. But the essential element geometrically is the choice of a basis, not
its holonomicity. So, introduce an ordered set of basis vectors 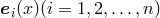 , holonomic or not, at
each point
, holonomic or not, at
each point 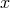 of
of 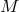 together with the associated dual basis of covectors or one-forms
together with the associated dual basis of covectors or one-forms 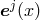 , such that
, such that
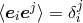 .53
Associated with the geometric object fields
.53
Associated with the geometric object fields 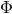 and
and 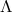 on
on 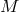 are their components with respect to such
a pair of basis vectors, which will be symbolized by
are their components with respect to such
a pair of basis vectors, which will be symbolized by ![Φ[e(x)]](article411x.gif) and
and ![Λ [e (x)]](article412x.gif) : This is a set of
coordinate-independent scalars that result from saturating all the free covariant and contravariant indices of
: This is a set of
coordinate-independent scalars that result from saturating all the free covariant and contravariant indices of
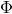 and
and 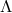 with the
with the 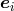 and
and 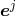 respectively.
Of course, under a change of basis:
respectively.
Of course, under a change of basis: 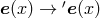 these scalars transform appropriately. A
diffeomorphism
these scalars transform appropriately. A
diffeomorphism 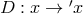 induces such a change of basis:
induces such a change of basis: 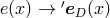 , and corresponding changes
in the geometric object fields
, and corresponding changes
in the geometric object fields 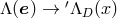 and
and 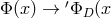 ). However, the values of these scalars
remain unchanged if one carries out the associated push forwards and pull backs of
). However, the values of these scalars
remain unchanged if one carries out the associated push forwards and pull backs of 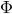 and
and 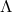 , as
well of the basis vectors and covectors. That is, if we take the new basis vectors at the new
point:
, as
well of the basis vectors and covectors. That is, if we take the new basis vectors at the new
point: 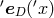 ; then the new components with respect to the new basis vectors at the new
points will equal the old components with respect to the old basis vectors at the old points:
; then the new components with respect to the new basis vectors at the new
points will equal the old components with respect to the old basis vectors at the old points:
![Φ [e (x)] = ′ΦD [′eD (′x )]](article425x.gif) and
and ![Λ [e(x)] = ′ΛD [′eD (′x )]](article426x.gif) . This observation is a coordinate-independent
formulation of the basic identity. Since any model of a physical theory can only fix the values
of such coordinate-independent scalars with respect to some basis for all geometric objects
in that model, this identity cannot fail to hold for any theory based on the
. This observation is a coordinate-independent
formulation of the basic identity. Since any model of a physical theory can only fix the values
of such coordinate-independent scalars with respect to some basis for all geometric objects
in that model, this identity cannot fail to hold for any theory based on the 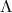 -geometry of
-geometry of
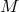 .
.
Covariance and general covariance:
Suppose we perform the push forwards and pull packs on the geometric object fields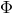 , but not on the
, but not on the 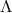 -geometry or the basis vectors and convectors.
That is, let
-geometry or the basis vectors and convectors.
That is, let 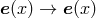 and
and ![Λ[e(x)] → Λ [e (x )]](article432x.gif) , but
, but ![′ Φ [e(x )] → ΦD [e(x)]](article433x.gif) . In general,
. In general,
![′ Φ [e (x)] ⁄= ΦD [e(x)]](article434x.gif) , so this results in a set of scalars that is distinct from
, so this results in a set of scalars that is distinct from ![Φ [e(x )]](article435x.gif) at each point
at each point 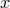 of
of
 .
A theory is covariant under the the
.
A theory is covariant under the the  -geometry’s automorphism group if, whenever
-geometry’s automorphism group if, whenever ![Φ [e (x)]](article439x.gif) is a
model of the theory, then so is
is a
model of the theory, then so is ![′Φ [e (x)] D](article440x.gif) . Covariance clearly defines an equivalence relation
between models of the theory; so covariance divides all models of a theory into equivalence
classes.54
. Covariance clearly defines an equivalence relation
between models of the theory; so covariance divides all models of a theory into equivalence
classes.54
A covariant theory is generally covariant under the 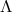 -geometry’s automorphism group if an entire
equivalence class of its mathematically distinct models corresponds to a single physical model of the
theory.
-geometry’s automorphism group if an entire
equivalence class of its mathematically distinct models corresponds to a single physical model of the
theory.
4.3 Fiber bundles: principal bundles, associated bundles, frame bundles, natural and gauge-natural bundles 55
An ordered set of basis vectors 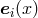 at a point of
at a point of 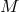 is called a linear frame, and the set of all such
linear frames at a point of
is called a linear frame, and the set of all such
linear frames at a point of 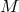 constitutes one fiber of the bundle of linear frames over
constitutes one fiber of the bundle of linear frames over 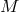 . As
Kobayashi explains, the bundle concept can be used to formulate any geometry on
. As
Kobayashi explains, the bundle concept can be used to formulate any geometry on 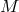 as a
as a
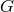 -structure:56
-structure:56
Let 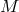 be a differentiable manifold of dimension
be a differentiable manifold of dimension 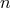 and
and 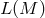 the bundle of linear
frames over
the bundle of linear
frames over  . Then
. Then 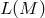 is the principal fibre bundle over
is the principal fibre bundle over 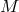 with group
with group
 . Let
. Let 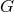 be a Lie subgroup of
be a Lie subgroup of 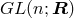 . By a
. By a  -structure on
-structure on 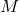 we shall mean a differentiable subbundle
we shall mean a differentiable subbundle 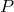 of
of 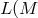 ) with structure group
) with structure group 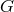 .
(Kobayashi, 1972, p. 1).
.
(Kobayashi, 1972, p. 1).
Such a fiber bundle formulation of geometries has several crucial advantages:
It makes evident the fundamental distinction between vertical geometrical quantities, such as metric
tensors, that live on the fibers of the bundle; and horizontal geometrical objects, such as linear affine
connections, that serve to connect these fibers. This is the case whether the metric and/or connection are
fixed and given components of 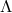 ; or are components of
; or are components of 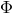 , themselves subject to dynamical field
equations.
, themselves subject to dynamical field
equations.
It enables us to go from global to local formulations of background-independent
theories, such as general relativity, in which the global topology of the base manifold
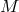 cannot be specified a priori, because it differs for different solutions to the field
equations.57
cannot be specified a priori, because it differs for different solutions to the field
equations.57
Fibered manifolds
The concept of fibered spaces for a set, discussed in Section 4.1, can now be applied to differentiable manifolds (see Section 4.2). After a fibered manifold is defined, the important cases of principal bundles, vector bundles, natural bundles and gauge-natural bundles and their physical applications are discussed, stressing the importance for general relativity of quotient bundles and local considerations.
A fibered manifold 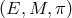 consists of a total manifold
consists of a total manifold 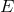 , a base manifold
, a base manifold 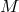 , and a projection
operator
, and a projection
operator 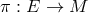 .
. 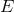 is a differentiable manifold, the points of which,
is a differentiable manifold, the points of which, 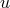 ,
,  , etc., are
grouped into fibers by an equivalence relation
, etc., are
grouped into fibers by an equivalence relation 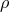 between its points.
between its points. 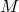 is also a differentiable
manifold, the points of which are symbolized by
is also a differentiable
manifold, the points of which are symbolized by  ,
, 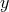 , etc. The fiber over
, etc. The fiber over 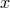 is symbolized by
is symbolized by
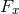 . Note that, if the relation
. Note that, if the relation 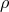 is given initially, sometimes the base manifold
is given initially, sometimes the base manifold 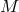 may be
defined as the quotient of the total manifold
may be
defined as the quotient of the total manifold 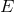 by
by 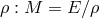 ; in other words as the
orbit space of
; in other words as the
orbit space of 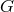 (see Sections 4.1 and 4.2). But the situation is generally somewhat more
complicated:
(see Sections 4.1 and 4.2). But the situation is generally somewhat more
complicated:
Usually, when symmetries and invariance groups are considered, a problem reduces to the corresponding orbit space, and therefore the structure of these spaces has to be investigated. This structure theory is quite complicated in general, since these spaces usually are singular spaces and not again manifolds. In fact, only if the action of the Lie group is free (i.e., all isotropy subgroups of single points are trivial), the resulting orbit space bears a manifold structure and forms together with the manifold and the quotient map a principal fiber bundle, whose structure is well known. More often, the orbit space admits a stratification into smooth manifolds with an open and dense largest stratum, the set of principal orbits…. This stratified space can then be treated almost like a manifold when taking special care. The existence of such a stratification is usually shown by proving the existence of slices at every point for the group action (Schichl, 1997, p. 1).
I shall assume that – as in general relativity – in any theory considered, the quotient space is either a manifold or a stratified manifold; and that any local solution to its field equations can be extended to a global solution.58
A fiber bundle is a fibered manifold in which all its fibers are isomorphic to a typical fiber 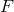 , itself a
manifold; that is, for all
, itself a
manifold; that is, for all 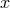 ,
, 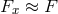 . Suppose
. Suppose 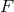 is
is 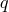 -dimensional and
-dimensional and 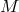 is
is 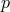 -dimensional One
can always introduce a local trivialization of the bundle: Let
-dimensional One
can always introduce a local trivialization of the bundle: Let  be an open subspace of
be an open subspace of 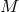 . Locally, the
total space
. Locally, the
total space 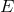 is a product space
is a product space 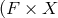 ), and one can introduce
), and one can introduce 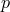 variables
variables 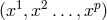 as local
coordinates of a point
as local
coordinates of a point 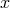 of
of 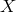 , and
, and 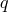 variables
variables 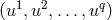 as coordinates of a point
as coordinates of a point 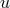 of
of 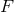 .
So
.
So 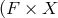 ) is coordinatized by the
) is coordinatized by the 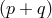 coordinates
coordinates 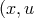 ) of a point
) of a point 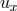 of
of 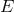 lying on
the fiber
lying on
the fiber 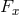 over the point
over the point 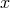 . Let
. Let 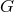 be a Lie group of diffeomorphisms that acts on
be a Lie group of diffeomorphisms that acts on
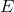 .59
The action of an element
.59
The action of an element 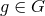 on the point
on the point 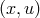 of
of 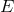 is symbolized by
is symbolized by
![(x,u ) → g(x,u ) = (′x,′u) = [χ(x,u),ψ (x,u)]](article524x.gif) .
.
Two subgroups of 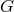 are especially important:
are especially important:
- The base transformations (diffeomorphisms of
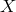 ) that do not affect the fibers:
) that do not affect the fibers:
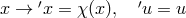 .
.
- The pure fiber or pure gauge transformations on the fiber at each point:
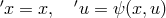 .
.
Both of these are included in a third subgroup:
- The fiber-preserving transformations:
![′ ′ (x,u) → (x, u) = [χ(x),ψ (x,u)]](article529x.gif) .
.
If 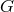 is a connected Lie group, all of its actions can be constructed from iterations of the action of its
Lie algebra, composed of its infinitesimal generators: The vector fields
is a connected Lie group, all of its actions can be constructed from iterations of the action of its
Lie algebra, composed of its infinitesimal generators: The vector fields 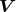 on
on 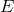 , each of which generates
a one-parameter group of point transformations, or flow, on
, each of which generates
a one-parameter group of point transformations, or flow, on 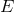 . Locally
. Locally  may be written in terms of
the coordinates
may be written in terms of
the coordinates 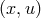 :
:
The generator 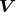 is called:
is called:
Horizontal if 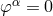 , i.e., it generates only base transformations.
, i.e., it generates only base transformations.
Vertical if 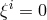 , i.e., if it generates only pure fiber or pure gauge transformations.
, i.e., if it generates only pure fiber or pure gauge transformations.
The flow generated by  will be fiber preserving if and only if
will be fiber preserving if and only if 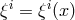 .
.
Natural bundles:
A fiber-preserving diffeomorphism projects naturally into a unique diffeomorphism of the base manifold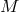 ; but generally the converse does not hold. If it does, i.e., if a base
diffeomorphism of
; but generally the converse does not hold. If it does, i.e., if a base
diffeomorphism of 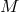 lifts uniquely to a fiber-preserving diffeomorphism of
lifts uniquely to a fiber-preserving diffeomorphism of  , then the
bundle is a natural bundle. A geometric object defined on such a bundle is called a natural
object.60
This is the fiber bundle version of the definition of geometric objects in Section 4.2.
, then the
bundle is a natural bundle. A geometric object defined on such a bundle is called a natural
object.60
This is the fiber bundle version of the definition of geometric objects in Section 4.2.
Principal bundles, associated vector bundles:
If the the typical fiber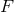 is isomorphic to the structure group
is isomorphic to the structure group 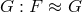 , then the bundle is a
principal fiber bundle
, then the bundle is a
principal fiber bundle 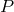 with structure group
with structure group 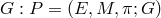 . Corresponding to any
. Corresponding to any 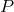 with
structure group
with
structure group 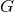 , there is a class of associated vector bundles. In such an associated bundle, each fiber
forms a vector representation of
, there is a class of associated vector bundles. In such an associated bundle, each fiber
forms a vector representation of 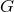 . This vector representation need not be irreducible, so the class of
associated vector bundles includes all tensor fields.
. This vector representation need not be irreducible, so the class of
associated vector bundles includes all tensor fields.
4.4 Covariance and general covariance for natural and gauge-natural bundles
The use of fibered manifolds allows a precise formulation of the concepts of covariance and general covariance for any physical theory; and of the hole argument for background-independent theories, and even – with appropriate modifications – for some partially-background-dependent theories.
4.4.1 Fiber bundles needed in physics
Every natural physical theory can be formulated in terms of some natural geometric
object(s)61 that lives on an appropriate
fibered differentiable manifold,62
the nature of which depends on these geometric object(s). If the theory is defined on a differentiable
manifold 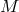 that is the quotient of the fibered manifold
that is the quotient of the fibered manifold 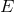 divided by the equivalence relation
divided by the equivalence relation 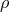 defining the fibration,
defining the fibration,  ; then there is an operator
; then there is an operator  , projecting each fiber onto the
corresponding point of
, projecting each fiber onto the
corresponding point of 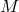 :
: 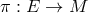 . Since the fibered manifold represents a natural object, there is a
one-one correspondence between fiber-preserving diffeomorphisms of
. Since the fibered manifold represents a natural object, there is a
one-one correspondence between fiber-preserving diffeomorphisms of 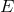 and diffeomorphisms of
and diffeomorphisms of
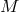 .
.
A number of most important gauge natural theories cannot be so formulated, but require the broader concept of gauge natural bundles for their precise formulation. Indeed, every classical physical theory can be reformulated as the jet prolongation of some gauge natural bundle by adjoining the derivatives of the geometric object fields to the original bundle.63
4.4.2 Background-dependent theories
A theory based on such fixed 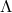 -fields on
-fields on 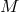 is called background-dependent, with
is called background-dependent, with 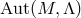 as its symmetry
group.64
Any geometric object fields
as its symmetry
group.64
Any geometric object fields 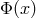 can then be introduced on this fixed-background space-time together
with a set of field equations governing their dynamics, which generally involve some or all of the
can then be introduced on this fixed-background space-time together
with a set of field equations governing their dynamics, which generally involve some or all of the
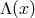 .
.
In many theories, the fixed geometric object fields on 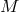 consist of a vertical chrono-geometric metric
tensor on each fiber and the corresponding horizontal inertio-gravitational linear connection. Any
non-gravitational theory can be formulated on a fiber bundle associated with the principal bundle
determined by the metric and connection: The
consist of a vertical chrono-geometric metric
tensor on each fiber and the corresponding horizontal inertio-gravitational linear connection. Any
non-gravitational theory can be formulated on a fiber bundle associated with the principal bundle
determined by the metric and connection: The 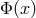 break up into two subclasses: The fields of massive
objects (such as charged bodies) are represented by geometric quantities living on the vertical fibers; and
the gauge fields transmitting the forces between these objects (such as the electromagnetic field) are
represented by verical connections along the fibers; these connections are only fixed up to some group of
gauge transformations.
break up into two subclasses: The fields of massive
objects (such as charged bodies) are represented by geometric quantities living on the vertical fibers; and
the gauge fields transmitting the forces between these objects (such as the electromagnetic field) are
represented by verical connections along the fibers; these connections are only fixed up to some group of
gauge transformations.
4.4.3 Background-independent theories
In the case of general relativity and other background-independent theories (such as the coupled
Einstein–Maxwell equations), 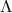 reduces to the identity and there are no fixed background space-time
structures on
reduces to the identity and there are no fixed background space-time
structures on 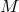 .
. 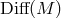 is chosen as
is chosen as 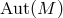 in the usual formulations; but, as suggested in
Section 4.2,
in the usual formulations; but, as suggested in
Section 4.2, 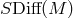 , the unimodular subgroup, may be chosen. In that case, the space-time structures
subdivide further: The pseudo-metric splits into a conformal metric with determinant
, the unimodular subgroup, may be chosen. In that case, the space-time structures
subdivide further: The pseudo-metric splits into a conformal metric with determinant 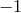 and a scalar field, both of which live on the vertical fibers; while the linear affine connection
splits into a trace-free projective connection and a one form, both of which serve to connect the
fibers.
and a scalar field, both of which live on the vertical fibers; while the linear affine connection
splits into a trace-free projective connection and a one form, both of which serve to connect the
fibers.
4.4.4 Gauge symmetries
To define the gauge symmetries of a certain type of theory, one must consider the sections of the
corresponding fiber bundle. A local section 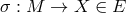 or global cross section
or global cross section 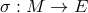 is a map
taking each point
is a map
taking each point 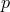 of
of 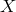 or
or 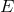 , respectively, into a unique point of the fiber
, respectively, into a unique point of the fiber 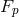 over
over
 .65
.65
For each type of physical theory, a section represents a particular configuration of the corresponding
physical field. However, in theories of the gauge-field type, this representation is not unique. There is a
group of gauge transformations, each element of which maps one mathematical representative of some field
configuration into another representative of the same configuration. A gauge symmetry is an equivalence
relation on the set of sections: Two sections 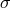 and
and 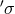 are gauge equivalent if there is a
gauge transformation taking one into the other. This equivalence relation divides the set of
all sections into equivalence classes, the gauge orbits; each section belongs to one and only
one such orbit. If the gauge group of some type of theory consists entirely of fiber-preserving
transformations, then the theory can be formulated on a natural bundle. But if its gauge group includes
non-fiber-preserving transformations, then a gauge-natural bundle is needed to formulate this type of theory
correctly.
are gauge equivalent if there is a
gauge transformation taking one into the other. This equivalence relation divides the set of
all sections into equivalence classes, the gauge orbits; each section belongs to one and only
one such orbit. If the gauge group of some type of theory consists entirely of fiber-preserving
transformations, then the theory can be formulated on a natural bundle. But if its gauge group includes
non-fiber-preserving transformations, then a gauge-natural bundle is needed to formulate this type of theory
correctly.
The field equations of a particular gauge field theory serve to pick out a class of preferred
sections consisting of the solutions to these equations. For a gauge theory, these equations
must be of such a form that, if one section is a solution, then so are all members of the entire
gauge orbit of that section. In other words, the gauge transformations must form a symmetry
group of the field equations. This group is the automorphism group 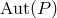 of the principal
gauge-natural bundle
of the principal
gauge-natural bundle 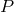 corresponding to the theory (see, e.g., Fatibene and Francaviglia, 2003,
p. 223). Fatibene and his collaborators explain the distinction between the two types of theory
well:
corresponding to the theory (see, e.g., Fatibene and Francaviglia, 2003,
p. 223). Fatibene and his collaborators explain the distinction between the two types of theory
well:
The main technical difference between natural and gauge natural theories is that [base]
diffeomorphisms are completely replaced by gauge transformations. In gauge natural
theories spacetime diffeomorphisms do not act at all on fields, since the only action
one can define in general is that of gauge transformations. This is due to the fact
that although pure gauge transformations are canonically embedded into the group of
generalized gauge transformations, there is no canonical “horizontal” complement to be
identified with 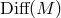 . …“Horizontal” symmetries, in fact, are generally associated to
physically relevant conservation laws, such as energy, momentum and angular momentum.
The definition of such quantities is almost trivial in natural theories; on the contrary, in
gauge natural theories pure gauge transformations are easily associated to gauge charges
(e.g., the electric charge in electromagnetism), while the absence of “horizontal” gauge
transformations is a problem to be solved to appropriately define energy, momentum and
angular momentum. For this reason, in gauge natural theories the dynamical connection
plays an extra role in determining horizontal infinitesimal symmetries as the gauge
generators which are horizontal with respect to the principal connection (Fatibene et al.,
2001, pp. 3–4).
. …“Horizontal” symmetries, in fact, are generally associated to
physically relevant conservation laws, such as energy, momentum and angular momentum.
The definition of such quantities is almost trivial in natural theories; on the contrary, in
gauge natural theories pure gauge transformations are easily associated to gauge charges
(e.g., the electric charge in electromagnetism), while the absence of “horizontal” gauge
transformations is a problem to be solved to appropriately define energy, momentum and
angular momentum. For this reason, in gauge natural theories the dynamical connection
plays an extra role in determining horizontal infinitesimal symmetries as the gauge
generators which are horizontal with respect to the principal connection (Fatibene et al.,
2001, pp. 3–4).
While bundle formulations of the hole argument originally dealt only with natural bundles, Lyre (1999 )
develops a generalized version that can be applied to gauge-natural bundles:
)
develops a generalized version that can be applied to gauge-natural bundles:
The generalized hole argument is motivated and extended from the spacetime hole argument …. [It] rules out fiber bundle substantivalism and, thus, a relationalistic interpretation of the geometry of fiber bundles is favored (Lyre, 1999, p. 1).
Healey (2001) also argues that “fiber bundle substantivalism …is subject to an analogue of the ‘hole’ argument against space-time substantivalism.”
4.4.5 Four-geometries and stratified manifolds
To recapitulate: The choice of a bundle 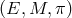 selects a certain type of physical theory but does not
picked out a particular theory of that type, nor introduce any space-time structures on
selects a certain type of physical theory but does not
picked out a particular theory of that type, nor introduce any space-time structures on 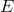 or
or 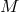 . The
points of
. The
points of 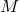 form a geometry (see Section 4.1). As points of the space-time manifold, they have
quiddity but they lack haecceity: a priori there is nothing to distinguish one such point from the
others. Their automorphism group is the diffeomorphism group of
form a geometry (see Section 4.1). As points of the space-time manifold, they have
quiddity but they lack haecceity: a priori there is nothing to distinguish one such point from the
others. Their automorphism group is the diffeomorphism group of 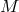 or some appropriate
subgroup, such as the unimodular group (see Stachel, 2011
or some appropriate
subgroup, such as the unimodular group (see Stachel, 2011 ; Bradonjić and Stachel, 2012
; Bradonjić and Stachel, 2012 ).
For example, a metric-free formulation of electromagnetic theory can be based on a bundle of
one-forms.
).
For example, a metric-free formulation of electromagnetic theory can be based on a bundle of
one-forms.
A particular theory is a rule for choosing a preferred class of cross sections of the fiber bundle. This rule
generally includes specification of some space-time structures on 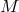 . For example, in addition to a bundle
of one-forms, source-free Maxwell electromagnetic theory, requires the specification of a conformal structure
on
. For example, in addition to a bundle
of one-forms, source-free Maxwell electromagnetic theory, requires the specification of a conformal structure
on 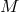 .
.
In general relativity, an equivalence class of diffeomorphically-equivalent pseudo-metrics on a four-dimensional
manifold,66
often referred to as a four-geometry, is regarded as corresponding to a single inertia-gravitational
field. While the fiber space consisting of all four-metrics over a given manifold forms a
manifold,67
the space of all four-geometries does not form a simple manifold, but a stratified manifold. That is, it is
partitioned into slices, each of which is itself a manifold, consisting of all four-geometries having the same
symmetry or isometry group. The largest slice is the manifold of generic geometries having no nontrivial
symmetries; it contains the vast majority of geometries. Thence one descends slice by slice down to the slice
consisting of all four-geometries having the maximal symmetry group (see Stachel, 2009 and
Section 6.1).
and
Section 6.1).
The rule specifying the choice of a preferred class of space time structures may or may
not include some restriction on 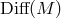 , the maximal possible automorphism group of
, the maximal possible automorphism group of
 . Obviously, diffeomorphisms always remain unrestricted in the sense of the trivial
identity. A true restriction on the theory arises with the imposition of a finite-parameter
Lie group as the symmetry group of the class of space-time structures picked out by the
rule.68
If there are no such restrictions, the theory is background independent. If the rule includes a Lie group
involving some functions as well as parameters, the theory is partially background dependent. If the Lie
group is maximal (ten-parameters in four dimensions), then the theory is totally background dependent. If
the rule restricts the preferred class maximally, i.e., to the identity, then the theory specifies an
individuating field on the space-time, turning it into an algebra. In this formulation, the symmetry group is
included in the rule defining a physical theory, rather than being imposed a priori on the space-time
structures defined on
. Obviously, diffeomorphisms always remain unrestricted in the sense of the trivial
identity. A true restriction on the theory arises with the imposition of a finite-parameter
Lie group as the symmetry group of the class of space-time structures picked out by the
rule.68
If there are no such restrictions, the theory is background independent. If the rule includes a Lie group
involving some functions as well as parameters, the theory is partially background dependent. If the Lie
group is maximal (ten-parameters in four dimensions), then the theory is totally background dependent. If
the rule restricts the preferred class maximally, i.e., to the identity, then the theory specifies an
individuating field on the space-time, turning it into an algebra. In this formulation, the symmetry group is
included in the rule defining a physical theory, rather than being imposed a priori on the space-time
structures defined on 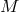 . This change enlarges the class of physical solutions: For example, not fixing the
global topology of
. This change enlarges the class of physical solutions: For example, not fixing the
global topology of 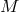 allows several possibilities for the global topology associated with a given local
metric. But this does not alter the fact that the symmetry group of the space-time structures
must be preserved by all such solutions. To what extent the hole argument applies to a non
background-independent theory depends on the degree of background dependence that has been imposed
(see Stachel, 2009
allows several possibilities for the global topology associated with a given local
metric. But this does not alter the fact that the symmetry group of the space-time structures
must be preserved by all such solutions. To what extent the hole argument applies to a non
background-independent theory depends on the degree of background dependence that has been imposed
(see Stachel, 2009 ); but if a theory is background independent, the hole argument certainly
applies.
); but if a theory is background independent, the hole argument certainly
applies.