7 Conclusion: The Hole Argument Redivivus
The problem becomes even more delicate for quantum systems, in which the existence of the quantum of action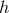 is taken into account. The finite value of
is taken into account. The finite value of 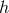 precludes the measurement of a complete set of
classical observables by a single compound procedure. It becomes important to show that a complete set of
quantum observables, as defined by the theory, can indeed be so measured in principle. Non-relativistic
quantum mechanics and quantum electrodynamics, have been show to meet this criterion; and it has been
employed as a test of proposals for what should be the fundamental physical quantities defined
in quantum gravity (see Bergmann and Smith, 1982; Amelino-Camelia and Stachel, 2009).
Rovelli (2004
precludes the measurement of a complete set of
classical observables by a single compound procedure. It becomes important to show that a complete set of
quantum observables, as defined by the theory, can indeed be so measured in principle. Non-relativistic
quantum mechanics and quantum electrodynamics, have been show to meet this criterion; and it has been
employed as a test of proposals for what should be the fundamental physical quantities defined
in quantum gravity (see Bergmann and Smith, 1982; Amelino-Camelia and Stachel, 2009).
Rovelli (2004 ) and Oeckl (2008, 2013) have shown how to define such measurements on the
hypersurface bounding a four-dimensional region of space-time, even in a background-independent
theory.
) and Oeckl (2008, 2013) have shown how to define such measurements on the
hypersurface bounding a four-dimensional region of space-time, even in a background-independent
theory.
In field theory, the analog of the data set 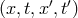 is the couple
is the couple ![[Σ,φ ]](article813x.gif) , where
, where 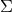 is
a 3d surface bounding a finite spacetime region, and
is
a 3d surface bounding a finite spacetime region, and 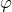 is a field configuration on
is a field configuration on 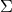 .
…The data from a local experiment (measurements, preparation, or just assumptions)
must in fact refer to the state of the system on the entire boundary of a finite spacetime
region. The field theoretical space
.
…The data from a local experiment (measurements, preparation, or just assumptions)
must in fact refer to the state of the system on the entire boundary of a finite spacetime
region. The field theoretical space  is therefore the space of surfaces
is therefore the space of surfaces 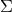 and
field configurations
and
field configurations 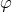 on
on 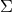 . Quantum dynamics can be expressed in terms of an
[probability] amplitude
. Quantum dynamics can be expressed in terms of an
[probability] amplitude ![W [Σ, φ]](article821x.gif) . Following Feynman’s intuition, we can formally define
. Following Feynman’s intuition, we can formally define
![W [Σ, φ]](article822x.gif) in terms of a sum over bulk field configurations that take the value
in terms of a sum over bulk field configurations that take the value 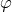 on
the boundary
on
the boundary 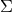 . …Notice that the dependence of
. …Notice that the dependence of ![W [Σ,φ ]](article825x.gif) on the geometry of
on the geometry of 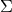 codes the spacetime position of the measuring apparatus. In fact, the relative position
of the components of the apparatus is determined by their physical distance and the
physical time elapsed between measurements, and these data are contained in the metric
of
codes the spacetime position of the measuring apparatus. In fact, the relative position
of the components of the apparatus is determined by their physical distance and the
physical time elapsed between measurements, and these data are contained in the metric
of 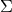 . …What is happening is that in background-dependent QFT we have two kinds of
measurements: those that determine the distances of the parts of the apparatus and the
time elapsed between measurements, and the actual measurements of the fields’ dynamical
variables. In quantum gravity, instead, distances and time separations are on an equal
footing with the dynamical fields. This is the core of the general relativistic revolution,
and the key for background-independent QFT (Rovelli, 2004, p. 23).
. …What is happening is that in background-dependent QFT we have two kinds of
measurements: those that determine the distances of the parts of the apparatus and the
time elapsed between measurements, and the actual measurements of the fields’ dynamical
variables. In quantum gravity, instead, distances and time separations are on an equal
footing with the dynamical fields. This is the core of the general relativistic revolution,
and the key for background-independent QFT (Rovelli, 2004, p. 23).
In this sense, Einstein’s hole, as a symbol of process, has reasserted its physical primacy over Hilbert’s Cauchy surface, as a symbol of instantaneous state (see Section 2.7).