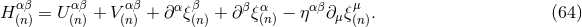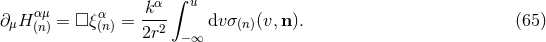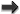2 Non-linear Iteration of the Vacuum Field Equations
2.1 Einstein’s field equations
The field equations of general relativity are obtained by varying the space-time metric 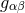 in the famous
Einstein–Hilbert action,
in the famous
Einstein–Hilbert action,
 is generated, through the gravitational coupling
constant
is generated, through the gravitational coupling
constant 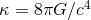 , by the stress-energy tensor
, by the stress-energy tensor 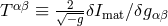 of the matter fields
of the matter fields 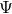 .
Among these ten equations, four govern, via the contracted Bianchi identity, the evolution of the matter
system,
The matter equations can also be obtained by varying the matter action in (17*) with respect to the matter
fields
.
Among these ten equations, four govern, via the contracted Bianchi identity, the evolution of the matter
system,
The matter equations can also be obtained by varying the matter action in (17*) with respect to the matter
fields 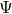 . The space-time geometry is constrained by the six remaining equations, which place six
independent constraints on the ten components of the metric
. The space-time geometry is constrained by the six remaining equations, which place six
independent constraints on the ten components of the metric 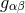 , leaving four of them to be fixed by a
choice of the coordinate system.
, leaving four of them to be fixed by a
choice of the coordinate system.
In most of this paper we adopt the conditions of harmonic coordinates, sometimes also called de Donder coordinates. We define, as a basic variable, the gravitational-field amplitude
where denotes the contravariant metric (satisfying
denotes the contravariant metric (satisfying  ), where
), where  is the
determinant of the covariant metric,
is the
determinant of the covariant metric, 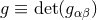 , and where
, and where 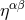 represents an auxiliary
Minkowskian metric
represents an auxiliary
Minkowskian metric 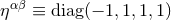 . The harmonic-coordinate condition, which accounts
exactly for the four equations (19*) corresponding to the conservation of the matter tensor,
reads13
Equation (21*) introduces into the definition of our coordinate system a preferred Minkowskian structure,
with Minkowski metric
. The harmonic-coordinate condition, which accounts
exactly for the four equations (19*) corresponding to the conservation of the matter tensor,
reads13
Equation (21*) introduces into the definition of our coordinate system a preferred Minkowskian structure,
with Minkowski metric 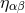 . Of course, this is not contrary to the spirit of general relativity, where there is
only one physical metric
. Of course, this is not contrary to the spirit of general relativity, where there is
only one physical metric 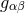 without any flat prior geometry, because the coordinates are not
governed by geometry (so to speak), but rather can be chosen at convenience, depending on
physical phenomena under study. The coordinate condition (21*) is especially useful when studying
gravitational waves as perturbations of space-time propagating on the fixed background metric
without any flat prior geometry, because the coordinates are not
governed by geometry (so to speak), but rather can be chosen at convenience, depending on
physical phenomena under study. The coordinate condition (21*) is especially useful when studying
gravitational waves as perturbations of space-time propagating on the fixed background metric
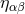 . This view is perfectly legitimate and represents a fruitful and rigorous way to think of
the problem using approximation methods. Indeed, the metric
. This view is perfectly legitimate and represents a fruitful and rigorous way to think of
the problem using approximation methods. Indeed, the metric  , originally introduced
in the coordinate condition (21*), does exist at any finite order of approximation (neglecting
higher-order terms), and plays the role of some physical “prior” flat geometry at any order of
approximation.
, originally introduced
in the coordinate condition (21*), does exist at any finite order of approximation (neglecting
higher-order terms), and plays the role of some physical “prior” flat geometry at any order of
approximation.
The Einstein field equations in harmonic coordinates can be written in the form of inhomogeneous flat d’Alembertian equations,
where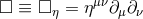 . The source term
. The source term  can rightly be interpreted as the stress-energy
pseudo-tensor (actually,
can rightly be interpreted as the stress-energy
pseudo-tensor (actually, 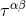 is a Lorentz-covariant tensor) of the matter fields, described by
is a Lorentz-covariant tensor) of the matter fields, described by 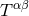 , and
the gravitational field, given by the gravitational source term
, and
the gravitational field, given by the gravitational source term  , i.e.,
The exact expression of
, i.e.,
The exact expression of 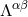 in harmonic coordinates, including all non-linearities,
reads14
in harmonic coordinates, including all non-linearities,
reads14
As is clear from this expression, 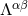 is made of terms at least quadratic in the gravitational-field
strength
is made of terms at least quadratic in the gravitational-field
strength 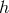 and its first and second space-time derivatives. In the following, for the highest
post-Newtonian order that we shall consider, we will need the quadratic, cubic and quartic pieces of
and its first and second space-time derivatives. In the following, for the highest
post-Newtonian order that we shall consider, we will need the quadratic, cubic and quartic pieces of 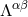 ;
with obvious notation, we can write them as
;
with obvious notation, we can write them as
As we said, the condition (21*) is equivalent to the matter equations of motion, in the sense of the
conservation of the total pseudo-tensor 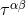 ,
,
- The matter stress-energy tensor
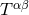 is of spatially compact support, i.e., can be enclosed into some
time-like world tube, say
is of spatially compact support, i.e., can be enclosed into some
time-like world tube, say 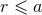 , where
, where 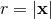 is the harmonic-coordinate radial distance. Outside
the domain of the source, when
is the harmonic-coordinate radial distance. Outside
the domain of the source, when 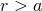 , the gravitational source term, according to Eq. (27*), is
divergence-free,
, the gravitational source term, according to Eq. (27*), is
divergence-free,
- The matter distribution inside the source is smooth:
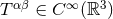 .16
We have in mind a smooth hydrodynamical fluid system, without any singularities nor shocks (a
priori), that is described by some Euler-type equations including high relativistic corrections.
In particular, we exclude from the start the presence of any black holes; however, we
shall return to this question in Part B when we look for a model describing compact
objects;
.16
We have in mind a smooth hydrodynamical fluid system, without any singularities nor shocks (a
priori), that is described by some Euler-type equations including high relativistic corrections.
In particular, we exclude from the start the presence of any black holes; however, we
shall return to this question in Part B when we look for a model describing compact
objects;
- The source is post-Newtonian in the sense of the existence of the small parameter defined by Eq. (1*). For such a source we assume the legitimacy of the method of matched asymptotic expansions for identifying the inner post-Newtonian field and the outer multipolar decomposition in the source’s exterior near zone;
- The gravitational field has been independent of time (stationary) in some remote past, i.e., before
some finite instant
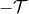 in the past, namely
in the past, namely
The latter condition is a means to impose, by brute force, the famous no-incoming radiation condition,
ensuring that the matter source is isolated from the rest of the Universe and does not receive any radiation
from infinity. Ideally, the no-incoming radiation condition should be imposed at past null infinity. As we
shall see, this condition entirely fixes the radiation reaction forces inside the isolated source. We shall later
argue (see Section 3.2) that our condition of stationarity in the past (29*), although weaker than the ideal
no-incoming radiation condition, does not entail any physical restriction on the general validity of the
formulas we derive. Even more, the condition (29*) is actually better suited in the case of real
astrophysical sources like inspiralling compact binaries, for which we do not know the details of the
initial formation and remote past evolution. In practice the initial instant 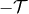 can be set
right after the explosions of the two supernovæ yielding the formation of the compact binary
system.
can be set
right after the explosions of the two supernovæ yielding the formation of the compact binary
system.
Subject to the past-stationarity condition (29*), the differential equations (22*) can be written equivalently into the form of the integro-differential equations
containing the usual retarded inverse d’Alembertian integral operator, given by extending over the whole three-dimensional space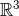 .
.
2.2 Linearized vacuum equations
In what follows we solve the field equations (21*) – (22*), in the vacuum region outside the compact-support
source, in the form of a formal non-linearity or post-Minkowskian expansion, considering the field variable
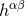 as a non-linear metric perturbation of Minkowski space-time. At the linearized level (or
first-post-Minkowskian approximation), we write:
as a non-linear metric perturbation of Minkowski space-time. At the linearized level (or
first-post-Minkowskian approximation), we write:
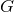 as a book-keeping parameter, enabling one to label conveniently
the successive post-Minkowskian approximations. Since
as a book-keeping parameter, enabling one to label conveniently
the successive post-Minkowskian approximations. Since 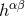 is a dimensionless variable, with our
convention the linear coefficient
is a dimensionless variable, with our
convention the linear coefficient 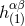 in Eq. (32*) has the dimension of the inverse of
in Eq. (32*) has the dimension of the inverse of 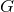 (which should be
a mass squared in a system of units where
(which should be
a mass squared in a system of units where 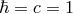 ). In vacuum, the harmonic-coordinate metric
coefficient
). In vacuum, the harmonic-coordinate metric
coefficient 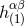 satisfies
satisfies
We want to solve those equations by means of an infinite multipolar series valid outside a time-like world
tube containing the source. Indeed the multipole expansion is the appropriate method for describing the
physics of the source as seen from its exterior (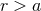 ). On the other hand, the post-Minkowskian series is
physically valid in the weak-field region, which surely includes the exterior of any source, starting at a
sufficiently large distance. For post-Newtonian sources the exterior weak-field region, where both multipole
and post-Minkowskian expansions are valid, simply coincides with the exterior region
). On the other hand, the post-Minkowskian series is
physically valid in the weak-field region, which surely includes the exterior of any source, starting at a
sufficiently large distance. For post-Newtonian sources the exterior weak-field region, where both multipole
and post-Minkowskian expansions are valid, simply coincides with the exterior region 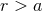 . It is
therefore quite natural, and even, one would say inescapable when considering general sources, to combine
the post-Minkowskian approximation with the multipole decomposition. This is the original idea of the
“double-expansion” series of Bonnor and collaborators [94, 95, 96, 251], which combines the
. It is
therefore quite natural, and even, one would say inescapable when considering general sources, to combine
the post-Minkowskian approximation with the multipole decomposition. This is the original idea of the
“double-expansion” series of Bonnor and collaborators [94, 95, 96, 251], which combines the
 -expansion (or
-expansion (or 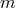 -expansion in their notation) with the
-expansion in their notation) with the  -expansion (equivalent to the
multipole expansion, since the
-expansion (equivalent to the
multipole expansion, since the 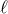 -th order multipole moment scales with the source radius like
-th order multipole moment scales with the source radius like
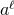 ).
).
The multipolar-post-Minkowskian (MPM) method will be implemented systematically, using symmetric-trace-free (STF) harmonics to describe the multipole expansion [403*], and looking for a definite algorithm for the approximation scheme [57*]. The solution of the system of equations (33) takes the form of a series of retarded multipolar waves17
where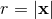 , and where the functions
, and where the functions 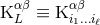 are smooth functions of the retarded time
are smooth functions of the retarded time
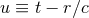 [i.e.,
[i.e., 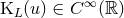 ], which become constant in the past, when
], which become constant in the past, when 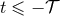 , see Eq. (29*).
Since a monopolar wave satisfies
, see Eq. (29*).
Since a monopolar wave satisfies 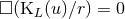 and the d’Alembertian commutes with the
multi-derivative
and the d’Alembertian commutes with the
multi-derivative 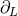 , it is evident that Eq. (34*) represents the most general solution of the wave
equation (33a); but see Section 2 in Ref. [57*] for a rigorous proof based on the Euler–Poisson–Darboux
equation. The gauge condition (33b), however, is not fulfilled in general, and to satisfy it we must
algebraically decompose the set of functions
, it is evident that Eq. (34*) represents the most general solution of the wave
equation (33a); but see Section 2 in Ref. [57*] for a rigorous proof based on the Euler–Poisson–Darboux
equation. The gauge condition (33b), however, is not fulfilled in general, and to satisfy it we must
algebraically decompose the set of functions 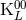 ,
, 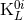 ,
, 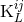 into ten tensors which are STF with
respect to all their indices, including the spatial indices
into ten tensors which are STF with
respect to all their indices, including the spatial indices 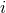 ,
, 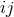 . Imposing the condition (33b) reduces the
number of independent tensors to six, and we find that the solution takes an especially simple
“canonical” form, parametrized by only two moments, plus some arbitrary linearized gauge
transformation [403*, 57*].
. Imposing the condition (33b) reduces the
number of independent tensors to six, and we find that the solution takes an especially simple
“canonical” form, parametrized by only two moments, plus some arbitrary linearized gauge
transformation [403*, 57*].
Theorem 1. The most general solution of the linearized field equations (33) outside some
time-like world tube enclosing the source ( ), and stationary in the past [see Eq. (29*)], reads
), and stationary in the past [see Eq. (29*)], reads
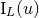 and
and 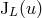 , which are arbitrary
functions of time except for the laws of conservation of the monopole:
, which are arbitrary
functions of time except for the laws of conservation of the monopole: 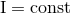 , and dipoles:
, and dipoles:
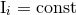 ,
,  . It is given by
. It is given by
The other terms represent a linearized gauge transformation, with gauge vector 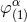 parametrized by
four other multipole moments, say
parametrized by
four other multipole moments, say 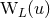 ,
, 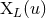 ,
, 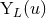 and
and 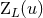 [see Eqs. (37)].
[see Eqs. (37)].
The conservation of the lowest-order moments gives the constancy of the total mass of the
source, 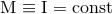 , center-of-mass position,
, center-of-mass position, 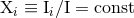 , total linear momentum
, total linear momentum
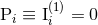 ,18
and total angular momentum,
,18
and total angular momentum, 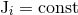 . It is always possible to achieve
. It is always possible to achieve 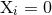 by translating the
origin of our coordinates to the center of mass. The total mass
by translating the
origin of our coordinates to the center of mass. The total mass 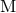 is the ADM mass of the Hamiltonian
formulation of general relativity. Note that the quantities
is the ADM mass of the Hamiltonian
formulation of general relativity. Note that the quantities 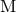 ,
, 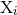 ,
, 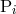 and
and 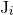 include the
contributions due to the waves emitted by the source. They describe the initial state of the source, before
the emission of gravitational radiation.
include the
contributions due to the waves emitted by the source. They describe the initial state of the source, before
the emission of gravitational radiation.
The multipole functions 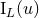 and
and  , which thoroughly encode the physical properties of the
source at the linearized level (because the other moments
, which thoroughly encode the physical properties of the
source at the linearized level (because the other moments  parametrize a gauge
transformation), will be referred to as the mass-type and current-type source multipole moments. Beware,
however, that at this stage the moments are not specified in terms of the stress-energy tensor
parametrize a gauge
transformation), will be referred to as the mass-type and current-type source multipole moments. Beware,
however, that at this stage the moments are not specified in terms of the stress-energy tensor 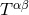 of the
source: Theorem 1 follows merely from the algebraic and differential properties of the vacuum field
equations outside the source.
of the
source: Theorem 1 follows merely from the algebraic and differential properties of the vacuum field
equations outside the source.
For completeness, we give the components of the gauge-vector 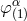 entering Eq. (35*):
entering Eq. (35*):
Because the theory is covariant with respect to non-linear diffeomorphisms and not merely with respect
to linear gauge transformations, the moments 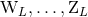 do play a physical role starting at the
non-linear level, in the following sense. If one takes these moments equal to zero and continues the
post-Minkowskian iteration [see Section 2.3] one ends up with a metric depending on
do play a physical role starting at the
non-linear level, in the following sense. If one takes these moments equal to zero and continues the
post-Minkowskian iteration [see Section 2.3] one ends up with a metric depending on  and
and 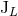 only, but that metric will not describe the same physical source as the one which would have
been constructed starting from the six moments
only, but that metric will not describe the same physical source as the one which would have
been constructed starting from the six moments 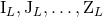 altogether. In other words, the
two non-linear metrics associated with the sets of multipole moments
altogether. In other words, the
two non-linear metrics associated with the sets of multipole moments 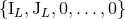 and
and
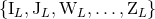 are not physically equivalent – they are not isometric. We shall point out
in Section 2.4 below that the full set of moments
are not physically equivalent – they are not isometric. We shall point out
in Section 2.4 below that the full set of moments 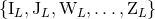 is in fact physically
equivalent to some other reduced set of moments
is in fact physically
equivalent to some other reduced set of moments 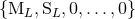 , but with some moments
, but with some moments
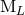 ,
, 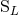 that differ from
that differ from 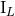 ,
, 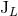 by non-linear corrections [see Eqs. (97) – (98)]. The
moments
by non-linear corrections [see Eqs. (97) – (98)]. The
moments 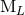 ,
, 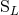 are called “canonical” moments; they play a useful role in intermediate
calculations. All the multipole moments
are called “canonical” moments; they play a useful role in intermediate
calculations. All the multipole moments 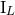 ,
, 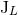 ,
, 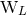 ,
, 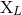 ,
, 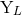 ,
,  will be computed in
Section 4.4.
will be computed in
Section 4.4.
2.3 The multipolar post-Minkowskian solution
By Theorem 1 we know the most general solution of the linearized equations in the exterior of the source. We then tackle the problem of the post-Minkowskian iteration of that solution. We consider the full post-Minkowskian series
where the first term is composed of the result given by Eqs. (35*) – (37). In this article, we shall always understand the infinite sums such as the one in Eq. (38*) in the sense of formal power series, i.e., as an ordered collection of coefficients,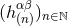 . We do not attempt to control the mathematical nature of the
series and refer to the mathematical-physics literature for discussion of that point (see, in the present
context, Refs. [130, 171, 361, 362*, 363]).
. We do not attempt to control the mathematical nature of the
series and refer to the mathematical-physics literature for discussion of that point (see, in the present
context, Refs. [130, 171, 361, 362*, 363]).
We substitute the post-Minkowski ansatz (38*) into the vacuum Einstein field equations (21*) – (22*), i.e.,
with 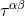 simply given by the gravitational source term
simply given by the gravitational source term 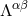 , and we equate term by term the factors of
the successive powers of our book-keeping parameter
, and we equate term by term the factors of
the successive powers of our book-keeping parameter 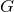 . We get an infinite set of equations for each of the
. We get an infinite set of equations for each of the
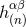 ’s: namely,
’s: namely, 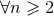 ,
,
The right-hand side of the wave equation (39a) is obtained from inserting the previous iterations, known
up to the order  , into the gravitational source term. In more details, the series of equations (39a)
reads
, into the gravitational source term. In more details, the series of equations (39a)
reads
The quadratic, cubic and quartic pieces of 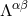 are defined by Eq. (25*) – (26).
are defined by Eq. (25*) – (26).
Let us now proceed by induction. Some 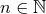 being given, we assume that we succeeded in
constructing, starting from the linearized solution
being given, we assume that we succeeded in
constructing, starting from the linearized solution 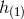 , the sequence of post-Minkowskian solutions
, the sequence of post-Minkowskian solutions
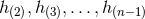 , and from this we want to infer the next solution
, and from this we want to infer the next solution 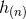 . The right-hand side of
Eq. (39a),
. The right-hand side of
Eq. (39a), 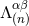 , is known by induction hypothesis. Thus the problem is that of solving a flat
wave equation whose source is given. The point is that this wave equation, instead of being
valid everywhere in
, is known by induction hypothesis. Thus the problem is that of solving a flat
wave equation whose source is given. The point is that this wave equation, instead of being
valid everywhere in 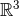 , is physically correct only outside the matter source (
, is physically correct only outside the matter source (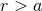 ), and
it makes no sense to solve it by means of the usual retarded integral. Technically speaking,
the right-hand side of Eq. (39a) is composed of the product of many multipole expansions,
which are singular at the origin of the spatial coordinates
), and
it makes no sense to solve it by means of the usual retarded integral. Technically speaking,
the right-hand side of Eq. (39a) is composed of the product of many multipole expansions,
which are singular at the origin of the spatial coordinates 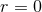 , and which make the retarded
integral divergent at that point. This does not mean that there are no solutions to the wave
equation, but simply that the retarded integral does not constitute the appropriate solution in that
context.
, and which make the retarded
integral divergent at that point. This does not mean that there are no solutions to the wave
equation, but simply that the retarded integral does not constitute the appropriate solution in that
context.
What we need is a solution which takes the same structure as the source term 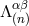 , i.e., is expanded
into multipole contributions, with a singularity at
, i.e., is expanded
into multipole contributions, with a singularity at 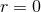 , and satisfies the d’Alembertian
equation as soon as
, and satisfies the d’Alembertian
equation as soon as 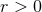 . Such a particular solution can be obtained, following the
method of Ref. [57*], by means of a mathematical trick, in which one first “regularizes” the
source term
. Such a particular solution can be obtained, following the
method of Ref. [57*], by means of a mathematical trick, in which one first “regularizes” the
source term 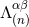 by multiplying it by the factor
by multiplying it by the factor 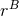 , where
, where 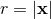 is the spatial radial
distance and
is the spatial radial
distance and 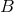 is a complex number,
is a complex number, 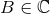 . Let us assume, for definiteness, that
. Let us assume, for definiteness, that 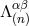 is
composed of multipolar pieces with maximal multipolarity
is
composed of multipolar pieces with maximal multipolarity 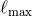 . This means that we start
the iteration from the linearized metric (35*) – (37) in which the multipolar sums are actually
finite.19
The divergences when
. This means that we start
the iteration from the linearized metric (35*) – (37) in which the multipolar sums are actually
finite.19
The divergences when 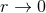 of the source term are typically power-like, say
of the source term are typically power-like, say 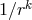 (there are also powers
of the logarithm of
(there are also powers
of the logarithm of  ), and with the previous assumption there will exist a maximal order of divergency,
say
), and with the previous assumption there will exist a maximal order of divergency,
say 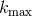 . Thus, when the real part of
. Thus, when the real part of 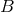 is large enough, i.e.,
is large enough, i.e., 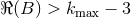 , the “regularized”
source term
, the “regularized”
source term 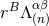 is regular enough when
is regular enough when 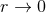 so that one can perfectly apply the retarded integral
operator. This defines the
so that one can perfectly apply the retarded integral
operator. This defines the 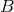 -dependent retarded integral, when
-dependent retarded integral, when 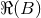 is large enough,
is large enough,
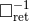 stands for the retarded integral defined by Eq. (31*). It is convenient to introduce
inside the regularizing factor some arbitrary constant length scale
stands for the retarded integral defined by Eq. (31*). It is convenient to introduce
inside the regularizing factor some arbitrary constant length scale 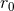 in order to make it dimensionless.
Everywhere in this article we pose
The fate of the constant
in order to make it dimensionless.
Everywhere in this article we pose
The fate of the constant 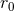 in a detailed calculation will be interesting to follow, as we shall see. Now the
point for our purpose is that the function
in a detailed calculation will be interesting to follow, as we shall see. Now the
point for our purpose is that the function 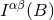 on the complex plane, which was originally
defined only when
on the complex plane, which was originally
defined only when 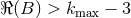 , admits a unique analytic continuation to all values of
, admits a unique analytic continuation to all values of
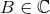 except at some integer values. Furthermore, the analytic continuation of
except at some integer values. Furthermore, the analytic continuation of 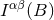 can be
expanded, when
can be
expanded, when 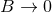 (namely the limit of interest to us) into a Laurent expansion involving
in general some multiple poles. The key idea, as we shall prove, is that the finite part, or the
coefficient of the zeroth power of
(namely the limit of interest to us) into a Laurent expansion involving
in general some multiple poles. The key idea, as we shall prove, is that the finite part, or the
coefficient of the zeroth power of 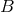 in that expansion, represents the particular solution
we are looking for. We write the Laurent expansion of
in that expansion, represents the particular solution
we are looking for. We write the Laurent expansion of 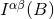 , when
, when  , in the form
where
, in the form
where 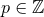 , and the various coefficients
, and the various coefficients 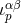 are functions of the field point
are functions of the field point 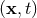 . When
. When 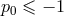 there are poles; and
there are poles; and 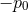 , which depends on
, which depends on 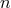 , refers to the maximal order of these poles. By applying
the d’Alembertian operator onto both sides of Eq. (43*), and equating the different powers of
, refers to the maximal order of these poles. By applying
the d’Alembertian operator onto both sides of Eq. (43*), and equating the different powers of 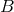 , we arrive
at
, we arrive
at
As we see, the case 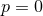 shows that the finite-part coefficient in Eq. (43*), namely
shows that the finite-part coefficient in Eq. (43*), namely 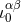 , is a
particular solution of the requested equation:
, is a
particular solution of the requested equation: 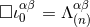 . Furthermore, we can prove that this solution,
by its very construction, owns the same structure made of a multipolar expansion singular at
. Furthermore, we can prove that this solution,
by its very construction, owns the same structure made of a multipolar expansion singular at  as the
corresponding source.
as the
corresponding source.
Let us forget about the intermediate name 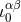 , and denote, from now on, the latter solution by
, and denote, from now on, the latter solution by
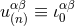 , or, in more explicit terms,
, or, in more explicit terms,
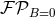 means the previously detailed operations of considering the analytic
continuation, taking the Laurent expansion, and picking up the finite-part coefficient when
means the previously detailed operations of considering the analytic
continuation, taking the Laurent expansion, and picking up the finite-part coefficient when 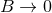 .
The story is not complete, however, because
.
The story is not complete, however, because 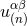 does not fulfill the constraint of harmonic
coordinates (39b); its divergence, say
does not fulfill the constraint of harmonic
coordinates (39b); its divergence, say 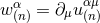 , is different from zero in general. From the fact
that the source term is divergence-free in vacuum,
, is different from zero in general. From the fact
that the source term is divergence-free in vacuum, 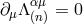 [see Eq. (28*)], we find instead
The factor
[see Eq. (28*)], we find instead
The factor 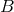 comes from the differentiation of the regularization factor
comes from the differentiation of the regularization factor 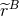 . So,
. So, 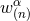 is zero only in
the special case where the Laurent expansion of the retarded integral in Eq. (46*) does not develop any
simple pole when
is zero only in
the special case where the Laurent expansion of the retarded integral in Eq. (46*) does not develop any
simple pole when  . Fortunately, when it does, the structure of the pole is quite easy
to control. We find that it necessarily consists of an homogeneous solution of the source-free
d’Alembertian equation, and, what is more (from its stationarity in the past), that solution is a
retarded one. Hence, taking into account the index structure of
. Fortunately, when it does, the structure of the pole is quite easy
to control. We find that it necessarily consists of an homogeneous solution of the source-free
d’Alembertian equation, and, what is more (from its stationarity in the past), that solution is a
retarded one. Hence, taking into account the index structure of 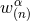 , there must exist four
STF-tensorial functions of
, there must exist four
STF-tensorial functions of 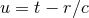 , say
, say 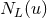 ,
, 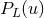 ,
, 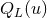 and
and 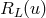 , such that
, such that
From that expression we are able to find a new object, say 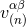 , which takes the same
structure as
, which takes the same
structure as  (a retarded solution of the source-free wave equation) and, furthermore, whose
divergence is exactly the opposite of the divergence of
(a retarded solution of the source-free wave equation) and, furthermore, whose
divergence is exactly the opposite of the divergence of  , i.e.
, i.e. 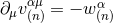 . Such a
. Such a
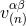 is not unique, but we shall see that it is simply necessary to make a choice for
is not unique, but we shall see that it is simply necessary to make a choice for 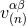 (the simplest one) in order to obtain the general solution. The formulas that we adopt are
(the simplest one) in order to obtain the general solution. The formulas that we adopt are
Notice the presence of anti-derivatives, denoted e.g., by 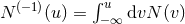 ; there is no problem
with the limit
; there is no problem
with the limit  since all the corresponding functions are zero when
since all the corresponding functions are zero when  . The choice made
in Eqs. (48) is dictated by the fact that the
. The choice made
in Eqs. (48) is dictated by the fact that the 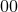 component involves only some monopolar and
dipolar terms, and that the spatial trace
component involves only some monopolar and
dipolar terms, and that the spatial trace 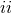 is monopolar:
is monopolar: 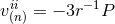 . Finally, if we pose
. Finally, if we pose
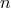 -th post-Minkowskian order. By
induction the same method applies to any order
-th post-Minkowskian order. By
induction the same method applies to any order 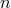 , and, therefore, we have constructed a complete
post-Minkowskian series (38*) based on the linearized approximation
, and, therefore, we have constructed a complete
post-Minkowskian series (38*) based on the linearized approximation 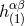 given by Eqs. (35*) – (37). The
previous procedure constitutes an algorithm, which can be (and has recently been [74*, 197*])
implemented by an algebraic computer programme. Again, note that this algorithm permits solving the
full Einstein field equations together with the gauge condition (i.e., not only the relaxed field
equations).
given by Eqs. (35*) – (37). The
previous procedure constitutes an algorithm, which can be (and has recently been [74*, 197*])
implemented by an algebraic computer programme. Again, note that this algorithm permits solving the
full Einstein field equations together with the gauge condition (i.e., not only the relaxed field
equations).
2.4 Generality of the MPM solution
We have a solution, but is that a general solution? The answer, “yes”, is provided by the following result [57*].
Theorem 2. The most general solution of the harmonic-coordinates Einstein field equations in the vacuum region outside an isolated source, admitting some post-Minkowskian and multipolar expansions, is given by the previous construction as
It depends on two sets of arbitrary STF-tensorial functions of time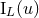 and
and 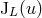 (satisfying the
conservation laws) defined by Eqs. (36), and on four supplementary functions
(satisfying the
conservation laws) defined by Eqs. (36), and on four supplementary functions  parametrizing the gauge vector (37).
parametrizing the gauge vector (37).
The proof is quite easy. With Eq. (49*) we obtained a particular solution of the system of equations (39).
To it we should add the most general solution of the corresponding homogeneous system of equations, which
is obtained by setting 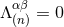 into Eqs. (39). But this homogeneous system of equations is nothing
but the linearized vacuum field equations (33), to which we know the most general solution
into Eqs. (39). But this homogeneous system of equations is nothing
but the linearized vacuum field equations (33), to which we know the most general solution
 given by Eqs. (35*) – (37). Thus, we must add to our particular solution
given by Eqs. (35*) – (37). Thus, we must add to our particular solution 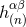 a general
homogeneous solution that is necessarily of the type
a general
homogeneous solution that is necessarily of the type ![αβ h(1)[δIL,...,δZL ]](article456x.gif) , where
, where 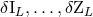 denote
some corrections to the multipole moments at the
denote
some corrections to the multipole moments at the 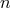 -th post-Minkowskian order (with the
monopole
-th post-Minkowskian order (with the
monopole 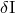 and dipoles
and dipoles 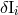 ,
, 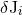 being constant). It is then clear, since precisely the
linearized metric is a linear functional of all these moments, that the previous corrections to
the moments can be absorbed into a re-definition of the original ones
being constant). It is then clear, since precisely the
linearized metric is a linear functional of all these moments, that the previous corrections to
the moments can be absorbed into a re-definition of the original ones 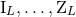 by posing
by posing
After re-arranging the metric in terms of these new moments, taking into account the fact that the
precision of the metric is limited to the 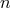 -th post-Minkowskian order, and dropping the superscript
“new”, we find exactly the same solution as the one we had before (indeed, the moments are arbitrary
functions of time) – hence the proof.
-th post-Minkowskian order, and dropping the superscript
“new”, we find exactly the same solution as the one we had before (indeed, the moments are arbitrary
functions of time) – hence the proof.
The six sets of multipole moments 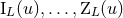 contain the physical information about any
isolated source as seen in its exterior. However, as we now discuss, it is always possible to find two, and only
two, sets of multipole moments,
contain the physical information about any
isolated source as seen in its exterior. However, as we now discuss, it is always possible to find two, and only
two, sets of multipole moments, 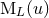 and
and 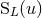 , for parametrizing the most general isolated source as
well. The route for constructing such a general solution is to get rid of the moments
, for parametrizing the most general isolated source as
well. The route for constructing such a general solution is to get rid of the moments 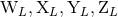 at
the linearized level by performing the linearized gauge transformation
at
the linearized level by performing the linearized gauge transformation 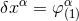 , where
, where 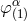 is
the gauge vector given by Eqs. (37). So, at the linearized level, we have only the two types
of moments
is
the gauge vector given by Eqs. (37). So, at the linearized level, we have only the two types
of moments 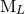 and
and 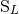 , parametrizing
, parametrizing 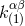 by the same formulas as in Eqs. (36). We
must be careful to denote these moments with names different from
by the same formulas as in Eqs. (36). We
must be careful to denote these moments with names different from 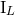 and
and 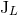 because
they will ultimately correspond to a different physical source. Then we apply exactly the same
post-Minkowskian algorithm, following the formulas (45*) – (49*) as we did above, but starting from the
gauge-transformed linear metric
because
they will ultimately correspond to a different physical source. Then we apply exactly the same
post-Minkowskian algorithm, following the formulas (45*) – (49*) as we did above, but starting from the
gauge-transformed linear metric  instead of
instead of 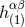 . The result of the iteration is therefore some
. The result of the iteration is therefore some
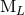 and
and
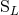 are related to the source moments
are related to the source moments 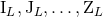 by some (quite involved) non-linear
equations. We shall give in Eqs. (97) – (98) the most up to date relations we have between these
moments. Therefore, the most general solution of the field equations, modulo a coordinate
transformation, can be obtained by starting from the linearized metric
by some (quite involved) non-linear
equations. We shall give in Eqs. (97) – (98) the most up to date relations we have between these
moments. Therefore, the most general solution of the field equations, modulo a coordinate
transformation, can be obtained by starting from the linearized metric ![kα(β1)[ML, SL ]](article482x.gif) instead of the more
complicated
instead of the more
complicated ![αβ α β β α αβ μ k(1)[IL,JL] + ∂ φ(1) + ∂ φ(1) − η ∂ μφ(1)](article483x.gif) , and continuing the post-Minkowskian
calculation.
, and continuing the post-Minkowskian
calculation.
So why not consider from the start that the best description of the isolated source is provided by only
the two types of multipole moments, 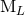 and
and 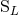 , instead of the six types,
, instead of the six types, 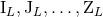 ? The reason
is that we shall determine in Theorem 6 below the explicit closed-form expressions of the six source
moments
? The reason
is that we shall determine in Theorem 6 below the explicit closed-form expressions of the six source
moments 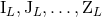 , but that, by contrast, it seems to be impossible to obtain some similar
closed-form expressions for the canonical moments
, but that, by contrast, it seems to be impossible to obtain some similar
closed-form expressions for the canonical moments 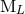 and
and 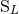 . The only thing we can do is to write
down the explicit non-linear algorithm that computes
. The only thing we can do is to write
down the explicit non-linear algorithm that computes 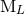 ,
, 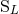 starting from
starting from 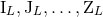 . In
consequence, it is better to view the moments
. In
consequence, it is better to view the moments  as more “fundamental” than
as more “fundamental” than 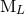 and
and 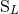 ,
in the sense that they appear to be more tightly related to the description of the source, since they admit
closed-form expressions as some explicit integrals over the source. Hence, we choose to refer collectively to
the six moments
,
in the sense that they appear to be more tightly related to the description of the source, since they admit
closed-form expressions as some explicit integrals over the source. Hence, we choose to refer collectively to
the six moments 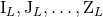 as the multipole moments of the source. This being said, the moments
as the multipole moments of the source. This being said, the moments
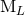 and
and 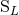 are generally very useful in practical computations because they yield a simpler
post-Minkowskian iteration. Then, one can generally come back to the more fundamental source-rooted
moments by using the fact that
are generally very useful in practical computations because they yield a simpler
post-Minkowskian iteration. Then, one can generally come back to the more fundamental source-rooted
moments by using the fact that 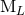 and
and 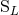 differ from the corresponding
differ from the corresponding 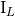 and
and  only
by high-order post-Newtonian terms like 2.5PN; see Eqs. (97) – (98) below. Indeed, this is to
be expected because the physical difference between both types of moments stems only from
non-linearities.
only
by high-order post-Newtonian terms like 2.5PN; see Eqs. (97) – (98) below. Indeed, this is to
be expected because the physical difference between both types of moments stems only from
non-linearities.
2.5 Near-zone and far-zone structures
In our presentation of the post-Minkowskian algorithm (45*) – (49*) we have for the moment omitted a
crucial recursive hypothesis, which is required in order to prove that at each post-Minkowskian order
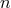 , the inverse d’Alembertian operator can be applied in the way we did – notably that the
, the inverse d’Alembertian operator can be applied in the way we did – notably that the
 -dependent retarded integral can be analytically continued down to a neighbourhood of
-dependent retarded integral can be analytically continued down to a neighbourhood of
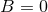 . This hypothesis is that the “near-zone” expansion, i.e., when
. This hypothesis is that the “near-zone” expansion, i.e., when 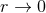 , of each one of the
post-Minkowskian coefficients
, of each one of the
post-Minkowskian coefficients 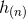 has a certain structure (here we often omit the space-time
indices
has a certain structure (here we often omit the space-time
indices  ); this hypothesis is established as a theorem once the mathematical induction
succeeds.
); this hypothesis is established as a theorem once the mathematical induction
succeeds.
Theorem 3. The general structure of the expansion of the post-Minkowskian exterior metric in the
near-zone (when 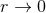 ) is of the type:
) is of the type: 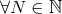 ,
,
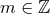 , with
, with 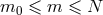 (and
(and 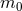 becoming more and more negative as
becoming more and more negative as 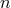 grows),
grows), 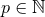 with
with 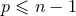 . The functions
. The functions 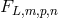 are multilinear functionals of the source multipole moments
are multilinear functionals of the source multipole moments
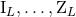 .
.
For the proof see Ref. [57*]. As we see, the near-zone expansion involves, besides the simple powers of  ,
some powers of the logarithm of
,
some powers of the logarithm of  , with a maximal power of
, with a maximal power of  . As a corollary of that theorem, we
find, by restoring all the powers of
. As a corollary of that theorem, we
find, by restoring all the powers of  in Eq. (53*) and using the fact that each
in Eq. (53*) and using the fact that each  goes into the
combination
goes into the
combination 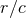 , that the general structure of the post-Newtonian expansion (
, that the general structure of the post-Newtonian expansion ( ) is necessarily
of the type
) is necessarily
of the type
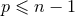 (and
(and 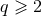 ). The post-Newtonian expansion proceeds not only with the normal powers
of
). The post-Newtonian expansion proceeds not only with the normal powers
of 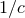 but also with powers of the logarithm of
but also with powers of the logarithm of  [57]. It is remarkable that there is no more
complicated structure like for instance
[57]. It is remarkable that there is no more
complicated structure like for instance 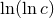 .
.
Paralleling the structure of the near-zone expansion, we have a similar result concerning the
structure of the far-zone expansion at Minkowskian future null infinity, i.e., when 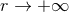 with
with
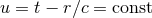 :
:  ,
,
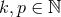 , with
, with 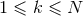 , and where, likewise in the near-zone expansion (53*), some powers of
logarithms, such that
, and where, likewise in the near-zone expansion (53*), some powers of
logarithms, such that 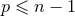 , appear. The appearance of logarithms in the far-zone expansion of the
harmonic-coordinates metric has been known since the work of Fock [202*]. One knows also that
this is a coordinate effect, because the study of the “asymptotic” structure of space-time at
future null infinity by Bondi et al. [93*], Sachs [368*], and Penrose [337*, 338*], has revealed
the existence of other coordinate systems that avoid the appearance of any logarithms: the
so-called radiative coordinates, in which the far-zone expansion of the metric proceeds with simple
powers of the inverse radial distance. Hence, the logarithms are simply an artifact of the use of
harmonic coordinates [252, 304*, 41*]. The following theorem, proved in Ref. [41*], shows that our
general construction of the metric in the exterior of the source, when developed at future null
infinity, is consistent with the Bondi–Sachs–Penrose [93*, 368, 337*, 338*] approach to gravitational
radiation.
, appear. The appearance of logarithms in the far-zone expansion of the
harmonic-coordinates metric has been known since the work of Fock [202*]. One knows also that
this is a coordinate effect, because the study of the “asymptotic” structure of space-time at
future null infinity by Bondi et al. [93*], Sachs [368*], and Penrose [337*, 338*], has revealed
the existence of other coordinate systems that avoid the appearance of any logarithms: the
so-called radiative coordinates, in which the far-zone expansion of the metric proceeds with simple
powers of the inverse radial distance. Hence, the logarithms are simply an artifact of the use of
harmonic coordinates [252, 304*, 41*]. The following theorem, proved in Ref. [41*], shows that our
general construction of the metric in the exterior of the source, when developed at future null
infinity, is consistent with the Bondi–Sachs–Penrose [93*, 368, 337*, 338*] approach to gravitational
radiation.
Theorem 4. The most general multipolar-post-Minkowskian solution, stationary in the past [see Eq. (29*)],
admits some radiative coordinates 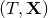 , for which the expansion at future null infinity,
, for which the expansion at future null infinity, 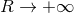 with
with
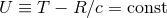 , takes the form
, takes the form
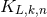 are computable functionals of the source multipole moments. In radiative coordinates
the retarded time
are computable functionals of the source multipole moments. In radiative coordinates
the retarded time 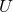 is a null coordinate in the asymptotic limit. The metric
is a null coordinate in the asymptotic limit. The metric 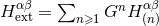 is
asymptotically simple in the sense of Penrose [337, 338, 220*], perturbatively to any post-Minkowskian
order.
is
asymptotically simple in the sense of Penrose [337, 338, 220*], perturbatively to any post-Minkowskian
order.
Proof. We introduce a linearized “radiative” metric by performing a gauge transformation of the harmonic-coordinates metric defined by Eqs. (35*) – (37), namely
where the gauge vector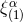 is
This gauge transformation is non-harmonic:
Its effect is to correct for the well-known logarithmic deviation of the retarded time in harmonic
coordinates, with respect to the true space-time characteristic or light cones. After the change
of gauge, the coordinate
is
This gauge transformation is non-harmonic:
Its effect is to correct for the well-known logarithmic deviation of the retarded time in harmonic
coordinates, with respect to the true space-time characteristic or light cones. After the change
of gauge, the coordinate 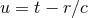 coincides with a null coordinate at the linearized
level.21
This is the requirement to be satisfied by a linearized metric so that it can constitute the linearized
approximation to a full (post-Minkowskian) radiative field [304]. One can easily show that, at the dominant
order when
coincides with a null coordinate at the linearized
level.21
This is the requirement to be satisfied by a linearized metric so that it can constitute the linearized
approximation to a full (post-Minkowskian) radiative field [304]. One can easily show that, at the dominant
order when 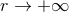 ,
where
,
where 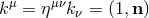 is the outgoing Minkowskian null vector. Given any
is the outgoing Minkowskian null vector. Given any 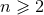 , let us recursively
assume that we have obtained all the previous radiative post-Minkowskian coefficients
, let us recursively
assume that we have obtained all the previous radiative post-Minkowskian coefficients  , i.e.
, i.e.
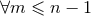 , and that all of them satisfy
From this induction hypothesis one can prove that the
, and that all of them satisfy
From this induction hypothesis one can prove that the 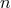 -th post-Minkowskian source term
-th post-Minkowskian source term
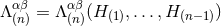 is such that
To the leading order this term takes the classic form of the stress-energy tensor of massless particles, with
is such that
To the leading order this term takes the classic form of the stress-energy tensor of massless particles, with
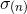 being proportional to the power in the massless waves. One can show that all the problems with the
appearance of logarithms come from the retarded integral of the terms in Eq. (62*) that behave like
being proportional to the power in the massless waves. One can show that all the problems with the
appearance of logarithms come from the retarded integral of the terms in Eq. (62*) that behave like
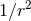 : See indeed the integration formula (83*), which behaves like
: See indeed the integration formula (83*), which behaves like 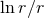 at infinity. But
now, thanks to the particular index structure of the term (62*), we can correct for the effect
by adjusting the gauge at the
at infinity. But
now, thanks to the particular index structure of the term (62*), we can correct for the effect
by adjusting the gauge at the 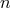 -th post-Minkowskian order. We pose, as a gauge vector,
where
-th post-Minkowskian order. We pose, as a gauge vector,
where 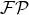 refers to the same finite part operation as in Eq. (45*). This vector is such that the logarithms
that will appear in the corresponding gauge terms cancel out the logarithms coming from the retarded
integral of the source term (62*); see Ref. [41*] for the details. Hence, to the
refers to the same finite part operation as in Eq. (45*). This vector is such that the logarithms
that will appear in the corresponding gauge terms cancel out the logarithms coming from the retarded
integral of the source term (62*); see Ref. [41*] for the details. Hence, to the 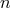 -th post-Minkowskian order,
we define the radiative metric as
Here
-th post-Minkowskian order,
we define the radiative metric as
Here 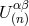 and
and 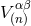 denote the quantities that are the analogues of
denote the quantities that are the analogues of 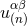 and
and 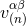 , which
were introduced into the harmonic-coordinates algorithm: See Eqs. (45*) – (48). In particular,
these quantities are constructed in such a way that the sum
, which
were introduced into the harmonic-coordinates algorithm: See Eqs. (45*) – (48). In particular,
these quantities are constructed in such a way that the sum 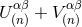 is divergence-free,
so we see that the radiative metric does not obey the harmonic-gauge condition, but instead
The far-zone expansion of the latter metric is of the type (56*), i.e., is free of any logarithms, and the
retarded time in these coordinates tends asymptotically toward a null coordinate at future null infinity. The
property of asymptotic simplicity, in the form given by Geroch & Horowitz [220], is proved by introducing
the usual conformal factor
is divergence-free,
so we see that the radiative metric does not obey the harmonic-gauge condition, but instead
The far-zone expansion of the latter metric is of the type (56*), i.e., is free of any logarithms, and the
retarded time in these coordinates tends asymptotically toward a null coordinate at future null infinity. The
property of asymptotic simplicity, in the form given by Geroch & Horowitz [220], is proved by introducing
the usual conformal factor 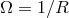 in radiative coordinates [41]. Finally, it can be checked that the
metric so constructed, which is a functional of the source multipole moments
in radiative coordinates [41]. Finally, it can be checked that the
metric so constructed, which is a functional of the source multipole moments 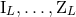 (from the
definition of the algorithm), is as general as the general harmonic-coordinate metric of Theorem 2, since it
merely differs from it by a coordinate transformation
(from the
definition of the algorithm), is as general as the general harmonic-coordinate metric of Theorem 2, since it
merely differs from it by a coordinate transformation 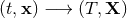 , where
, where 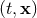 are the
harmonic coordinates and
are the
harmonic coordinates and 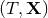 the radiative ones, together with a re-definition of the multipole
moments.
the radiative ones, together with a re-definition of the multipole
moments.

![c3 ∫ √--- [ ] IEH = ------ d4x − gR + Imat Ψ,gα β . (17 ) 16 πG](article164x.gif)
![αβ 2 8πG αβ E [g,∂g,∂ g] = -c4-T [Ψ, g], (18 )](article165x.gif)
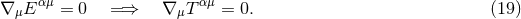




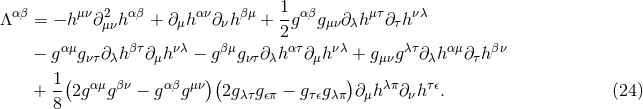
![Λ αβ = N αβ[h,h ] + M αβ[h,h, h] + L αβ[h,h,h,h ] + 𝒪 (h5). (25 )](article202x.gif)
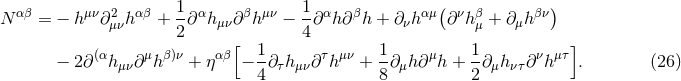


![∂--[ αβ ] ∂t h (x,t) = 0 when t ≤ − 𝒯 . (29)](article225x.gif)

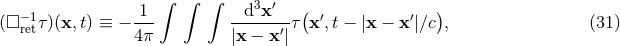



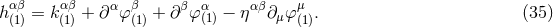
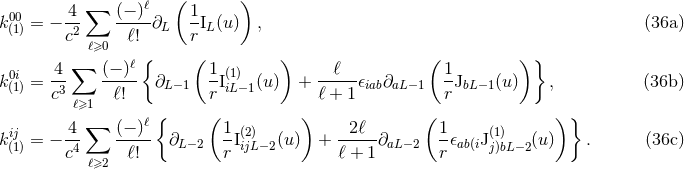
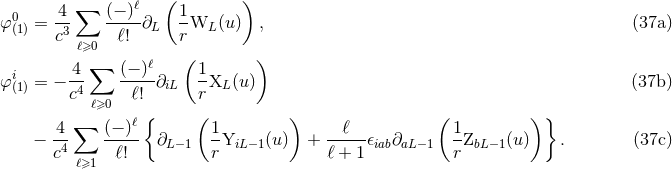

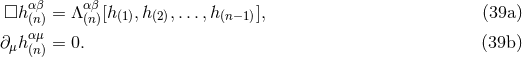
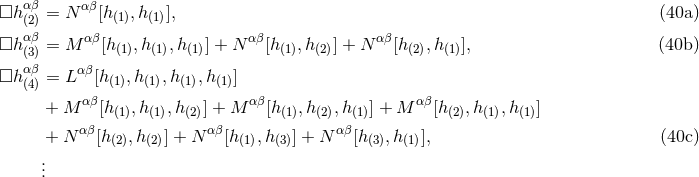
![[ ] Iαβ(B ) ≡ □ −1 ^rB Λαβ , (41 ) ret (n)](article386x.gif)


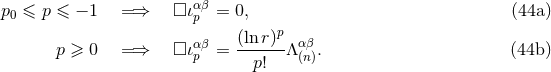
![[ ] uαβ = ℱ 𝒫B=0 □ −1 ^rB Λαβ , (45 ) (n) ret (n)](article414x.gif)
![[ ] w α = ℱ 𝒫 □ −1 B ^rB niΛ αi . (46 ) (n) B=0 ret r (n)](article420x.gif)
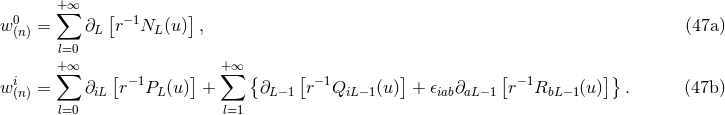
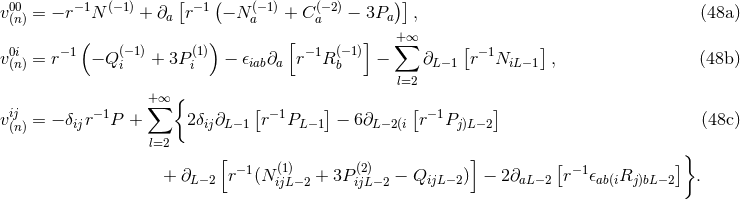

![αβ +∑∞ n αβ h ext = G h (n)[IL, JL,...,ZL ]. (50 ) n=1](article449x.gif)

![αβ +∑∞ n αβ k ext = G k (n)[ML, SL]. (52 ) n=1](article478x.gif)
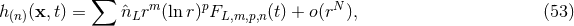

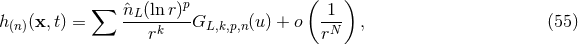
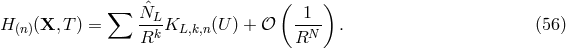
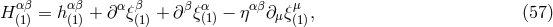




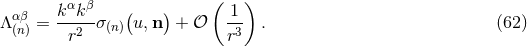
![[ ∫ ] α −1 kα-- u ξ(n) = ℱ 𝒫 □ ret 2r2 dvσ (n)(v,n ) , (63 ) −∞](article574x.gif)