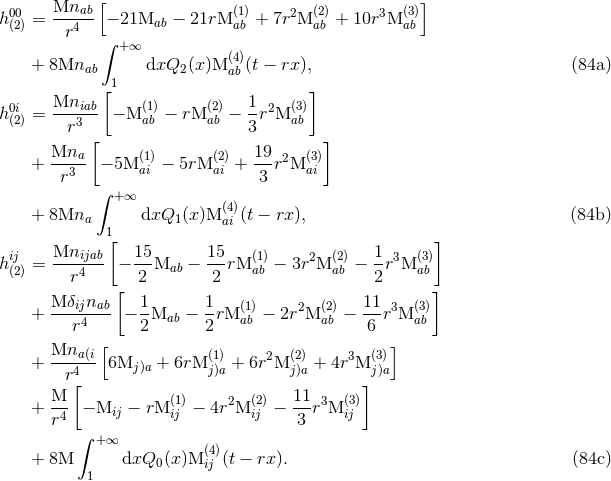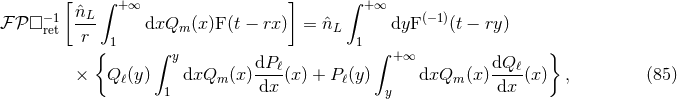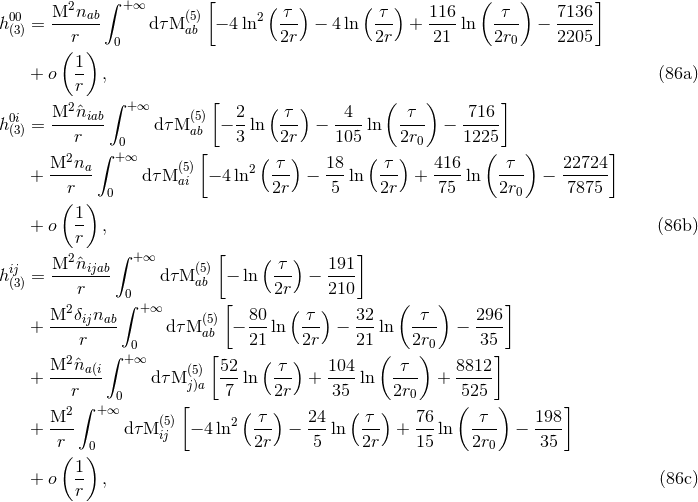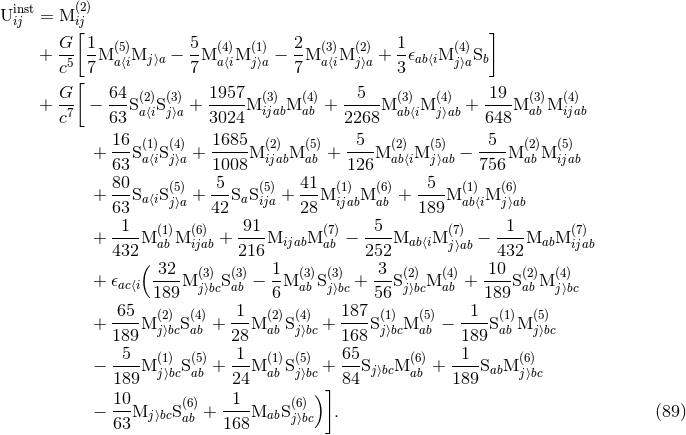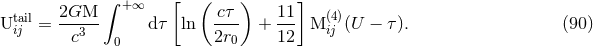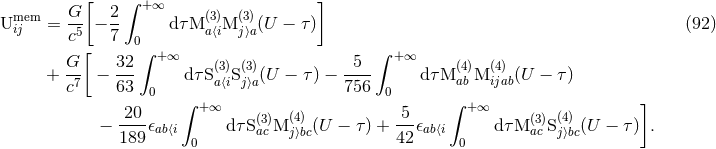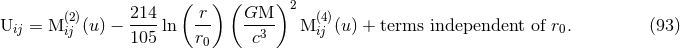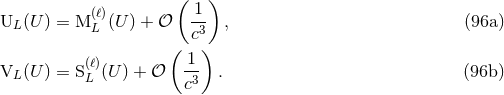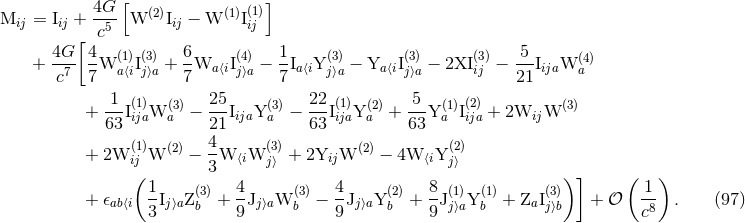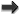3 Asymptotic Gravitational Waveform
3.1 The radiative multipole moments
The leading-order term 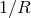 of the metric in radiative coordinates
of the metric in radiative coordinates 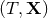 as given in Theorem 4,
neglecting
as given in Theorem 4,
neglecting 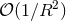 , yields the operational definition of two sets of STF radiative multipole moments,
mass-type
, yields the operational definition of two sets of STF radiative multipole moments,
mass-type 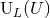 and current-type
and current-type 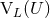 . As we have seen, radiative coordinates are such that the
retarded time
. As we have seen, radiative coordinates are such that the
retarded time 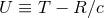 becomes asymptotically a null coordinate at future null infinity. The radiative
moments are defined from the spatial components
becomes asymptotically a null coordinate at future null infinity. The radiative
moments are defined from the spatial components 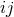 of the metric in a transverse-traceless (TT) radiative
coordinate system. By definition, we have [403*]
of the metric in a transverse-traceless (TT) radiative
coordinate system. By definition, we have [403*]
We have formally re-summed the whole post-Minkowskian series in Eq. (56*) from 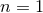 up to
up to 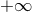 .
As before we denote for instance
.
As before we denote for instance 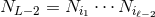 and so on, where
and so on, where 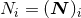 and
and 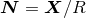 .
The TT algebraic projection operator
.
The TT algebraic projection operator 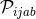 has already been defined at the occasion of the
quadrupole-moment formalism in Eq. (2*); and obviously the multipole decomposition (66) represents the
generalization of the quadrupole formalism. Notice that the meaning of Eq. (66) is for the
moment rather empty, because we do not yet know how to relate the radiative moments to
the actual source parameters. Only at the Newtonian level do we know this relation, which is
has already been defined at the occasion of the
quadrupole-moment formalism in Eq. (2*); and obviously the multipole decomposition (66) represents the
generalization of the quadrupole formalism. Notice that the meaning of Eq. (66) is for the
moment rather empty, because we do not yet know how to relate the radiative moments to
the actual source parameters. Only at the Newtonian level do we know this relation, which is
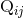 is the Newtonian quadrupole moment (3*). Associated to the asymptotic waveform (66) we can
compute by standard methods the total energy flux
is the Newtonian quadrupole moment (3*). Associated to the asymptotic waveform (66) we can
compute by standard methods the total energy flux 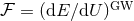 and angular momentum flux
and angular momentum flux
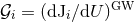 in gravitational waves [403*]:
in gravitational waves [403*]:
Next we introduce two unit polarization vectors 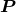 and
and 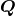 , orthogonal and transverse to the
direction of propagation
, orthogonal and transverse to the
direction of propagation 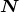 (hence
(hence 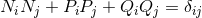 ). Our convention for the choice of
). Our convention for the choice of 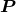 and
and 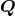 will be clarified in Section 9.4. Then the two “plus” and “cross” polarization states of the
asymptotic waveform are defined by
will be clarified in Section 9.4. Then the two “plus” and “cross” polarization states of the
asymptotic waveform are defined by
Although the multipole decomposition (66) is completely general, it will also be important, having
in view the comparison between the post-Newtonian and numerical results (see for instance
Refs. [107*, 34, 237, 97, 98*]), to consider separately the various modes 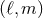 of the asymptotic
waveform as defined with respect to a basis of spin-weighted spherical harmonics of weight
of the asymptotic
waveform as defined with respect to a basis of spin-weighted spherical harmonics of weight 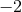 . Those
harmonics are function of the spherical angles
. Those
harmonics are function of the spherical angles 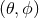 defining the direction of propagation
defining the direction of propagation 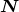 , and given
by
, and given
by
where 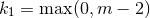 and
and  . We thus decompose
. We thus decompose 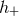 and
and 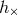 onto the basis of such spin-weighted spherical harmonics, which means (see e.g., [107, 272*])
onto the basis of such spin-weighted spherical harmonics, which means (see e.g., [107, 272*])
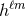 from a surface integral,
where the overline refers to the complex conjugation. On the other hand, we can also relate
from a surface integral,
where the overline refers to the complex conjugation. On the other hand, we can also relate 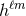 to the
radiative multipole moments
to the
radiative multipole moments 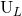 and
and 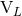 . The result is
where
. The result is
where 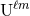 and
and 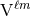 denote the radiative mass and current moments in standard (non-STF) guise.
These are related to the STF moments by
denote the radiative mass and current moments in standard (non-STF) guise.
These are related to the STF moments by
Here 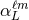 denotes the STF tensor connecting together the usual basis of spherical harmonics
denotes the STF tensor connecting together the usual basis of spherical harmonics 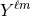 to the
set of STF tensors
to the
set of STF tensors 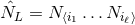 (where the brackets indicate the STF projection). Indeed both
(where the brackets indicate the STF projection). Indeed both 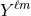 and
and 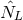 are basis of an irreducible representation of weight
are basis of an irreducible representation of weight 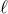 of the rotation group; the two basis are related
by22
of the rotation group; the two basis are related
by22
In Section 9.5 we shall present all the modes 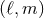 of gravitational waves from inspiralling compact
binaries up to 3PN order, and even 3.5PN order for the dominant mode
of gravitational waves from inspiralling compact
binaries up to 3PN order, and even 3.5PN order for the dominant mode 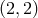 .
.
3.2 Gravitational-wave tails and tails-of-tails
We learned from Theorem 4 the general method which permits the computation of the radiative multipole
moments 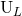 ,
, 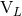 in terms of the source moments
in terms of the source moments 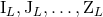 , or in terms of the intermediate
canonical moments
, or in terms of the intermediate
canonical moments 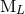 ,
, 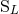 discussed in Section 2.4. We shall now show that the relation
between
discussed in Section 2.4. We shall now show that the relation
between 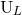 ,
, 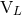 and
and 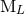 ,
, 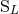 (say) includes tail effects starting at the relative 1.5PN
order.
(say) includes tail effects starting at the relative 1.5PN
order.
Tails are due to the back-scattering of multipolar waves off the Schwarzschild curvature generated by
the total mass monopole 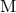 of the source. They correspond to the non-linear interaction
between
of the source. They correspond to the non-linear interaction
between 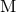 and the multipole moments
and the multipole moments 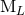 and
and  , and are given by some non-local
integrals, extending over the past history of the source. At the 1.5PN order we find [59*, 44*]
, and are given by some non-local
integrals, extending over the past history of the source. At the 1.5PN order we find [59*, 44*]
where 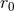 is the length scale introduced in Eq. (42*), and the constants
is the length scale introduced in Eq. (42*), and the constants 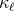 and
and 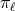 are given by
are given by
Recall from the gauge vector 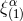 found in Eq. (58*) that the retarded time
found in Eq. (58*) that the retarded time 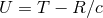 in
radiative coordinates is related to the retarded time
in
radiative coordinates is related to the retarded time 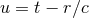 in harmonic coordinates by
in harmonic coordinates by
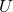 as given by Eq. (78*) into Eqs. (76) we obtain the radiative moments expressed in terms of
“source-rooted” harmonic coordinates
as given by Eq. (78*) into Eqs. (76) we obtain the radiative moments expressed in terms of
“source-rooted” harmonic coordinates 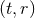 , e.g.,
The remainder
, e.g.,
The remainder 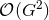 in Eq. (78*) is negligible here. This expression no longer depends on the constant
in Eq. (78*) is negligible here. This expression no longer depends on the constant
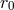 , i.e., we find that
, i.e., we find that 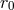 gets replaced by
gets replaced by  . If we now replace the harmonic coordinates
. If we now replace the harmonic coordinates 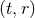 to
some new ones, such as, for instance, some “Schwarzschild-like” coordinates
to
some new ones, such as, for instance, some “Schwarzschild-like” coordinates 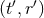 such that
such that 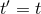 and
and
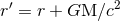 (and
(and 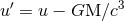 ), we get
where
), we get
where 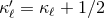 . This shows that the constant
. This shows that the constant  (and
(and 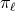 as well) depends on the choice of
source-rooted coordinates
as well) depends on the choice of
source-rooted coordinates  : For instance, we have
: For instance, we have 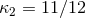 in harmonic coordinates from
Eq. (77a), but
in harmonic coordinates from
Eq. (77a), but 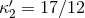 in Schwarzschild coordinates [345].
in Schwarzschild coordinates [345].
The tail integrals in Eqs. (76) involve all the instants from 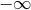 in the past up to the
current retarded time
in the past up to the
current retarded time 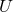 . However, strictly speaking, they do not extend up to infinite past,
since we have assumed in Eq. (29*) that the metric is stationary before the date
. However, strictly speaking, they do not extend up to infinite past,
since we have assumed in Eq. (29*) that the metric is stationary before the date 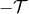 . The
range of integration of the tails is therefore limited a priori to the time interval
. The
range of integration of the tails is therefore limited a priori to the time interval ![[− 𝒯 ,U ]](article690x.gif) .
But now, once we have derived the tail integrals, thanks to the latter technical assumption of
stationarity in the past, we can argue that the results are in fact valid in more general situations for
which the field has never been stationary. We have in mind the case of two bodies moving
initially on some unbound (hyperbolic-like) orbit, and which capture each other, because of the
loss of energy by gravitational radiation, to form a gravitationally bound system around time
.
But now, once we have derived the tail integrals, thanks to the latter technical assumption of
stationarity in the past, we can argue that the results are in fact valid in more general situations for
which the field has never been stationary. We have in mind the case of two bodies moving
initially on some unbound (hyperbolic-like) orbit, and which capture each other, because of the
loss of energy by gravitational radiation, to form a gravitationally bound system around time
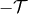 .
.
In this situation let us check, using a simple Newtonian model for the behaviour of the
multipole moment 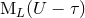 when
when 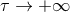 , that the tail integrals, when assumed to
extend over the whole time interval
, that the tail integrals, when assumed to
extend over the whole time interval ![[− ∞, U ]](article694x.gif) , remain perfectly well-defined (i.e., convergent) at
the integration bound
, remain perfectly well-defined (i.e., convergent) at
the integration bound 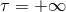 . Indeed it can be shown [180] that the motion of initially
free particles interacting gravitationally is given by
. Indeed it can be shown [180] that the motion of initially
free particles interacting gravitationally is given by 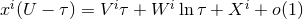 ,
where
,
where 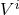 ,
,  and
and  denote constant vectors, and
denote constant vectors, and 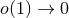 when
when 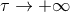 . From
that physical assumption we find that the multipole moments behave when
. From
that physical assumption we find that the multipole moments behave when  like
like
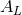 ,
, 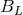 and
and 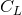 are constant tensors. We used the fact that the moment
are constant tensors. We used the fact that the moment 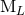 will agree at the
Newtonian level with the standard expression for the
will agree at the
Newtonian level with the standard expression for the 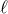 -th mass multipole moment
-th mass multipole moment 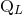 . The
appropriate time derivatives of the moment appearing in Eq. (76a) are therefore dominantly like
which ensures that the tail integral is convergent. This fact can be regarded as an a posteriori
justification of our a priori too restrictive assumption of stationarity in the past. Thus, this
assumption does not seem to yield any physical restriction on the applicability of the final
formulas. However, once again, we emphasize that the past-stationarity is appropriate for real
astrophysical sources of gravitational waves which have been formed at a finite instant in the
past.
. The
appropriate time derivatives of the moment appearing in Eq. (76a) are therefore dominantly like
which ensures that the tail integral is convergent. This fact can be regarded as an a posteriori
justification of our a priori too restrictive assumption of stationarity in the past. Thus, this
assumption does not seem to yield any physical restriction on the applicability of the final
formulas. However, once again, we emphasize that the past-stationarity is appropriate for real
astrophysical sources of gravitational waves which have been formed at a finite instant in the
past.
To obtain the results (76), we must implement in details the post-Minkowskian algorithm presented in
Section 2.3. Let us flash here some results obtained with such algorithm. Consider first the case of the
interaction between the constant mass monopole moment  (or ADM mass) and the time-varying
quadrupole moment
(or ADM mass) and the time-varying
quadrupole moment 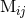 . This coupling will represent the dominant non-static multipole interaction in
the waveform. For these moments we can write the linearized metric using Eq. (35*) in which by definition
of the “canonical” construction we insert the canonical moments
. This coupling will represent the dominant non-static multipole interaction in
the waveform. For these moments we can write the linearized metric using Eq. (35*) in which by definition
of the “canonical” construction we insert the canonical moments 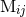 in place of
in place of 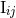 (notice that
(notice that
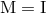 ). We must plug this linearized metric into the quadratic-order part
). We must plug this linearized metric into the quadratic-order part 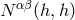 of the gravitational
source term (24) – (25*) and explicitly given by Eq. (26). This yields many terms; to integrate
these following the algorithm [cf. Eq. (45*)], we need some explicit formulas for the retarded
integral of an extended (non-compact-support) source having some definite multipolarity
of the gravitational
source term (24) – (25*) and explicitly given by Eq. (26). This yields many terms; to integrate
these following the algorithm [cf. Eq. (45*)], we need some explicit formulas for the retarded
integral of an extended (non-compact-support) source having some definite multipolarity 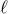 . A
thorough account of the technical formulas necessary for handling the quadratic and cubic
interactions is given in the Appendices of Refs. [50*] and [48*]. For the present computation the most
crucial formula, needed to control the tails, corresponds to a source term behaving like
. A
thorough account of the technical formulas necessary for handling the quadratic and cubic
interactions is given in the Appendices of Refs. [50*] and [48*]. For the present computation the most
crucial formula, needed to control the tails, corresponds to a source term behaving like 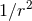 :
:
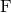 is any smooth function representing a time derivative of the
quadrupole moment, and
is any smooth function representing a time derivative of the
quadrupole moment, and 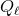 denotes the Legendre function of the second
kind.23
Note that there is no need to include a finite part operation
denotes the Legendre function of the second
kind.23
Note that there is no need to include a finite part operation 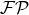 in Eq. (83*) as the integral is convergent.
With the help of this and other formulas we obtain successively the objects defined in this algorithm by
Eqs. (45*) – (48) and finally obtain the quadratic metric (49*) for that multipole interaction. The result
is [60*]24
in Eq. (83*) as the integral is convergent.
With the help of this and other formulas we obtain successively the objects defined in this algorithm by
Eqs. (45*) – (48) and finally obtain the quadratic metric (49*) for that multipole interaction. The result
is [60*]24
The metric is composed of two types of terms: “instantaneous” ones depending on the values of the
quadrupole moment at the retarded time 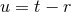 , and “hereditary” tail integrals, depending on all
previous instants
, and “hereditary” tail integrals, depending on all
previous instants 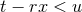 .
.
Let us investigate now the cubic interaction between two mass monopoles 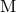 with the mass
quadrupole
with the mass
quadrupole 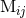 . Obviously, the source term corresponding to this interaction will involve
[see Eq. (40b)] cubic products of three linear metrics, say
. Obviously, the source term corresponding to this interaction will involve
[see Eq. (40b)] cubic products of three linear metrics, say 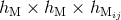 , and quadratic
products between one linear metric and one quadratic, say
, and quadratic
products between one linear metric and one quadratic, say 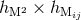 and
and  .
The latter case is the most tricky because the tails present in
.
The latter case is the most tricky because the tails present in 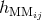 , which are given
explicitly by Eqs. (84), will produce in turn some tails of tails in the cubic metric
, which are given
explicitly by Eqs. (84), will produce in turn some tails of tails in the cubic metric 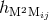 .
The computation is rather involved [48*] but can now be performed by an algebraic computer
programme [74*, 197*]. Let us just mention the most difficult of the needed integration formulas for this
calculation:25
.
The computation is rather involved [48*] but can now be performed by an algebraic computer
programme [74*, 197*]. Let us just mention the most difficult of the needed integration formulas for this
calculation:25
where 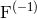 is the time anti-derivative of
is the time anti-derivative of 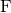 . With this formula and others given in Ref. [48*] we are
able to obtain the closed algebraic form of the cubic metric for the multipole interaction
. With this formula and others given in Ref. [48*] we are
able to obtain the closed algebraic form of the cubic metric for the multipole interaction 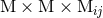 ,
at the leading order when the distance to the source
,
at the leading order when the distance to the source 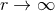 with
with 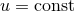 . The result
is26
. The result
is26
where all the moments 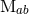 are evaluated at the instant
are evaluated at the instant 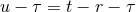 . Notice that the
logarithms in Eqs. (86) contain either the ratio
. Notice that the
logarithms in Eqs. (86) contain either the ratio 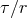 or
or 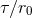 . We shall discuss in Eqs. (93*) – (94*) below
the interesting fate of the arbitrary constant
. We shall discuss in Eqs. (93*) – (94*) below
the interesting fate of the arbitrary constant 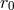 .
.
From Theorem 4, the presence of logarithms of  in Eqs. (86) is an artifact of the harmonic
coordinates
in Eqs. (86) is an artifact of the harmonic
coordinates 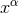 , and it is convenient to gauge them away by introducing radiative coordinates
, and it is convenient to gauge them away by introducing radiative coordinates 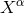 at
future null infinity. For controling the leading
at
future null infinity. For controling the leading 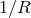 term at infinity, it is sufficient to take into account the
linearized logarithmic deviation of the light cones in harmonic coordinates:
term at infinity, it is sufficient to take into account the
linearized logarithmic deviation of the light cones in harmonic coordinates: 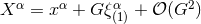 ,
where
,
where  is the gauge vector defined by Eq. (58*) [see also Eq. (78*)]. With this coordinate change one
removes the logarithms of
is the gauge vector defined by Eq. (58*) [see also Eq. (78*)]. With this coordinate change one
removes the logarithms of  in Eqs. (86) and we obtain the radiative (or Bondi-type [93])
logarithmic-free expansion
in Eqs. (86) and we obtain the radiative (or Bondi-type [93])
logarithmic-free expansion
where the moments are evaluated at time 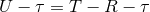 . It is trivial to compute the contribution
of the radiative moments corresponding to that metric. We find the “tail of tail” term which will be
reported in Eq. (91) below.
. It is trivial to compute the contribution
of the radiative moments corresponding to that metric. We find the “tail of tail” term which will be
reported in Eq. (91) below.
3.3 Radiative versus source moments
We first give the result for the radiative quadrupole moment 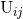 expressed as a functional of the
intermediate canonical moments
expressed as a functional of the
intermediate canonical moments 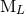 ,
, 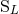 up to 3.5PN order included. The long calculation follows from
implementing the explicit MPM algorithm of Section 2.3 and yields various types of terms:
up to 3.5PN order included. The long calculation follows from
implementing the explicit MPM algorithm of Section 2.3 and yields various types of terms:
- The instantaneous (i.e., non-hereditary) piece
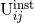 up to 3.5PN order reads
up to 3.5PN order reads
The Newtonian term in this expression contains the Newtonian quadrupole moment
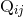 and
recovers the standard quadrupole formalism [see Eq. (67*)];
and
recovers the standard quadrupole formalism [see Eq. (67*)];
- The hereditary tail integral
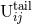 is made of the dominant tail term at 1.5PN order in agreement
with Eq. (76a) above:
is made of the dominant tail term at 1.5PN order in agreement
with Eq. (76a) above:
The length scale
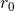 is the one that enters our definition of the finite-part operation
is the one that enters our definition of the finite-part operation 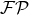 [see
Eq. (42*)] and it enters also the relation between the radiative and harmonic retarded times given by
Eq. (78*);
[see
Eq. (42*)] and it enters also the relation between the radiative and harmonic retarded times given by
Eq. (78*);
- The hereditary tail-of-tail term appears dominantly at 3PN order [48*] and is issued from the radiative metric computed in Eqs. (87):
- Finally the memory-type hereditary piece
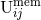 contributes at orders 2.5PN and 3.5PN and is given
by
contributes at orders 2.5PN and 3.5PN and is given
by
The 2.5PN non-linear memory integral – the first term inside the coefficient of 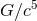 – has been obtained
using both post-Newtonian methods [42, 427*, 406, 60*, 50] and rigorous studies of the field at future null
infinity [128]. The expression (92) is in agreement with the more recent computation of the non-linear
memory up to any post-Newtonian order in Refs. [189*, 192].
– has been obtained
using both post-Newtonian methods [42, 427*, 406, 60*, 50] and rigorous studies of the field at future null
infinity [128]. The expression (92) is in agreement with the more recent computation of the non-linear
memory up to any post-Newtonian order in Refs. [189*, 192].
Be careful to note that the latter post-Newtonian orders correspond to “relative” orders when counted in the local radiation-reaction force, present in the equations of motion: For instance, the 1.5PN tail integral in Eq. (90) is due to a 4PN radiative effect in the equations of motion [58*]; similarly, the 3PN tail-of-tail integral is expected to be associated with some radiation-reaction terms occurring at the 5.5PN order.
Note that  , when expressed in terms of the intermediate moments
, when expressed in terms of the intermediate moments 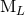 and
and 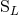 , shows a
dependence on the (arbitrary) length scale
, shows a
dependence on the (arbitrary) length scale 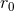 ; cf. the tail and tail-of-tail contributions (90) – (91). Most
of this dependence comes from our definition of a radiative coordinate system as given by (78*). Exactly as
we have done for the 1.5PN tail term in Eq. (79*), we can remove most of the
; cf. the tail and tail-of-tail contributions (90) – (91). Most
of this dependence comes from our definition of a radiative coordinate system as given by (78*). Exactly as
we have done for the 1.5PN tail term in Eq. (79*), we can remove most of the 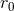 ’s by inserting
’s by inserting
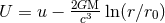 back into (89) – (92), and expanding the result when
back into (89) – (92), and expanding the result when  , keeping the
necessary terms consistently. In doing so one finds that there remains a
, keeping the
necessary terms consistently. In doing so one finds that there remains a 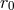 -dependent term at the 3PN
order, namely
-dependent term at the 3PN
order, namely
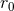 is fictitious and should in fine disappear. The reason is that when
we compute explicitly the mass quadrupole moment
is fictitious and should in fine disappear. The reason is that when
we compute explicitly the mass quadrupole moment 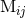 for a given matter source, we will find an extra
contribution depending on
for a given matter source, we will find an extra
contribution depending on  occurring at the 3PN order which will cancel out the one in Eq. (93*).
Indeed we shall compute the source quadrupole moment
occurring at the 3PN order which will cancel out the one in Eq. (93*).
Indeed we shall compute the source quadrupole moment 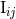 of compact binaries at the 3PN order,
and we do observe on the result (300*) – (301) below the requested terms depending on
of compact binaries at the 3PN order,
and we do observe on the result (300*) – (301) below the requested terms depending on 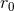 ,
namely27
where
,
namely27
where 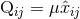 denotes the Newtonian quadrupole,
denotes the Newtonian quadrupole, 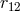 is the separation between the particles, and
is the separation between the particles, and
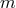 is the total mass differing from the ADM mass
is the total mass differing from the ADM mass 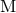 by small post-Newtonian corrections. Combining
Eqs. (93*) and (94*) we see that the
by small post-Newtonian corrections. Combining
Eqs. (93*) and (94*) we see that the 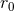 -dependent terms cancel as expected. The appearance of a logarithm
and its associated constant
-dependent terms cancel as expected. The appearance of a logarithm
and its associated constant 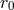 at the 3PN order was pointed out in Ref. [7*]; it was rederived
within the present formalism in Refs. [58*, 48]. Recently a result equivalent to Eq. (93*) was
obtained by means of the EFT approach using considerations related to the renormalization group
equation [222].
at the 3PN order was pointed out in Ref. [7*]; it was rederived
within the present formalism in Refs. [58*, 48]. Recently a result equivalent to Eq. (93*) was
obtained by means of the EFT approach using considerations related to the renormalization group
equation [222].
The previous formulas for the 3.5PN radiative quadrupole moment permit to compute the dominant
mode 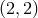 of the waveform up to order 3.5PN [197*]; however, to control the full waveform one has also
to take into account the contributions of higher-order radiative moments. Here we list the most accurate
results we have for all the moments that permit the derivation of the waveform up to order 3PN
[74*]:28
of the waveform up to order 3.5PN [197*]; however, to control the full waveform one has also
to take into account the contributions of higher-order radiative moments. Here we list the most accurate
results we have for all the moments that permit the derivation of the waveform up to order 3PN
[74*]:28
For all the other multipole moments in the 3PN waveform, it is sufficient to assume the agreement between the radiative and canonical moments, namely
In a second stage of the general formalism, we must express the canonical moments 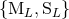 in
terms of the six types of source moments
in
terms of the six types of source moments 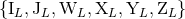 . For the control of the
. For the control of the
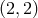 mode in the waveform up to 3.5PN order, we need to relate the canonical quadrupole
moment
mode in the waveform up to 3.5PN order, we need to relate the canonical quadrupole
moment 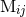 to the corresponding source quadrupole moment
to the corresponding source quadrupole moment 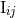 up to that accuracy. We
obtain [197*]
up to that accuracy. We
obtain [197*]
Here, for instance,  denotes the monopole moment associated with the moment
denotes the monopole moment associated with the moment 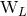 , and
, and 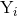 is
the dipole moment corresponding to
is
the dipole moment corresponding to  . Notice that the difference between the canonical and source
moments starts at the relatively high 2.5PN order. For the control of the full waveform up to 3PN order we
need also the moments
. Notice that the difference between the canonical and source
moments starts at the relatively high 2.5PN order. For the control of the full waveform up to 3PN order we
need also the moments 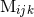 and
and 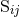 , which admit similarly some correction terms starting at the 2.5PN
order:
, which admit similarly some correction terms starting at the 2.5PN
order:
The remainders in Eqs. (98) are consistent with the 3PN approximation for the full waveform. Besides
the mass quadrupole moment (97), and mass octopole and current quadrupole moments (98), we can state
that, with the required 3PN precision, all the other moments 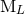 ,
, 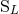 agree with their source
counterparts
agree with their source
counterparts 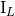 ,
, 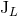 :
:
With those formulas we have related the radiative moments 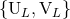 parametrizing the
asymptotic waveform (66) to the six types of source multipole moments
parametrizing the
asymptotic waveform (66) to the six types of source multipole moments 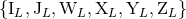 .
What is missing is the explicit dependence of the source moments as functions of the actual
parameters of some matter source. We come to grips with this important question in the next
section.
.
What is missing is the explicit dependence of the source moments as functions of the actual
parameters of some matter source. We come to grips with this important question in the next
section.

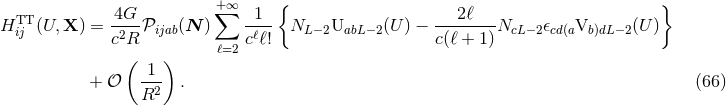

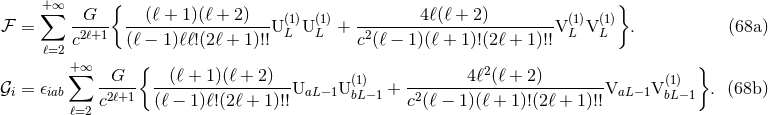

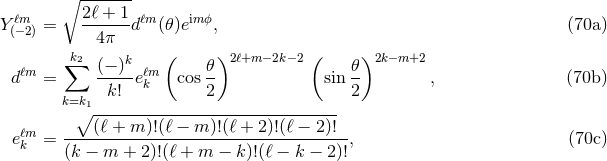
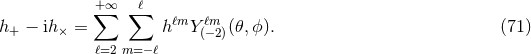
![∫ ℓm [ ]-ℓm h = dΩ h+ − ih× Y(−2)(𝜃,ϕ), (72 )](article626x.gif)
![[ ] ℓm ---G----- ℓm i ℓm h = − √2Rc ℓ+2 U − cV , (73 )](article630x.gif)
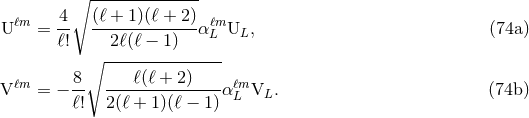
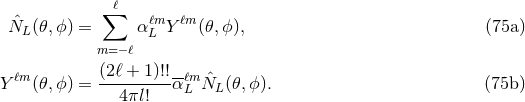
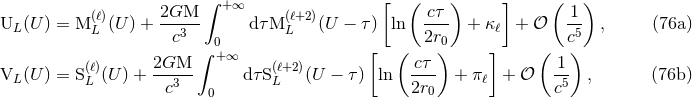
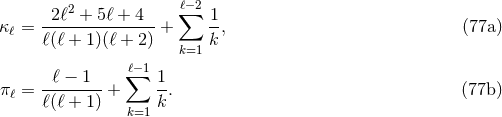
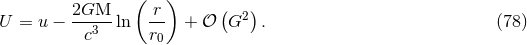
![(ℓ) 2GM ∫ +∞ (ℓ+2) [ (cτ ) ] ( 1 ) UL(U ) = M L (u) + --3-- dτ M L (u − τ) ln --- + κℓ + 𝒪 -5 . (79 ) c 0 2r c](article670x.gif)
![∫ ( ) (ℓ) ′ 2GM + ∞ (l+2 ) ′ [ (cτ ) ′] 1 UL (U ) = M L (u ) + --3-- dτM L (u − τ) ln --′ + κℓ + 𝒪 -5 , (80 ) c 0 2r c](article680x.gif)
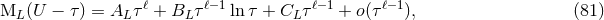

![[ ] ∫ +∞ −1 ˆnL- □ ret r2 F(t − r) = − ˆnL 1 dxQ ℓ(x )F (t − rx ), (83 )](article719x.gif)