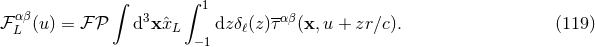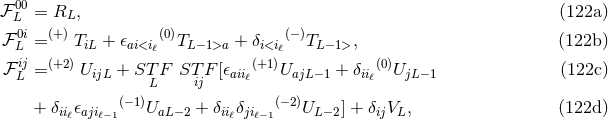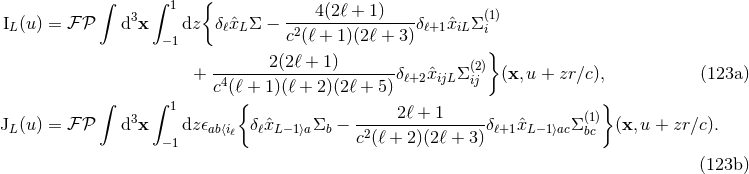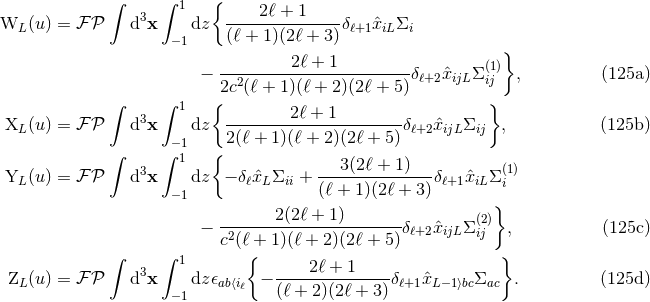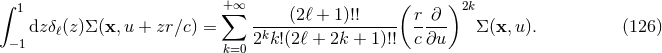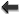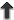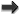4 Matching to a Post-Newtonian Source
By Theorem 2 we control the most general class of solutions of the vacuum equations outside the source, in the form of non-linear functionals of the source multipole moments. For instance, these solutions include the Schwarzschild and Kerr solutions for black holes, as well as all their perturbations. By Theorem 4 we learned how to construct the radiative moments at infinity, which constitute the observables of the radiation field at large distances from the source, and we obtained in Section 3.3 explicit relationships between radiative and source moments. We now want to understand how a specific choice of matter stress-energy tensor , i.e., a specific choice of some physical model describing the material
source, selects a particular physical exterior solution among our general class, and therefore a given set of
multipole moments for the source.
, i.e., a specific choice of some physical model describing the material
source, selects a particular physical exterior solution among our general class, and therefore a given set of
multipole moments for the source.
4.1 The matching equation
We shall provide the answer to that problem in the case of a post-Newtonian source for which the
post-Newtonian parameter 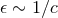 defined by Eq. (1*) is small. The fundamental fact that permits the
connection of the exterior field to the inner field of the source is the existence of a “matching”
region, in which both the multipole expansion and the post-Newtonian expansion are valid.
This region is nothing but the exterior part of the near zone, such that
defined by Eq. (1*) is small. The fundamental fact that permits the
connection of the exterior field to the inner field of the source is the existence of a “matching”
region, in which both the multipole expansion and the post-Newtonian expansion are valid.
This region is nothing but the exterior part of the near zone, such that 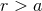 (exterior) and
(exterior) and
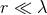 (near zone); it always exists around post-Newtonian sources whose radius is much
less than the emitted wavelength,
(near zone); it always exists around post-Newtonian sources whose radius is much
less than the emitted wavelength, 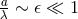 . In our formalism the multipole expansion is
defined by the multipolar-post-Minkowskian (MPM) solution; see Section 2. Matching together
the post-Newtonian and MPM solutions in this overlapping region is an application of the
method of matched asymptotic expansions, which has frequently been applied in the present
context, both for radiation-reaction [114*, 113*, 7, 58*, 43*] and wave-generation [59*, 155, 44*, 49*]
problems.
. In our formalism the multipole expansion is
defined by the multipolar-post-Minkowskian (MPM) solution; see Section 2. Matching together
the post-Newtonian and MPM solutions in this overlapping region is an application of the
method of matched asymptotic expansions, which has frequently been applied in the present
context, both for radiation-reaction [114*, 113*, 7, 58*, 43*] and wave-generation [59*, 155, 44*, 49*]
problems.
Let us denote by 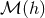 the multipole expansion of
the multipole expansion of 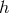 (for simplicity, we suppress the space-time
indices). By
(for simplicity, we suppress the space-time
indices). By 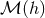 we really mean the MPM exterior metric that we have constructed in Sections 2.2
and 2.3:
we really mean the MPM exterior metric that we have constructed in Sections 2.2
and 2.3:
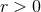 . Of course, the true solution
. Of course, the true solution 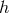 agrees with its own
multipole expansion in the exterior of the source, i.e.
By contrast, inside the source,
agrees with its own
multipole expansion in the exterior of the source, i.e.
By contrast, inside the source, 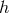 and
and 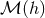 disagree with each other because
disagree with each other because 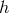 is a fully-fledged
solution of the field equations within the matter source, while
is a fully-fledged
solution of the field equations within the matter source, while 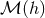 is a vacuum solution becoming
singular at
is a vacuum solution becoming
singular at 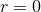 . Now let us denote by
. Now let us denote by  the post-Newtonian expansion of
the post-Newtonian expansion of 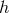 . We have already
anticipated the general structure of this expansion which is given in Eq. (54*). In the matching region, where
both the multipolar and post-Newtonian expansions are valid, we write the numerical equality
This “numerical” equality is viewed here in a sense of formal expansions, as we do not control the
convergence of the series. In fact, we should be aware that such an equality, though quite natural and even
physically obvious, is probably not really justified within the approximation scheme (mathematically
speaking), and we simply take it here as part of our fundamental assumptions.
. We have already
anticipated the general structure of this expansion which is given in Eq. (54*). In the matching region, where
both the multipolar and post-Newtonian expansions are valid, we write the numerical equality
This “numerical” equality is viewed here in a sense of formal expansions, as we do not control the
convergence of the series. In fact, we should be aware that such an equality, though quite natural and even
physically obvious, is probably not really justified within the approximation scheme (mathematically
speaking), and we simply take it here as part of our fundamental assumptions.
We now transform Eq. (102*) into a matching equation, by replacing in the left-hand side 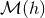 by its
near-zone re-expansion
by its
near-zone re-expansion 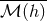 , and in the right-hand side
, and in the right-hand side 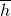 by its multipole expansion
by its multipole expansion 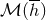 .
The structure of the near-zone expansion (
.
The structure of the near-zone expansion ( ) of the exterior multipolar field has been
found in Theorem 3, see Eq. (53*). We denote the corresponding infinite series
) of the exterior multipolar field has been
found in Theorem 3, see Eq. (53*). We denote the corresponding infinite series  with
the same overbar as for the post-Newtonian expansion because it is really an expansion when
with
the same overbar as for the post-Newtonian expansion because it is really an expansion when
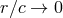 , equivalent to an expansion when
, equivalent to an expansion when 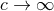 . Concerning the multipole expansion of the
post-Newtonian metric,
. Concerning the multipole expansion of the
post-Newtonian metric, 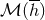 , we simply postulate for the moment its existence, but we shall show
later how to construct it explicitly. Therefore, the matching equation is the statement that
, we simply postulate for the moment its existence, but we shall show
later how to construct it explicitly. Therefore, the matching equation is the statement that
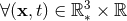 , between the
coefficients of the series in both sides of the equation. Note that such a meaning is somewhat different from
that of a numerical equality like Eq. (102*), which is valid only when
, between the
coefficients of the series in both sides of the equation. Note that such a meaning is somewhat different from
that of a numerical equality like Eq. (102*), which is valid only when 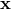 belongs to some limited spatial
domain. The matching equation (103*) tells us that the formal near-zone expansion of the multipole
decomposition is identical, term by term, to the multipole expansion of the post-Newtonian solution.
However, the former expansion is nothing but the formal far-zone expansion, when
belongs to some limited spatial
domain. The matching equation (103*) tells us that the formal near-zone expansion of the multipole
decomposition is identical, term by term, to the multipole expansion of the post-Newtonian solution.
However, the former expansion is nothing but the formal far-zone expansion, when 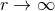 , of each of the
post-Newtonian coefficients. Most importantly, it is possible to write down, within the present
formalism, the general structure of these identical expansions as a consequence of Eq. (53*):
where the functions
, of each of the
post-Newtonian coefficients. Most importantly, it is possible to write down, within the present
formalism, the general structure of these identical expansions as a consequence of Eq. (53*):
where the functions 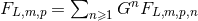 . The latter expansion can be interpreted either as the
singular re-expansion of the multipole decomposition when
. The latter expansion can be interpreted either as the
singular re-expansion of the multipole decomposition when 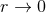 – i.e., the first equality in Eq. (104*)
–, or the singular re-expansion of the post-Newtonian series when
– i.e., the first equality in Eq. (104*)
–, or the singular re-expansion of the post-Newtonian series when 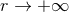 – the second
equality.
– the second
equality.
We recognize the beauty of singular perturbation theory, where two asymptotic expansions, taken
formally outside their respective domains of validity, are matched together. Of course, the method works
because there exists, physically, an overlapping region in which the two approximation series
are expected to be numerically close to the exact solution. As we shall detail in Sections 4.2
and 5.2, the matching equation (103*), supplemented by the condition of no-incoming radiation
[say in the form of Eq. (29*)], permits determining all the unknowns of the problem: On the
one hand, the external multipolar decomposition  , i.e., the explicit expressions of the
multipole moments therein (see Sections 4.2 and 4.4); on the other hand, the terms in the inner
post-Newtonian expansion
, i.e., the explicit expressions of the
multipole moments therein (see Sections 4.2 and 4.4); on the other hand, the terms in the inner
post-Newtonian expansion  that are associated with radiation-reaction effects, i.e., those terms which
depend on the boundary conditions of the radiative field at infinity, and which correspond in the
present case to a post-Newtonian source which is isolated from other sources in the Universe; see
Section 5.2.
that are associated with radiation-reaction effects, i.e., those terms which
depend on the boundary conditions of the radiative field at infinity, and which correspond in the
present case to a post-Newtonian source which is isolated from other sources in the Universe; see
Section 5.2.
4.2 General expression of the multipole expansion
Theorem 5. Under the hypothesis of matching, Eq. (103*), the multipole expansion of the solution of the Einstein field equation outside a post-Newtonian source reads
where the “multipole moments” are given by Here,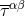 denotes the post-Newtonian expansion of the stress-energy pseudo-tensor in harmonic
coordinates as defined by Eq. (23*).
denotes the post-Newtonian expansion of the stress-energy pseudo-tensor in harmonic
coordinates as defined by Eq. (23*).
Proof (see Refs. [44*, 49*]): First notice where the physical restriction of considering a post-Newtonian
source enters this theorem: The multipole moments (106*) depend on the post-Newtonian expansion 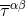 of the pseudo-tensor, rather than on
of the pseudo-tensor, rather than on 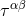 itself. Consider
itself. Consider 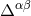 , namely the difference between
, namely the difference between 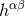 ,
which is a solution of the field equations everywhere inside and outside the source, and the first term in
Eq. (105*), namely the finite part of the retarded integral of the multipole expansion
,
which is a solution of the field equations everywhere inside and outside the source, and the first term in
Eq. (105*), namely the finite part of the retarded integral of the multipole expansion 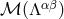 :
:
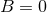 by a
mere
by a
mere 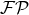 . According to Eq. (30*),
. According to Eq. (30*), 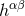 is given by the retarded integral of the pseudo-tensor
is given by the retarded integral of the pseudo-tensor 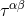 . So,
In the second term the finite part plays a crucial role because the multipole expansion
. So,
In the second term the finite part plays a crucial role because the multipole expansion 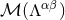 is singular
at
is singular
at 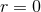 . By contrast, the first term in Eq. (108*), as it stands, is well-defined because we are considering
only some smooth field distributions:
. By contrast, the first term in Eq. (108*), as it stands, is well-defined because we are considering
only some smooth field distributions: 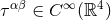 . There is no need to include a finite part
. There is no need to include a finite part 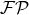 in
the first term, but a contrario there is no harm to add one in front of it, because for convergent integrals
the finite part simply gives back the value of the integral. The advantage of adding artificially
the
in
the first term, but a contrario there is no harm to add one in front of it, because for convergent integrals
the finite part simply gives back the value of the integral. The advantage of adding artificially
the 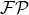 in the first term is that we can re-write Eq. (108*) into the more interesting form
in which we have also used the fact that
in the first term is that we can re-write Eq. (108*) into the more interesting form
in which we have also used the fact that 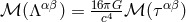 because
because  has a compact support.
The interesting point about Eq. (109*) is that
has a compact support.
The interesting point about Eq. (109*) is that 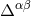 appears now to be the (finite part of a)
retarded integral of a source with spatially compact support. This follows from the fact that the
pseudo-tensor agrees numerically with its own multipole expansion when
appears now to be the (finite part of a)
retarded integral of a source with spatially compact support. This follows from the fact that the
pseudo-tensor agrees numerically with its own multipole expansion when  [by the same
equation as Eq. (102*)]. Therefore,
[by the same
equation as Eq. (102*)]. Therefore, 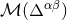 can be obtained from the known formula for
the multipole expansion of the retarded solution of a wave equation with compact-support
source. This formula, given in Appendix B of Ref. [59], yields the second term in Eq. (105*),
but in which the moments do not yet match the result (106*);
instead,29
The reason is that we have not yet applied the assumption of a post-Newtonian source. Such
sources are entirely covered by their own near zone (i.e.,
can be obtained from the known formula for
the multipole expansion of the retarded solution of a wave equation with compact-support
source. This formula, given in Appendix B of Ref. [59], yields the second term in Eq. (105*),
but in which the moments do not yet match the result (106*);
instead,29
The reason is that we have not yet applied the assumption of a post-Newtonian source. Such
sources are entirely covered by their own near zone (i.e.,  ), and, in addition, for them the
integral (111*) has a compact support limited to the domain of the source. In consequence, we can
replace the integrand in Eq. (111*) by its post-Newtonian expansion, valid over all the near zone:
Strangely enough, we do not get the expected result because of the presence of the second term in
Eq. (112*). Actually, this term is a bit curious, because the object
), and, in addition, for them the
integral (111*) has a compact support limited to the domain of the source. In consequence, we can
replace the integrand in Eq. (111*) by its post-Newtonian expansion, valid over all the near zone:
Strangely enough, we do not get the expected result because of the presence of the second term in
Eq. (112*). Actually, this term is a bit curious, because the object 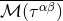 it contains is only
known in the form of the formal series whose structure is given by the first equality in Eq. (104*)
(indeed
it contains is only
known in the form of the formal series whose structure is given by the first equality in Eq. (104*)
(indeed 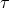 and
and 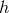 have the same type of structure). Happily – because we would not know
what to do with this term in applications – we are now going to prove that the second term
in Eq. (112*) is in fact identically zero. The proof is based on the properties of the analytic
continuation as applied to the formal structure (104*) of
have the same type of structure). Happily – because we would not know
what to do with this term in applications – we are now going to prove that the second term
in Eq. (112*) is in fact identically zero. The proof is based on the properties of the analytic
continuation as applied to the formal structure (104*) of 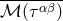 . Each term of this series yields a
contribution to Eq. (112*) that takes the form, after performing the angular integration, of the integral
. Each term of this series yields a
contribution to Eq. (112*) that takes the form, after performing the angular integration, of the integral
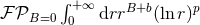 , and multiplied by some function of time. We want to prove that the
radial integral
, and multiplied by some function of time. We want to prove that the
radial integral 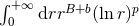 is zero by analytic continuation (
is zero by analytic continuation (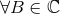 ). First we can
get rid of the logarithms by considering some repeated differentiations with respect to
). First we can
get rid of the logarithms by considering some repeated differentiations with respect to 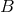 ;
thus we need only to consider the simpler integral
;
thus we need only to consider the simpler integral 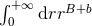 . We split the integral into a
“near-zone” integral
. We split the integral into a
“near-zone” integral 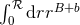 and a “far-zone” one
and a “far-zone” one  , where
, where 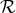 is some constant
radius. When
is some constant
radius. When 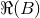 is a large enough positive number, the value of the near-zone integral is
is a large enough positive number, the value of the near-zone integral is
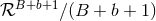 , while when
, while when 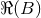 is a large negative number, the far-zone integral reads the
opposite,
is a large negative number, the far-zone integral reads the
opposite, 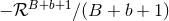 . Both obtained values represent the unique analytic continuations of
the near-zone and far-zone integrals for any
. Both obtained values represent the unique analytic continuations of
the near-zone and far-zone integrals for any 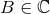 except
except 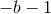 . The complete integral
. The complete integral
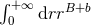 is equal to the sum of these analytic continuations, and is therefore identically zero
(
is equal to the sum of these analytic continuations, and is therefore identically zero
(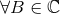 , including the value
, including the value 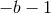 ). At last we have completed the proof of Theorem 5:
). At last we have completed the proof of Theorem 5:
The latter proof makes it clear how crucial the analytic-continuation finite part 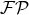 is, which we recall
is the same as in our iteration of the exterior post-Minkowskian field [see Eq. (45*)]. Without a
finite part, the multipole moment (113*) would be strongly divergent, because the pseudo-tensor
is, which we recall
is the same as in our iteration of the exterior post-Minkowskian field [see Eq. (45*)]. Without a
finite part, the multipole moment (113*) would be strongly divergent, because the pseudo-tensor
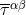 has a non-compact support owing to the contribution of the gravitational field, and the
multipolar factor
has a non-compact support owing to the contribution of the gravitational field, and the
multipolar factor 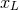 behaves like
behaves like 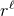 when
when 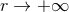 . The latter divergence has plagued the
field of post-Newtonian expansions of gravitational radiation for many years. In applications
such as in Part B of this article, we must carefully follow the rules for handling the
. The latter divergence has plagued the
field of post-Newtonian expansions of gravitational radiation for many years. In applications
such as in Part B of this article, we must carefully follow the rules for handling the 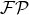 operator.
operator.
The two terms in the right-hand side of Eq. (105*) depend separately on the length scale  that we
have introduced into the definition of the finite part, through the analytic-continuation factor
that we
have introduced into the definition of the finite part, through the analytic-continuation factor
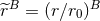 introduced in Eq. (42*). However, the sum of these two terms, i.e., the exterior multipolar
field
introduced in Eq. (42*). However, the sum of these two terms, i.e., the exterior multipolar
field 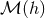 itself, is independent of
itself, is independent of 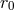 . To see this, the simplest way is to differentiate
formally
. To see this, the simplest way is to differentiate
formally 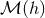 with respect to
with respect to 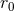 ; the differentiations of the two terms of Eq. (105*) cancel
each other. The independence of the field upon
; the differentiations of the two terms of Eq. (105*) cancel
each other. The independence of the field upon 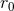 is quite useful in applications, since in
general many intermediate calculations do depend on
is quite useful in applications, since in
general many intermediate calculations do depend on 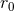 , and only in the final stage does the
cancellation of the
, and only in the final stage does the
cancellation of the 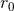 ’s occur. For instance, we have already seen in Eqs. (93*) – (94*) that the
source quadrupole moment
’s occur. For instance, we have already seen in Eqs. (93*) – (94*) that the
source quadrupole moment  depends on
depends on 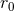 starting from the 3PN level, but that this
starting from the 3PN level, but that this
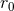 is compensated by another
is compensated by another 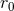 coming from the non-linear “tails of tails” at the 3PN
order.
coming from the non-linear “tails of tails” at the 3PN
order.
4.3 Equivalence with the Will–Wiseman formalism
Will & Wiseman [424*] (see also Refs. [422, 335]), extending previous work of Epstein & Wagoner [185] and Thorne [403], have obtained a different-looking multipole decomposition, with different definitions for the multipole moments of a post-Newtonian source. They find, instead of our multipole decomposition given by Eq. (105*),
There is no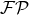 operation in the first term, but instead the retarded integral is truncated, as
indicated by the subscript
operation in the first term, but instead the retarded integral is truncated, as
indicated by the subscript 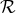 , to extend only in the “far zone”: i.e.,
, to extend only in the “far zone”: i.e., 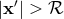 in the notation
of Eq. (31*), where
in the notation
of Eq. (31*), where 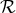 is a constant radius enclosing the source (
is a constant radius enclosing the source (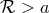 ). The near-zone
part of the retarded integral is thereby removed, and there is no problem with the singularity
of the multipole expansion
). The near-zone
part of the retarded integral is thereby removed, and there is no problem with the singularity
of the multipole expansion 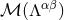 at the origin. The multipole moments
at the origin. The multipole moments 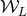 are then
given, in contrast with our result (106*), by an integral extending over the “near zone” only:
Since the integrand is compact-supported there is no problem with the bound at infinity and the integral is
well-defined (no need of a
are then
given, in contrast with our result (106*), by an integral extending over the “near zone” only:
Since the integrand is compact-supported there is no problem with the bound at infinity and the integral is
well-defined (no need of a 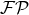 ).
).
Let us show that the two different formalisms are equivalent. We compute the difference between our
moment 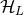 defined by Eq. (106*), and the moment
defined by Eq. (106*), and the moment 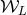 given by Eq. (115*). For the comparison we
split
given by Eq. (115*). For the comparison we
split 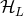 into far-zone and near-zone pieces corresponding to the radius
into far-zone and near-zone pieces corresponding to the radius 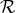 . Since the finite part
. Since the finite part 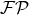 present in
present in 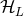 deals only with the bound at infinity, it can be removed from the near-zone piece, which is
then seen to reproduce
deals only with the bound at infinity, it can be removed from the near-zone piece, which is
then seen to reproduce 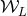 exactly. So the difference between the two moments is simply given by the
far-zone piece:
exactly. So the difference between the two moments is simply given by the
far-zone piece:
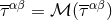 because we are outside the
source, and
because we are outside the
source, and 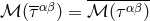 thanks to the matching equation (103*). At this stage, we recall from our
reasoning right after Eq. (112*) that the finite part of an integral over the whole space
thanks to the matching equation (103*). At this stage, we recall from our
reasoning right after Eq. (112*) that the finite part of an integral over the whole space 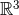 of a quantity
having the same structure as
of a quantity
having the same structure as  is identically zero by analytic continuation. The main ingredient of
the present proof is made possible by this fact, as it allows us to transform the far-zone integration
is identically zero by analytic continuation. The main ingredient of
the present proof is made possible by this fact, as it allows us to transform the far-zone integration
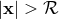 in Eq. (116*) into a near-zone one
in Eq. (116*) into a near-zone one 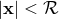 , at the price of changing the overall sign in front of
the integral. So,
Finally, it is straightforward to check that the right-hand side of this equation, when summed up over all
multipolarities
, at the price of changing the overall sign in front of
the integral. So,
Finally, it is straightforward to check that the right-hand side of this equation, when summed up over all
multipolarities  , accounts exactly for the near-zone part that was removed from the retarded integral of
, accounts exactly for the near-zone part that was removed from the retarded integral of
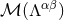 in the first term in Eq. (114*), so that the “complete” retarded integral as given by the first term
in our own definition (105*) is exactly reconstituted. In conclusion, the formalism of Ref. [424*] is equivalent
to the one of Refs. [44*, 49].
in the first term in Eq. (114*), so that the “complete” retarded integral as given by the first term
in our own definition (105*) is exactly reconstituted. In conclusion, the formalism of Ref. [424*] is equivalent
to the one of Refs. [44*, 49].
4.4 The source multipole moments
In principle, the bridge between the exterior gravitational field generated by the post-Newtonian
source and its inner field is provided by Theorem 5; however, we still have to make the
connection with the explicit construction of the general multipolar and post-Minkowskian
metric in Section 2. Namely, we must find the expressions of the six STF source multipole
moments 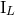 ,
, 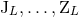 parametrizing the linearized metric (35*) – (37) at the basis of that
construction.30
parametrizing the linearized metric (35*) – (37) at the basis of that
construction.30
To do this we first find the equivalent of the multipole expansion given in Theorem 5, which was
parametrized by non-trace-free multipole functions 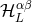 , in terms of new multipole functions
, in terms of new multipole functions 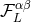 that
are STF in all their indices
that
are STF in all their indices 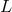 . The result is
. The result is
![ˆxL ≡ STF [xL]](article976x.gif) ) read
Notice the presence of an extra integration variable
) read
Notice the presence of an extra integration variable  , ranging from
, ranging from 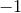 to
to  . The
. The  -integration
involves the weighting function
which approaches the Dirac delta-function (hence its name) in the limit of large multipolarities,
-integration
involves the weighting function
which approaches the Dirac delta-function (hence its name) in the limit of large multipolarities,
 , and is normalized in such a way that
The next step is to impose the harmonic-gauge conditions (21*) onto the multipole decomposition (118*),
and to decompose the multipole functions
, and is normalized in such a way that
The next step is to impose the harmonic-gauge conditions (21*) onto the multipole decomposition (118*),
and to decompose the multipole functions 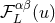 into STF irreducible pieces with respect to both
into STF irreducible pieces with respect to both 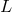 and their spatial indices contained into
and their spatial indices contained into 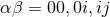 . This technical part of the calculation is identical
to the one of the STF irreducible multipole moments of linearized gravity [154]. The formulas needed in
this decomposition read
. This technical part of the calculation is identical
to the one of the STF irreducible multipole moments of linearized gravity [154]. The formulas needed in
this decomposition read
where the ten tensors  are STF, and are uniquely given in
terms of the
are STF, and are uniquely given in
terms of the 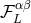 ’s by some inverse formulas. Finally, the latter decompositions yield the
following.
’s by some inverse formulas. Finally, the latter decompositions yield the
following.
Theorem 6. The STF multipole moments 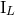 and
and  of a post-Newtonian source are given, formally
up to any post-Newtonian order, by (
of a post-Newtonian source are given, formally
up to any post-Newtonian order, by (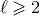 )
)
These moments are the ones that are to be inserted into the linearized metric 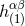 that represents the
lowest approximation to the post-Minkowskian field
that represents the
lowest approximation to the post-Minkowskian field 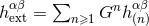 defined in Eq. (50*).
defined in Eq. (50*).
In these formulas the notation is as follows: Some convenient source densities are defined from the
post-Newtonian expansion (denoted by an overbar) of the pseudo-tensor 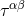 by
by
(where 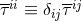 ). As indicated in Eqs. (123) all these quantities are to be evaluated at the spatial
point
). As indicated in Eqs. (123) all these quantities are to be evaluated at the spatial
point 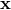 and at time
and at time 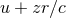 .
.
For completeness, we give also the formulas for the four auxiliary source moments 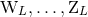 , which
parametrize the gauge vector
, which
parametrize the gauge vector 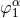 as defined in Eqs. (37):
as defined in Eqs. (37):
As discussed in Section 2, one can always find two intermediate “packages” of multipole moments,
namely the canonical moments 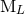 and
and 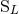 , which are some non-linear functionals of the source
moments (123) and (125), and such that the exterior field depends only on them, modulo a change of
coordinates. However, the canonical moments
, which are some non-linear functionals of the source
moments (123) and (125), and such that the exterior field depends only on them, modulo a change of
coordinates. However, the canonical moments  ,
, 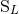 do not admit general closed-form expressions
like (123) – (125).31
do not admit general closed-form expressions
like (123) – (125).31
These source moments are physically valid for post-Newtonian sources and make sense only in the form
of a post-Newtonian expansion, so in practice we need to know how to expand the  -integrals as series
when
-integrals as series
when  . Here is the appropriate formula:
. Here is the appropriate formula:
 , the same result holds equally
well for the advanced variable
, the same result holds equally
well for the advanced variable 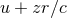 or the retarded one
or the retarded one  . Of course, in the
Newtonian limit, the moments
. Of course, in the
Newtonian limit, the moments 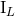 and
and 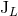 (and also
(and also  and
and 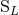 ) reduce to the standard
Newtonian expressions. For instance,
) reduce to the standard
Newtonian expressions. For instance, 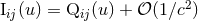 recovers the Newtonian quadrupole
moment (3*).32
recovers the Newtonian quadrupole
moment (3*).32
Needless to say, the formalism becomes prohibitively difficult to apply at very high post-Newtonian
approximations. Some post-Newtonian order being given, we must first compute the relevant relativistic
corrections to the pseudo stress-energy-tensor  ; this necessitates solving the field equations inside the
matter, which we shall investigate in the next Section 5. Then
; this necessitates solving the field equations inside the
matter, which we shall investigate in the next Section 5. Then 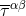 is to be inserted into the source
moments (123) and (125), where the formula (126*) permits expressing all the terms up to that
post-Newtonian order by means of more tractable integrals extending over
is to be inserted into the source
moments (123) and (125), where the formula (126*) permits expressing all the terms up to that
post-Newtonian order by means of more tractable integrals extending over 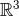 . Given a specific model for
the matter source we then have to find a way to compute all these spatial integrals; this is done in
Section 9.1 for the case of point-mass binaries. Next, we must substitute the source multipole moments into
the linearized metric (35*) – (37), and iterate them until all the necessary multipole interactions taking place
in the radiative moments
. Given a specific model for
the matter source we then have to find a way to compute all these spatial integrals; this is done in
Section 9.1 for the case of point-mass binaries. Next, we must substitute the source multipole moments into
the linearized metric (35*) – (37), and iterate them until all the necessary multipole interactions taking place
in the radiative moments 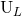 and
and 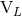 are under control. In fact, we have already worked out
these multipole interactions for general sources in Section 3.3 up to the 3PN order in the full
waveform, and 3.5PN order for the dominant
are under control. In fact, we have already worked out
these multipole interactions for general sources in Section 3.3 up to the 3PN order in the full
waveform, and 3.5PN order for the dominant 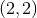 mode. Only at this point does one have the
physical radiation field at infinity, from which we can build the templates for the detection and
analysis of gravitational waves. We advocate here that the complexity of the formalism simply
reflects the complexity of the Einstein field equations. It is probably impossible to devise a
different formalism, valid for general sources devoid of symmetries, that would be substantially
simpler.
mode. Only at this point does one have the
physical radiation field at infinity, from which we can build the templates for the detection and
analysis of gravitational waves. We advocate here that the complexity of the formalism simply
reflects the complexity of the Einstein field equations. It is probably impossible to devise a
different formalism, valid for general sources devoid of symmetries, that would be substantially
simpler.

![+∞ ∑ n ℳ (h) ≡ hext = G h (n)[IL,...,ZL]. (100 ) n=1](article838x.gif)



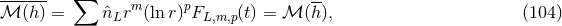
![[ ] 4G +∑∞ (− )ℓ { 1 αβ } ℳ (hαβ) = ℱ 𝒫B=0 □ −r1et^rB ℳ (Λαβ) − --4 ----∂L -ℋ L (t − r∕c) , (105 ) c ℓ=0 ℓ! r](article869x.gif)
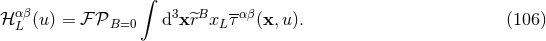
![Δαβ ≡ hαβ − ℱ 𝒫□ − 1[ℳ (Λαβ)]. (107 ) ret](article877x.gif)
![αβ 16-πG- −1 αβ − 1[ αβ ] Δ = c4 □ retτ − ℱ 𝒫 □ret ℳ (Λ ) . (108 )](article882x.gif)
![Δ αβ = 16πG--ℱ 𝒫□ −1 [ταβ − ℳ (τ αβ)], (109 ) c4 ret](article888x.gif)

![αβ ∫ [ ] ℋ L = ℱ 𝒫 d3xxL ταβ − ℳ (τ αβ) . (111 )](article897x.gif)
![∫ αβ 3 [-αβ -----αβ-] ℋ L = ℱ 𝒫 d xxL τ − ℳ (τ ) . (112 )](article899x.gif)

![[ ] 4G ∑+∞ (− )ℓ { 1 } ℳ (hαβ) = □ −r1et ℳ (Λαβ ) − --- -----∂L -𝒲 αLβ (t − r∕c) . (114 ) ℛ c4 ℓ=0 ℓ! r](article941x.gif)
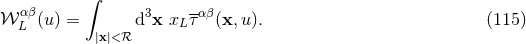
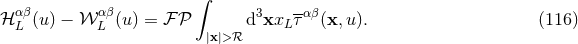
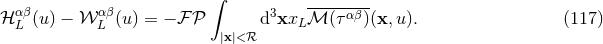
![[ ] 4G +∑∞ (− )ℓ { 1 αβ } ℳ (hαβ) = ℱ 𝒫 □ −re1t ℳ (Λαβ) − --4 ----∂L -ℱ L (t − r∕c) , (118 ) c ℓ=0 ℓ! r](article975x.gif)