List of Footnotes
| 1 | A few errata have been published in this intricate field; all formulas take into account the latest changes. | |
| 2 | In this article Greek indices 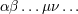 take space-time values 0, 1, 2, 3 and Latin indices take space-time values 0, 1, 2, 3 and Latin indices 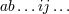 spatial values 1,
2, 3. Cartesian coordinates are assumed throughout and boldface notation is often used for ordinary Euclidean vectors. In
Section 11 upper Latin letters spatial values 1,
2, 3. Cartesian coordinates are assumed throughout and boldface notation is often used for ordinary Euclidean vectors. In
Section 11 upper Latin letters 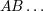 will refer to tetrad indices 0, 1, 2, 3 with will refer to tetrad indices 0, 1, 2, 3 with 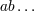 the corresponding spatial values 1, 2,
3. Our signature is +2; hence the Minkowski metric reads the corresponding spatial values 1, 2,
3. Our signature is +2; hence the Minkowski metric reads 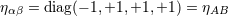 . As usual . As usual  and and  are
Newton’s constant and the speed of light. are
Newton’s constant and the speed of light. |
|
| 3 | Establishing the post-Newtonian expansion rigorously has been the subject of numerous mathematically oriented works, see e.g., [361*, 362*, 363*]. | |
| 4 | Note that for very eccentric binaries (with say  ) the Newtonian potential ) the Newtonian potential  can be numerically much larger
than the estimate can be numerically much larger
than the estimate 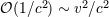 at the apastron of the orbit. at the apastron of the orbit. |
|
| 5 | Whereas, the direct attack of the post-Minkowskian expansion, valid at once inside and outside the source, faces some calculational difficulties [408, 136]. | |
| 6 | The TT coordinate system can be extended to the near zone of the source as well; see for instance Ref. [282]. | |
| 7 | Namely 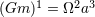 , where , where  is the total mass and is the total mass and 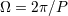 is the orbital frequency. This law is
also appropriately called the 1-2-3 law [319*]. is the orbital frequency. This law is
also appropriately called the 1-2-3 law [319*]. |
|
| 8 | This work entitled: “The last three minutes: Issues in gravitational-wave measurements of coalescing compact binaries” is sometimes coined the “3mn Caltech paper”. | |
| 9 | All the works reviewed in this section concern general relativity. However, let us mention here that the equations of motion of compact binaries in scalar-tensor theories are known up to 2.5PN order [318]. | |
| 10 | The effective action should be equivalent, in the tree-level approximation, to the Fokker action [207], for which the field degrees of freedom (i.e., the metric), that are solutions of the field equations derived from the original matter + field action with gauge-fixing term, have been inserted back into the action, thus defining the Fokker action for the sole matter fields. | |
| 11 | This reference has an eloquent title: “Feynman graph derivation of the Einstein quadrupole formula”. | |
| 12 | In absence of a better terminology, we refer to the leading-order contribution to the recoil as “Newtonian”, although it really corresponds to a 3.5PN subdominant radiation-reaction effect in the binary’s equations of motion. | |
| 13 | Considering the coordinates 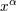 as a set of four scalars, a simple calculation shows that as a set of four scalars, a simple calculation shows that
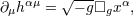 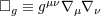 denotes the curved d’Alembertian operator. Hence the harmonic-coordinate condition tells that the
coordinates denotes the curved d’Alembertian operator. Hence the harmonic-coordinate condition tells that the
coordinates 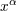 themselves, considered as scalars, are harmonic, i.e., obey the vacuum (curved) d’Alembertian
equation. themselves, considered as scalars, are harmonic, i.e., obey the vacuum (curved) d’Alembertian
equation. |
|
| 14 | In 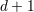 space-time dimensions, only one coefficient in this expression is modified; see Eq. (175) below. space-time dimensions, only one coefficient in this expression is modified; see Eq. (175) below. |
|
| 15 | See Eqs. (3.8) in Ref. [71*] for the cubic and quartic terms. We denote e.g., 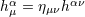 , , 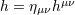 , and , and
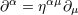 . A parenthesis around a pair of indices denotes the usual symmetrization: . A parenthesis around a pair of indices denotes the usual symmetrization: 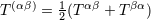 . . |
|
| 16 | 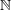 , , 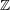 , , 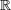 , and , and 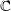 are the usual sets of non-negative integers, integers, real numbers, and complex numbers; are the usual sets of non-negative integers, integers, real numbers, and complex numbers; 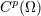 is the set of
is the set of 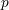 -times continuously differentiable functions on the open domain -times continuously differentiable functions on the open domain 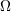 ( (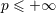 ). ). |
|
| 17 | Our notation is the following: 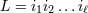 denotes a multi-index, made of denotes a multi-index, made of 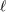 (spatial) indices. Similarly, we write for
instance (spatial) indices. Similarly, we write for
instance 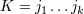 (in practice, we generally do not need to write explicitly the “carrier” letter (in practice, we generally do not need to write explicitly the “carrier” letter 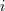 or or 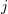 ), or ), or
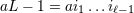 . Always understood in expressions such as Eq. (34*) are . Always understood in expressions such as Eq. (34*) are 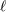 summations over the indices summations over the indices 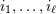 ranging from 1 to 3. The derivative operator
ranging from 1 to 3. The derivative operator 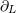 is a short-hand for is a short-hand for 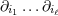 . The function . The function 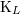 (for any space-time
indices (for any space-time
indices 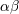 ) is symmetric and trace-free (STF) with respect to the ) is symmetric and trace-free (STF) with respect to the 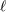 indices composing indices composing 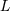 . This means that for any pair
of indices . This means that for any pair
of indices 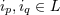 , we have , we have 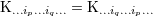 and that and that 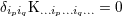 (see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so (see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so  , or sometimes with carets around the indices, , or sometimes with carets around the indices, 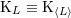 . In particular, . In particular, 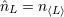 is the
STF projection of the product of unit vectors is the
STF projection of the product of unit vectors 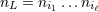 , for instance , for instance 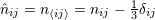 and and
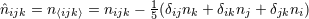 ; an expansion into STF tensors ; an expansion into STF tensors 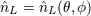 is equivalent to the usual
expansion in spherical harmonics is equivalent to the usual
expansion in spherical harmonics 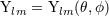 , see Eqs. (75) below. Similarly, we denote , see Eqs. (75) below. Similarly, we denote  where where
 , and , and ![ˆxL = x⟨L⟩ = STF [xL]](article273x.gif) . The Levi-Civita antisymmetric symbol is denoted . The Levi-Civita antisymmetric symbol is denoted 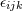 (with (with  ).
Parenthesis refer to symmetrization, ).
Parenthesis refer to symmetrization,  . Superscripts . Superscripts  indicate indicate  successive time
derivations. successive time
derivations. |
|
| 18 | The constancy of the center of mass 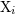 – rather than a linear variation with time – results from our assumption of
stationarity before the date – rather than a linear variation with time – results from our assumption of
stationarity before the date 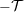 , see Eq. (29*). Hence, , see Eq. (29*). Hence, 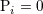 . . |
|
| 19 | This assumption is justified because we are ultimately interested in the radiation field at some given finite
post-Newtonian precision like 3PN, and because only a finite number of multipole moments can contribute
at any finite order of approximation. With a finite number of multipoles in the linearized metric (35*) – (37),
there is a maximal multipolarity 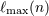 at any post-Minkowskian order at any post-Minkowskian order  , which grows linearly with , which grows linearly with
 . . |
|
| 20 | We employ the Landau symbol  for remainders with its standard meaning. Thus, for remainders with its standard meaning. Thus, ![f(r) = o[g(r)]](article521x.gif) when when 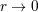 means
that means
that 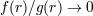 when when 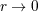 . Furthermore, we generally assume some differentiability properties such as . Furthermore, we generally assume some differentiability properties such as
![dnf (r)∕drn = o[g(r)∕rn]](article525x.gif) . . |
|
| 21 | In this proof the coordinates are considered as dummy variables denoted 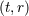 . At the end, when we obtain the radiative
metric, we shall denote the associated radiative coordinates by . At the end, when we obtain the radiative
metric, we shall denote the associated radiative coordinates by 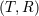 . . |
|
| 22 | The STF tensorial coefficient 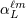 can be computed as can be computed as 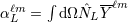 . Our notation is related to that used in
Refs. [403*, 272*] by . Our notation is related to that used in
Refs. [403*, 272*] by 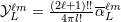 . . |
|
| 23 | The function 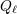 is given in terms of the Legendre polynomial is given in terms of the Legendre polynomial 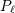 by by
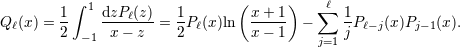  to 1. The first equality is known as the Neumann formula for the
Legendre function. to 1. The first equality is known as the Neumann formula for the
Legendre function. |
|
| 24 | We pose 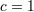 until the end of this section. until the end of this section. |
|
| 25 | The equation (85) has been obtained using a not so well known mathematical relation between the Legendre functions and
polynomials:
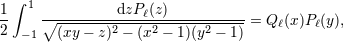  is assumed. See Appendix A in Ref. [48*] for the proof. This relation constitutes a generalization of the
Neumann formula (see the footnote 23). is assumed. See Appendix A in Ref. [48*] for the proof. This relation constitutes a generalization of the
Neumann formula (see the footnote 23). |
|
| 26 | The neglected remainders are indicated by 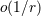 rather than rather than 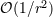 because they contain powers of the logarithm
of because they contain powers of the logarithm
of  ; in fact they could be more accurately written as ; in fact they could be more accurately written as 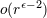 for some for some 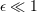 . . |
|
| 27 | The canonical moment 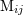 differs from the source moment differs from the source moment 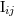 by small 2.5PN and 3.5PN terms; see
Eq. (97). by small 2.5PN and 3.5PN terms; see
Eq. (97). |
|
| 28 | In all formulas below the STF projection 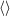 applies only to the “free” indices denoted applies only to the “free” indices denoted 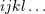 carried by the moments
themselves. Thus the dummy indices such as carried by the moments
themselves. Thus the dummy indices such as 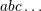 are excluded from the STF projection. are excluded from the STF projection. |
|
| 29 | Recall that our abbreviated notation 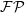 includes the crucial regularization factor includes the crucial regularization factor 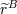 . . |
|
| 30 | Recall that in actual applications we need mostly the mass-type moment 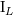 and current-type one and current-type one 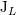 , because the
other moments simply parametrize a linearized gauge transformation. , because the
other moments simply parametrize a linearized gauge transformation. |
|
| 31 | The work [65*] provided some alternative expressions for all the multipole moments (123) – (125), useful for some applications, in the form of surface integrals extending on the outer part of the source’s near zone. | |
| 32 | The moments 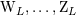 have also a Newtonian limit, but which is not particularly illuminating. have also a Newtonian limit, but which is not particularly illuminating. |
|
| 33 | For this argument we assume the validity of the matching equation (103*) and that the post-Minkowskian series over
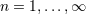 in Eq. (53*) has been formally summed up. in Eq. (53*) has been formally summed up. |
|
| 34 | We mean the fully-fledge 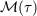 ; i.e., not the formal object ; i.e., not the formal object  . . |
|
| 35 | Though the latter integral is a priori divergent, its value can be determined by invoking complex analytic continuation in
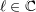 . . |
|
| 36 | Of course the geodesic equations are appropriate for the motion of particles without spins; for spinning particles one has also to take into account the coupling of the spin to the space-time curvature, see Eq. (377*). | |
| 37 | Note, however, that the operation of order-reduction is illicit at the level of the Lagrangian. In fact, it is known that the elimination of acceleration terms in a Lagrangian by substituting the equations of motion derived from that Lagrangian, results in a different Lagrangian whose equations of motion differ from those of the original Lagrangian by a gauge transformation [374]. | |
| 38 | Recall the footnote 17 for our notation. In particular 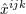 in the vector potential denotes the STF combination in the vector potential denotes the STF combination
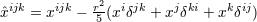 with with 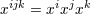 . . |
|
| 39 | The function 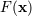 depends also on (coordinate) time depends also on (coordinate) time 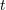 , through for instance its dependence on the velocities , through for instance its dependence on the velocities 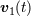 and
and 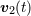 , but the time , but the time  is purely “spectator” in the regularization process, and thus will not be indicated. See the
footnote 20 for the definition of the Landau symbol is purely “spectator” in the regularization process, and thus will not be indicated. See the
footnote 20 for the definition of the Landau symbol  for remainders. for remainders. |
|
| 40 | The sum over 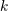 in Eq. (168*) is always finite since there is a maximal order in Eq. (168*) is always finite since there is a maximal order 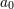 of divergency in Eq. (159*). of divergency in Eq. (159*). |
|
| 41 | It was shown in Ref. [71*] that using one or the other of these derivatives results in some equations of motion that differ by a coordinate transformation, and the redefinition of some ambiguity parameter. This indicates that the distributional derivatives introduced in Ref. [70*] constitute some technical tools devoid of physical meaning besides precisely the appearance of Hadamard’s ambiguity parameters. | |
| 42 | Note also that the harmonic-coordinates 3PN equations of motion [69*, 71*] depend, in addition to 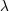 , on two
arbitrary constants , on two
arbitrary constants 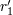 and and 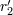 parametrizing some logarithmic terms. These constants are closely related to the
constants parametrizing some logarithmic terms. These constants are closely related to the
constants 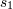 and and  in the partie-finie integral (162*); see Ref. [71*] and Eq. (185*) below for the precise
definition. However, in the partie-finie integral (162*); see Ref. [71*] and Eq. (185*) below for the precise
definition. However,  and and 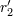 are not “physical” in the sense that they can be removed by a coordinate
transformation. are not “physical” in the sense that they can be removed by a coordinate
transformation. |
|
| 43 | One may wonder why the value of 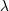 is a complicated rational fraction while is a complicated rational fraction while 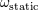 is so simple. This is because is so simple. This is because
 was introduced precisely to measure the amount of ambiguities of certain integrals, while by contrast, was introduced precisely to measure the amount of ambiguities of certain integrals, while by contrast, 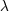 was
introduced [see Eq. (185*)] as an unknown constant entering the relation between the arbitrary scales was
introduced [see Eq. (185*)] as an unknown constant entering the relation between the arbitrary scales  on
the one hand, and on
the one hand, and 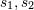 on the other hand, which has a priori nothing to do with the ambiguous part of
integrals. on the other hand, which has a priori nothing to do with the ambiguous part of
integrals. |
|
| 44 | See however some comments on the latter work in Ref. [145], pp. 168 – 169. | |
| 45 | The result for 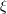 happens to be amazingly related to the one for happens to be amazingly related to the one for 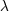 by a cyclic permutation of digits; compare by a cyclic permutation of digits; compare
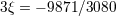 with with 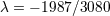 . . |
|
| 46 | In higher approximations there will be also IR divergences and one should really employ the  -dimensional version of
Eq. (141*). -dimensional version of
Eq. (141*). |
|
| 47 | We have 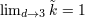 . Notice that . Notice that 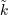 is closely linked to the volume is closely linked to the volume 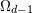 of the sphere with of the sphere with  dimensions (i.e.
embedded into Euclidean dimensions (i.e.
embedded into Euclidean 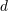 -dimensional space): -dimensional space):
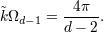 |
|
| 48 | When working at the level of the equations of motion (not considering the metric outside the world-lines), the effect of shifts can be seen as being induced by a coordinate transformation of the bulk metric as in Ref. [71*]. | |
| 49 | Notice the dependence upon the irrational number 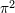 . Technically, the . Technically, the 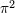 terms arise from non-linear interactions
involving some integrals such as terms arise from non-linear interactions
involving some integrals such as
 |
|
| 50 | On the other hand, the ADM-Hamiltonian formalism provides a limited description of the gravitational radiation field, compared to what will be done using harmonic coordinates in Section 9. | |
| 51 | This parameter is an invariant in a large class of coordinate systems – those for which the metric becomes asymptotically
Minkowskian far from the system:  . . |
|
| 52 | Namely,
![Schw 2 [ 1− 2x ] E = μc √1-−-3x − 1 .](article1828x.gif) |
|
| 53 | From the thermodynamic relation (235*) we necessarily have the relations 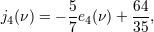  |
|
| 54 | In all of Section 8 we pose 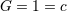 . . |
|
| 55 | Note that this is an iterative process because the masses in Eq. (247*) are themselves to be replaced by the irreducible masses. | |
| 56 | In Ref. [51*] it was assumed that the corotation condition was given by the leading-order result  . The 1PN
correction in Eq. (247*) modifies the 3PN terms in Eq. (250*) with respect to the result of Ref. [51*]. . The 1PN
correction in Eq. (247*) modifies the 3PN terms in Eq. (250*) with respect to the result of Ref. [51*]. |
|
| 57 | One should not confuse the circular-orbit radius 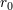 with the constant with the constant 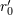 entering the logarithm at the 3PN order in
Eq. (228) and which is defined by Eq. (221*). entering the logarithm at the 3PN order in
Eq. (228) and which is defined by Eq. (221*). |
|
| 58 | This tendency is in agreement with numerical and analytical self-force calculations [24, 287]. | |
| 59 | The first law (280*) has also been generalized for binary systems of point masses moving along generic stable bound (eccentric) orbits in Ref. [286]. | |
| 60 | In the case of extended material bodies, 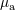 would represent the baryonic mass of the bodies. would represent the baryonic mass of the bodies. |
|
| 61 | Since there are logarithms in this expansion we use the Landau  -symbol for remainders; see the footnote 20. -symbol for remainders; see the footnote 20. |
|
| 62 | In addition, the wave generation formalism will provide the waveform itself, see Sections 9.4 and 9.5. | |
| 63 | The STF projection 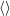 applies only on “living” indices applies only on “living” indices 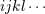 but not on the summed up indices but not on the summed up indices  and and
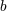 . . |
|
| 64 | The same argument shows that the non-linear multipole interactions in Eq. (89) as well as those in Eqs. (97) and (98) do not contribute to the flux for circular orbits. | |
| 65 | Or, rather, 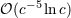 as shown in the Appendix of Ref. [87*]. as shown in the Appendix of Ref. [87*]. |
|
| 66 | See Section 10 for the generalization of the flux of energy to eccentric binary orbits. | |
| 67 | Notice the “strange” post-Newtonian order of this time variable: 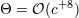 . . |
|
| 68 | This procedure for computing analytically the orbital phase corresponds to what is called in the jargon the “Taylor T2 approximant”. We refer to Ref. [98] for discussions on the usefulness of defining several types of approximants for computing (in general numerically) the orbital phase. | |
| 69 | Notice the obvious fact that the polarization waveforms remain invariant when we rotate by  the separation direction
between the particles and simultaneously exchange the labels of the two particles, i.e., when we apply the transformation the separation direction
between the particles and simultaneously exchange the labels of the two particles, i.e., when we apply the transformation
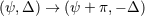 . Moreover, due to the parity invariance, the . Moreover, due to the parity invariance, the 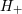 ’s are unchanged after the replacement ’s are unchanged after the replacement 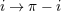 ,
while the ,
while the 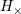 ’s being the projection of ’s being the projection of 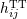 on a tensorial product of two vectors of inverse parity types, is changed into its
opposite. on a tensorial product of two vectors of inverse parity types, is changed into its
opposite. |
|
| 70 | The dependence on 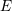 and and 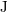 will no longer be indicated but is always understood as implicit in what
follows. will no longer be indicated but is always understood as implicit in what
follows. |
|
| 71 | Comparing with Eqs. (338) we have also
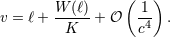 |
|
| 72 | Note that this post-Newtonian parameter  is precisely specified by Eq. (344a), while we only intended to define is precisely specified by Eq. (344a), while we only intended to define  in
Eq. (1*) as representing a post-Newtonian estimate. in
Eq. (1*) as representing a post-Newtonian estimate. |
|
| 73 | More precisely, 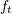 , , 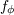 , , 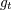 , , 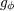 are composed of 2PN and 3PN terms, but are composed of 2PN and 3PN terms, but 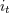 , , 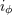 , , 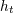 , , 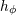 start only at 3PN
order. start only at 3PN
order. |
|
| 74 | On the other hand, for the computation of the gravitational waveform of eccentric binary orbits up to the 2PN order in the Fourier domain, see Refs. [401, 402]. | |
| 75 | Recall that the fluxes are defined in a general way, for any matter system, in terms of the radiative multipole moments by the expressions (68). | |
| 76 | The second of these formulas can alternatively be written with the standard Legendre polynomial 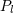 as
as
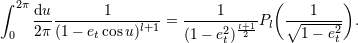 |
|
| 77 | The tetrad is orthonormal in the sense that 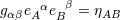 , where , where  denotes a Minkowski
metric. The indices denotes a Minkowski
metric. The indices  are the internal Lorentz indices, while as usual are the internal Lorentz indices, while as usual 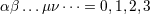 are the
space-time covariant indices. The inverse dual tetrad are the
space-time covariant indices. The inverse dual tetrad 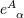 , defined by , defined by 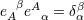 , satisfies , satisfies 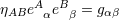 . We have
also the completeness relation . We have
also the completeness relation 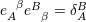 . . |
|
| 78 | Our conventions for the Riemann tensor 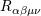 follow those of MTW [319]. follow those of MTW [319]. |
|
| 79 | The four-dimensional Levi-Civita tensor is defined by 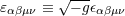 and and 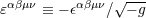 ; here ; here
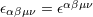 denotes the completely anti-symmetric Levi-Civita symbol such that denotes the completely anti-symmetric Levi-Civita symbol such that 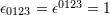 . For convenience in
this section we pose . For convenience in
this section we pose  . . |
|
| 80 | Because of this choice, it is better to consider that the tetrad is not the same as the one we originally employed to construct the action (369*). | |
| 81 | Beware that here we employ the usual slight ambiguity in the notation when using the same carrier letter 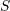 to denote
the tetrad components (384*) and the original spin covector. Thus, to denote
the tetrad components (384*) and the original spin covector. Thus, 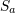 should not be confused with the spatial components should not be confused with the spatial components
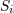 (with (with 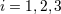 ) of the covariant vector ) of the covariant vector  . . |
|
| 82 | Notation adopted in Ref. [271]; the inverse formulas read
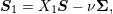 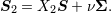 |
|
| 83 | Note that the individual particle’s positions 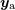 in the frame of the center-of-mass (defined by the cancellation of the
center-of-mass integral of motion: in the frame of the center-of-mass (defined by the cancellation of the
center-of-mass integral of motion: 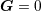 ) are related to the relative position and velocity ) are related to the relative position and velocity 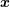 and and  by some expressions
similar to Eqs. (224) but containing spin effects starting at order 1.5PN. by some expressions
similar to Eqs. (224) but containing spin effects starting at order 1.5PN. |
|
| 84 | Beware of our inevitably slightly confusing notation: 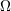 is the binary’s orbital frequency and is the binary’s orbital frequency and 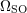 refers to the
spin-orbit terms therein; refers to the
spin-orbit terms therein; 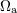 is the precession frequency of the is the precession frequency of the  -th spin while -th spin while 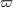 is the precession frequency of the
orbital plane; and is the precession frequency of the
orbital plane; and 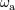 defined earlier in Eqs. (244*) and (284) is the rotation frequency of the defined earlier in Eqs. (244*) and (284) is the rotation frequency of the  -th black hole. Such
different notions nicely mix up in the first law of spinning binary black holes in Section 8.3; see Eq. (282*) and the corotation
condition (285*). -th black hole. Such
different notions nicely mix up in the first law of spinning binary black holes in Section 8.3; see Eq. (282*) and the corotation
condition (285*). |
|
| 85 | Recall from Eq. (366*) that in our convention the spins have the dimension of an angular momentum times
 . . |
|
| 86 | In this section we can neglect the gauge multipole moments 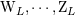 . . |
|
| 87 | Notice that the spin-orbit contributions due to the absorption by the black-hole horizons have to be added to this post-Newtonian result [349, 392, 5, 125]. |
