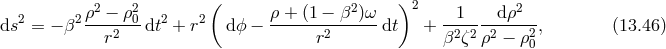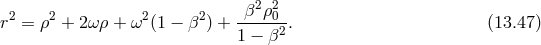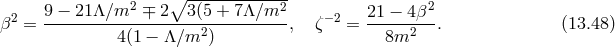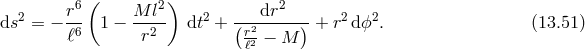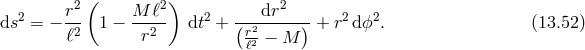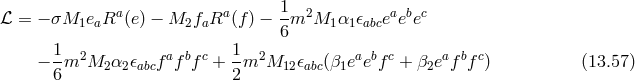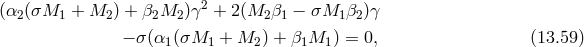13 New Massive Gravity
13.1 Formulation
Independently of the formal development of massive gravity in four dimensions described above, there has been interest in constructing a purely three dimensional theory of massive gravity. Three dimensions are special for the following reason: for a massless graviton in three dimensions there are no propagating degrees of freedom. This follows simply by counting, a symmetric tensor in three dimensions has six components. A massless graviton must admit a diffeomorphism symmetry which renders three of the degrees of freedom pure gauge, and the remaining three are non-dynamical due to the associated first class constraints. On the contrary, a massive graviton in three dimensions has the same number of degrees of freedom as a massless graviton in four dimensions, namely two. Combining these two facts together, in three dimensions it should be possible to construct a diffeomorphism invariant theory of massive gravity. The usual massless graviton implied by diffeomorphism invariance is absent and only the massive degree of freedom remains.
A diffeomorphism and parity invariant theory in three dimensions was given in [66] and referred to as ‘new massive gravity’ (NMG). In its original formulation the action is taken to be
where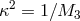 defines the three dimensional Planck mass,
defines the three dimensional Planck mass, 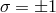 and
and 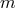 is the mass of the
graviton. In this form the action is manifestly diffeomorphism invariant and constructed entirely out of the
metric
is the mass of the
graviton. In this form the action is manifestly diffeomorphism invariant and constructed entirely out of the
metric 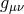 . However, to see that it really describes a massive graviton, it is helpful to introduce an
auxiliary field
. However, to see that it really describes a massive graviton, it is helpful to introduce an
auxiliary field 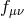 which, as we will see below, also admits an interpretation as a metric, to give a
quasi-bi-gravity formulation
The kinetic term for
which, as we will see below, also admits an interpretation as a metric, to give a
quasi-bi-gravity formulation
The kinetic term for 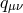 appears from the mixing with
appears from the mixing with 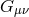 . Although this is not a true bi-gravity
theory, since there is no direct Einstein–Hilbert term for
. Although this is not a true bi-gravity
theory, since there is no direct Einstein–Hilbert term for 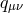 , we shall see below that it is a well-defined
decoupling limit of a bi-gravity theory, and for this reason it makes sense to think of
, we shall see below that it is a well-defined
decoupling limit of a bi-gravity theory, and for this reason it makes sense to think of  as effectively a
metric degree of freedom. In this form, we see that the special form of
as effectively a
metric degree of freedom. In this form, we see that the special form of 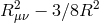 was
designed so that
was
designed so that 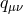 has the Fierz–Pauli mass term. It is now straightforward to see that this
corresponds to a theory of massive gravity by perturbing around Minkowski spacetime. Defining
and perturbing to quadratic order in
has the Fierz–Pauli mass term. It is now straightforward to see that this
corresponds to a theory of massive gravity by perturbing around Minkowski spacetime. Defining
and perturbing to quadratic order in  and
and 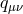 we have
Finally, diagonalizing as
we have
Finally, diagonalizing as 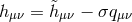 we obtain
which is manifestly a decoupled massless graviton and massive graviton. Crucially, however, we see that the
kinetic terms of each have the opposite sign. Since only the degrees of freedom of the massive graviton
we obtain
which is manifestly a decoupled massless graviton and massive graviton. Crucially, however, we see that the
kinetic terms of each have the opposite sign. Since only the degrees of freedom of the massive graviton 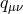 are propagating, unitarity when coupled to other sources forces us to choose
are propagating, unitarity when coupled to other sources forces us to choose 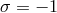 . The apparently
ghostly massless graviton does not lead to any unitarity violation, at least in perturbation theory, as there is
no massless pole in the propagator. The stability of the vacua was further shown in different gauges in
Ref. [252].
. The apparently
ghostly massless graviton does not lead to any unitarity violation, at least in perturbation theory, as there is
no massless pole in the propagator. The stability of the vacua was further shown in different gauges in
Ref. [252].
13.2 Absence of Boulware–Deser ghost
The auxiliary field formulation of new massive gravity is also useful for understanding the absence of the
BD ghost [141*]. Setting  as imposed previously and working with the formulation (13.2*), we can
introduce new vector and scalar degrees of freedom as follows
as imposed previously and working with the formulation (13.2*), we can
introduce new vector and scalar degrees of freedom as follows
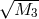 and
and 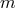 are chosen for canonical normalization.
are chosen for canonical normalization. 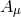 represents the helicity-1
mode which carries 1 degree of freedom and
represents the helicity-1
mode which carries 1 degree of freedom and 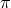 the helicity-0 mode that carries 1 degree freedom. These
two modes carries all the dynamical fields.
the helicity-0 mode that carries 1 degree freedom. These
two modes carries all the dynamical fields.
Introducing new fields in this way also introduced new symmetries. Specifically there is a 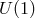 symmetry
symmetry
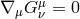 we obtain
Although this action contains apparently higher order terms due to its dependence on
we obtain
Although this action contains apparently higher order terms due to its dependence on 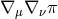 , this
dependence is Galileon-like in that the equations of motion for all fields are second order. For instance the
naively dangerous combination
is up to a boundary term equivalent to
, this
dependence is Galileon-like in that the equations of motion for all fields are second order. For instance the
naively dangerous combination
is up to a boundary term equivalent to 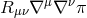 . In [141*] it is shown that the resulting equations of
motion of all fields are second order due to these special Fierz–Pauli combinations.
. In [141*] it is shown that the resulting equations of
motion of all fields are second order due to these special Fierz–Pauli combinations.
As a result of the introduction of the new gauge symmetries, we straightforwardly count the number of
non-perturbative degrees of freedom. The total number of fields are 16: six from 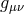 , six from
, six from  , three
from
, three
from 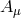 and one from
and one from 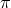 . The total number of gauge symmetries are 7: three from diffeomorphisms,
three from linear diffeomorphisms and one from the
. The total number of gauge symmetries are 7: three from diffeomorphisms,
three from linear diffeomorphisms and one from the 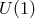 . Thus, the total number of degrees of freedom
are
. Thus, the total number of degrees of freedom
are 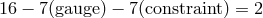 which agrees with the linearized analysis. An independent
argument leading to the same result is given in [317] where NMG including its topologically massive
extension (see below) are presented in Hamiltonian form using Einstein–Cartan language (see
also [176]).
which agrees with the linearized analysis. An independent
argument leading to the same result is given in [317] where NMG including its topologically massive
extension (see below) are presented in Hamiltonian form using Einstein–Cartan language (see
also [176]).
13.3 Decoupling limit of new massive gravity
The formalism of Section 13.2 is also useful for deriving the decoupling limit of NMG which as in the higher dimensional case, determines the leading interactions for the helicity-0 mode. The decoupling limit [141] is defined as the limit
As usual the metric is scaled as and in the action the normalizations have been chosen so that we keep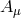 and
and 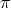 fixed in the limit. We readily find
where all raising and lowering is understood with respect to the 3 dimensional Minkowski metric.
Performing the field redefinition
fixed in the limit. We readily find
where all raising and lowering is understood with respect to the 3 dimensional Minkowski metric.
Performing the field redefinition 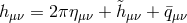 we finally obtain
Thus, we see that in the decoupling limit, NMG becomes equivalent to two massless gravitons which have
no degrees of freedom, one massless spin-1 particle which has one degree of freedom, and one scalar
we finally obtain
Thus, we see that in the decoupling limit, NMG becomes equivalent to two massless gravitons which have
no degrees of freedom, one massless spin-1 particle which has one degree of freedom, and one scalar 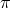 which has a cubic Galileon interaction. This confirms that the strong coupling scale for NMG is
which has a cubic Galileon interaction. This confirms that the strong coupling scale for NMG is
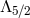 .
.
The decoupling limit clarifies one crucial aspect of NMG. It has been suggested that NMG could be
power counting renormalizable following previous arguments for topological massive gravity [196] due to the
softer nature of divergences in three-dimensional and the existence of a dimensionless combination of the
Planck mass and the graviton mass. This is in fact clearly not the case since the above cubic interaction is a
non-renormalizable operator and dominates the Feynman diagrams leading to perturbative
unitarity violation at the strong coupling scale 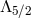 (see Section 10.5 for further discussion on
the distinction between the breakdown of perturbative unitarity and the breakdown of the
theory).
(see Section 10.5 for further discussion on
the distinction between the breakdown of perturbative unitarity and the breakdown of the
theory).
13.4 Connection with bi-gravity
The existence of the NMG theory at first sight appears to be something of an anomaly that cannot be
reproduced in higher dimensions. There also does not at first sight seem to be any obvious connection with
the diffeomorphism breaking ghost-free massive gravity model (or dRGT) and multi-gravity extensions.
However, in [425*] it was shown that NMG, and certain extensions to it, could all be obtained as scaling
limits of the same 3-dimensional bi-gravity models that are consistent with ghost-free massive
gravity in a different decoupling limit. As we already mentioned, the key to seeing this is the
auxiliary formulation where the tensor  is related to the missing extra metric of the bi-gravity
theory.
is related to the missing extra metric of the bi-gravity
theory.
Starting with the 3-dimensional version of bi-gravity [293] in the form
where the bi-gravity potential takes the standard form in terms of characteristic polynomials similarly as in (6.4*) and is given in (6.7*) in terms of the two dynamical metrics
is given in (6.7*) in terms of the two dynamical metrics 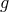 and
and 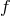 . The scale
. The scale 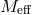 is defined as
is defined as
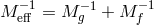 . The idea is to define a scaling limit [425*] as follows
keeping
. The idea is to define a scaling limit [425*] as follows
keeping  fixed and keeping
fixed and keeping 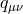 fixed in the definition
Since
fixed in the definition
Since  , then we have in the limit
which prompts the definition of a new set of coefficients
so that
Since this theory is obtained as a scaling limit of the ghost-free bi-gravity action, it is guaranteed to be free
from the BD ghost. We see that in the case
, then we have in the limit
which prompts the definition of a new set of coefficients
so that
Since this theory is obtained as a scaling limit of the ghost-free bi-gravity action, it is guaranteed to be free
from the BD ghost. We see that in the case 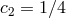 ,
,  we obtain the auxiliary field
formulation of NMG, justifying the connection between the auxiliary field
we obtain the auxiliary field
formulation of NMG, justifying the connection between the auxiliary field 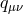 and the bi-gravity metric
and the bi-gravity metric
 .
.
13.5 3D massive gravity extensions
The generic form of the auxiliary field formulation of NMG derived above [425]
demonstrates that there exists a two parameter family extensions of NMG determined by nonzero coefficients for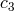 and
and 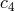 . The purely metric formulation for the generic case can be determined by
integrating out the auxiliary field
. The purely metric formulation for the generic case can be determined by
integrating out the auxiliary field 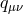 . The equation of motion for
. The equation of motion for 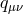 is given symbolically
This is a quadratic equation for the tensor
is given symbolically
This is a quadratic equation for the tensor 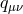 . Together, these two additional degrees of freedom give the
cubic curvature [447] and Born–Infeld extension NMG [279*]. Although additional higher derivative
corrections have been proposed based on consistency with the holographic c-theorem [424], the above
connection suggests that Eq. (13.23*) is the most general set of interactions allowed in NMG which are free
from the BD ghost.
. Together, these two additional degrees of freedom give the
cubic curvature [447] and Born–Infeld extension NMG [279*]. Although additional higher derivative
corrections have been proposed based on consistency with the holographic c-theorem [424], the above
connection suggests that Eq. (13.23*) is the most general set of interactions allowed in NMG which are free
from the BD ghost.
In the specific case of the Born–Infeld extension [279] the action is
It is straightforward to show that on expanding the square root to second order in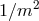 we recover the
original NMG action. The specific case of the Born–Infeld extension of NMG, also has a surprising role as a
counterterm in the AdS4 holographic renormalization group [329]. The significance of this relation is
unclear at present.
we recover the
original NMG action. The specific case of the Born–Infeld extension of NMG, also has a surprising role as a
counterterm in the AdS4 holographic renormalization group [329]. The significance of this relation is
unclear at present.
13.6 Other 3D theories
13.6.1 Topological massive gravity
In four dimensions, the massive spin-2 representations of the Poincaré group must come in positive and negative helicity pairs. By contrast, in three dimensions the positive and negative helicity states are completely independent. Thus, while a parity preserving theory of massive gravity in three dimensions will contain two propagating degrees of freedom, it seems possible in principle for there to exist an interacting theory for one of the helicity modes alone. What is certainly possible is that one can give different interactions to the two helicity modes. Such a theory necessarily breaks parity, and was found in [180, 179]. This theory is known as ‘topologically massive gravity’ (TMG) and is described by the Einstein–Hilbert action, with cosmological constant, supplemented by a term constructed entirely out of the connection (hence the name topological)
The new interaction is a gravitational Chern–Simons term and is responsible for the parity breaking. More generally, this action may be supplemented to the NMG Lagrangian interactions and so the TMG can be viewed as a special case of the full extended parity violating NMG.The equations of motion for topologically massive gravity take the form
where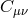 is the Cotton tensor which is given by
Einstein metrics for which
is the Cotton tensor which is given by
Einstein metrics for which 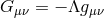 remain as a subspace of general set of vacuum solutions. In the
case where the cosmological constant is negative
remain as a subspace of general set of vacuum solutions. In the
case where the cosmological constant is negative  we can use the correspondence of Brown and
Henneaux [78] to map the theory of gravity on an asymptotically AdS3 space to a 2D CFT living at the
boundary.
we can use the correspondence of Brown and
Henneaux [78] to map the theory of gravity on an asymptotically AdS3 space to a 2D CFT living at the
boundary.
The AdS/CFT in the context of topological massive gravity was also studied in Ref. [449*].
13.6.2 Supergravity extensions
As with any gravitational theory, it is natural to ask whether extensions exist which exhibit local
supersymmetry, i.e., supergravity. A supersymmetric extension to topologically massive gravity was given
in [182]. An 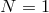 supergravity extension of NMG including the topologically massive gravity terms was
given in [21*] and further generalized in [67*]. The construction requires the introduction of an ‘auxiliary’
bosonic scalar field
supergravity extension of NMG including the topologically massive gravity terms was
given in [21*] and further generalized in [67*]. The construction requires the introduction of an ‘auxiliary’
bosonic scalar field 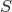 so that the form of the action is
so that the form of the action is
Moreover, 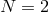 supergravity extensions of TMG were recently constructed in Ref. [370] and its
supergravity extensions of TMG were recently constructed in Ref. [370] and its
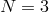 and
and 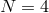 supergravity extensions in Ref. [371].
supergravity extensions in Ref. [371].
13.6.3 Critical gravity
Finally, let us comment on a special case of three dimensional gravity known as log gravity [65] or critical gravity in analogy with the general dimension case [384, 183, 16]. For a special choice of parameters of the theory, there is a degeneracy in the equations of motion for the two degrees of freedom leading to the fact that one of the modes of the theory becomes a ‘logarithmic’ mode.
Indeed, at the special point 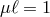 , (where
, (where 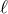 is the AdS length scale,
is the AdS length scale, 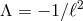 ), known as the
‘chiral point’ the left-moving (in the language of the boundary CFT) excitations of the theory
become pure gauge and it has been argued that the theory then becomes purely an interacting
theory for the right moving graviton [93*]. In Ref. [377] it was earlier argued that there was no
massive graviton excitations at the critical point
), known as the
‘chiral point’ the left-moving (in the language of the boundary CFT) excitations of the theory
become pure gauge and it has been argued that the theory then becomes purely an interacting
theory for the right moving graviton [93*]. In Ref. [377] it was earlier argued that there was no
massive graviton excitations at the critical point 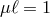 , however Ref. [93] found one massive
graviton excitation for every finite and non-zero value of
, however Ref. [93] found one massive
graviton excitation for every finite and non-zero value of 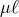 , including at the critical point
, including at the critical point
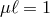 .
.
This case was further analyzed in [273*], see also Ref. [274*] for a recent review. It was shown that the degeneration of the massive graviton mode with the left moving boundary graviton leads to logarithmic excitations.
To be more precise, starting with the auxiliary formulation of NMG with a cosmological constant 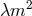
 in
in
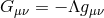 is not the same as
is not the same as 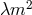 . The relation between the two is set by the vacuum equations to
be
which generically has two solutions. Perturbing the action to quadratic order around this vacuum solution
we have
where
and
where we raise and lower the indices with respect to the background AdS metric
. The relation between the two is set by the vacuum equations to
be
which generically has two solutions. Perturbing the action to quadratic order around this vacuum solution
we have
where
and
where we raise and lower the indices with respect to the background AdS metric 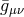 .
.
As usual, it is apparent that this theory describes one massless graviton (with no propagating degrees of
freedom) and one massive one whose mass is given by 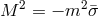 . However, by choosing
. However, by choosing 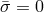 the
massive mode becomes degenerate with the existing massless one.
the
massive mode becomes degenerate with the existing massless one.
In this case, the action is
and varying with respect to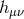 and
and 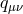 we obtain the equations of motion
Choosing the gauge
we obtain the equations of motion
Choosing the gauge 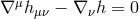 , the equations of motion imply
, the equations of motion imply 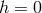 and the resulting equation
of motion for
and the resulting equation
of motion for 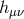 takes the form
It is this factorization of the equations of motion into a square of an operator that is characteristic of the
critical/log gravity theories. Although the equation of motion is solved by the usual massless models for
which
takes the form
It is this factorization of the equations of motion into a square of an operator that is characteristic of the
critical/log gravity theories. Although the equation of motion is solved by the usual massless models for
which ![[□ − 2Λ]h μν = 0](article2617x.gif) , there are additional logarithmic modes which do not solve this equation but do
solve Eq. (13.45*). These are so-called because they behave logarithmically in
, there are additional logarithmic modes which do not solve this equation but do
solve Eq. (13.45*). These are so-called because they behave logarithmically in 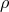 asymptotically when the
AdS metric is put in the form
asymptotically when the
AdS metric is put in the form 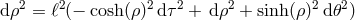 . The presence of these log
modes was shown to remain beyond the linear regime, see Ref. [271].
. The presence of these log
modes was shown to remain beyond the linear regime, see Ref. [271].
Based on this result as well as on the finiteness and conservation of the stress tensor and on the emergence of a Jordan cell structure in the Hamiltonian, the correspondence to a logarithmic CFT was conjectured in Ref. [273], where the to be dual log CFTs representations have degeneracies in the spectrum of scaling dimensions.
Strong indications for this correspondence appeared in many different ways. First, consistent boundary conditions which allow the log modes were provided in Ref. [272], were it was shown that in addition to the Brown–Henneaux boundary conditions one could also consider more general ones. These boundary conditions were further explored in [305, 397], where it was shown that the stress-energy tensor for these boundary conditions are finite and not chiral, giving another indication that the theory could be dual to a logarithmic CFT.
Then specific correlator functions were computed and compared. Ref. [449] checked the 2-point correlators and Ref. [275] the 3-point ones. A similar analysis was also performed within the context of NMG in Ref. [270] where the 2-point correlators were computed at the chiral point and shown to behave as those of a logarithmic CFT.
Further checks for this AdS/log CFT include the 1-loop partition function as computed in Ref. [241]. See also Ref. [274] for a review of other checks.
It has been shown, however, that ultimately these theories are non-unitary due to the fact that there is a non-zero inner product between the log modes and the normal models and the inability to construct a positive definite norm on the Hilbert space [432].
13.7 Black holes and other exact solutions
A great deal of physics can be learned from studying exact solutions, in particular those corresponding to black hole geometries. Black holes are also important probes of the non-perturbative aspects of gravitational theories. We briefly review here the types of exact solutions obtained in the literature.
In the case of topologically massive gravity, a one-parameter family of extensions to the BTZ black hole have been obtained in [245]. In the case of NMG as well as the usual BTZ black holes obtained in the presence of a negative cosmological constant there are in a addition a class of warped AdS3 black holes [102] whose metric takes the form
where the radial coordinate is given by
and the parameters
is given by
and the parameters  and
and 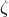 are determined in terms of the graviton mass
are determined in terms of the graviton mass 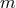 and the cosmological
constant
and the cosmological
constant 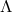 by
This metric exhibits two horizons at
by
This metric exhibits two horizons at 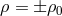 , if
, if 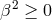 and
and 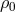 is real. Absence of closed
timelike curves requires that
is real. Absence of closed
timelike curves requires that 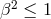 . This puts the allowed range on the values of
. This puts the allowed range on the values of 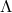 to be
AdS waves, extensions of plane (pp) waves anti-de Sitter spacetime have been considered in [33]. Further
work on extensions to black hole solutions, including charged black hole solutions can be found
in [418, 101, 253, 5, 6, 372, 427, 250]. We note in particular the existence of a class of Lifshitz black
holes [32*] that exhibit the Lifshitz anisotropic scale symmetry
where
to be
AdS waves, extensions of plane (pp) waves anti-de Sitter spacetime have been considered in [33]. Further
work on extensions to black hole solutions, including charged black hole solutions can be found
in [418, 101, 253, 5, 6, 372, 427, 250]. We note in particular the existence of a class of Lifshitz black
holes [32*] that exhibit the Lifshitz anisotropic scale symmetry
where  is the dynamical critical exponent. As an example for
is the dynamical critical exponent. As an example for 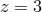 the following Lifshitz black hole
can be found [32]
This metric has a curvature singularity at
the following Lifshitz black hole
can be found [32]
This metric has a curvature singularity at 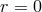 and a horizon at
and a horizon at 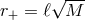 . The Lifshitz symmetry is
preserved if we scale
. The Lifshitz symmetry is
preserved if we scale 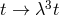 ,
, 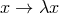 ,
,  and in addition we scale the black hole mass as
and in addition we scale the black hole mass as
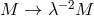 . The metric should be contrasted with the normal BTZ black hole which corresponds to
. The metric should be contrasted with the normal BTZ black hole which corresponds to
 Exact solutions for charged black holes were also derived in Ref. [249] and an exact, non-stationary solution
of TMG and NMG with the asymptotic charges of a BTZ black hole was find in [227]. This exact solution
was shown to admit a timelike singularity. Other exact asymptotically AdS-like solutions were found in
Ref. [251].
Exact solutions for charged black holes were also derived in Ref. [249] and an exact, non-stationary solution
of TMG and NMG with the asymptotic charges of a BTZ black hole was find in [227]. This exact solution
was shown to admit a timelike singularity. Other exact asymptotically AdS-like solutions were found in
Ref. [251].
13.8 New massive gravity holography
One of the most interesting avenues of exploration for NMG has been in the context of Maldacena’s AdS/CFT correspondence [396]. According to this correspondence, NMG with a cosmological constant chosen so that there are asymptotically anti-de Sitter solutions is dual to a conformal field theory (CFT). This has been considered in [67*, 381, 380] where it was found that the requirements of bulk unitarity actually lead to a negative central charge.
The argument for this proceeds from the identification of the central charge of the dual two dimensional field theory with the entropy of a black hole in the bulk using Cardy’s formula. The entropy of the black hole is given by [368]
where is the 3-dimensional Newton constant and
is the 3-dimensional Newton constant and 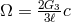 where
where 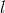 is the AdS radius and
is the AdS radius and  is
the central charge. This formula is such that
is
the central charge. This formula is such that 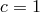 for pure Einstein–Hilbert gravity with a negative
cosmological constant.
for pure Einstein–Hilbert gravity with a negative
cosmological constant.
A universal formula for this central charge has been obtained as is given by
This result essentially follows from using the Wald entropy formula [480] for a higher derivative gravity theory and identifying this with the central change through the Cardy formula. Applying this argument for new massive gravity we obtain [67] Since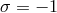 is required for bulk unitarity, we must choose
is required for bulk unitarity, we must choose 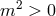 to have a chance of
getting
to have a chance of
getting  positive. Then we are led to conclude that the central charge is only positive if
However, unitarity in the bulk requires
positive. Then we are led to conclude that the central charge is only positive if
However, unitarity in the bulk requires 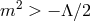 and this excludes this possibility. We are thus led to
conclude that NMG cannot be unitary both in the bulk and in the dual CFT. This failure to maintain both
bulk and boundary unitarity can be resolved by a modification of NMG to a full bi-gravity model, namely
Zwei-Dreibein gravity to which we turn next.
and this excludes this possibility. We are thus led to
conclude that NMG cannot be unitary both in the bulk and in the dual CFT. This failure to maintain both
bulk and boundary unitarity can be resolved by a modification of NMG to a full bi-gravity model, namely
Zwei-Dreibein gravity to which we turn next.
13.9 Zwei-dreibein gravity
As we have seen, there is a conflict in NMG between unitarity in the bulk, i.e., the requirement that the massive gravitons are not ghosts, and unitarity in dual CFT as required by the positivity of the central charge. This conflict may be resolved, however, by replacing NMG with the 3-dimensional bi-gravity extension of ghost-free massive gravity that we have already discussed. In particular, if we work in the Einstein–Cartan formulation in three dimensions, then the metric is replaced by a ‘dreibein’ and since this is a bi-gravity model, we need two ‘dreibeins’. This gives us the Zwei-dreibein gravity [63*].
In the notation of [63*] the Lagrangian is given by
where we have suppressed the wedge products ,
, 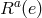 is Lorentz vector valued curvature
two-form for the spin-connection associated with the dreibein
is Lorentz vector valued curvature
two-form for the spin-connection associated with the dreibein  and
and 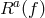 that associated with
the dreibein
that associated with
the dreibein  . Since we are in three dimensions, the spin-connection can be written as a
Lorentz vector dualizing with the Levi-Civita symbol
. Since we are in three dimensions, the spin-connection can be written as a
Lorentz vector dualizing with the Levi-Civita symbol 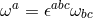 . This is nothing other
than the vierbein representation of bi-gravity with the usual ghost-free (dRGT) mass terms.
As we have already discussed, NMG and its various extensions arise in appropriate scaling
limits.
. This is nothing other
than the vierbein representation of bi-gravity with the usual ghost-free (dRGT) mass terms.
As we have already discussed, NMG and its various extensions arise in appropriate scaling
limits.
A computation of the central charge following the same procedure was given in [63*] with the result that
Defining the parameter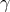 via the relation
then bulk unitarity requires
via the relation
then bulk unitarity requires  . In order to have
. In order to have 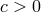 we thus need
we thus need 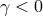 which in
turn implies
which in
turn implies 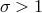 (since
(since 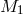 and
and 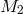 are defined as positive). The absence of tachyons
in the AdS vacuum requires
are defined as positive). The absence of tachyons
in the AdS vacuum requires 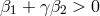 , and this assumes a real solution for
, and this assumes a real solution for 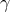 for a
negative
for a
negative 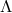 . There are an open set of such solutions to these conditions, which shows that the
conditions for unitarity are not finely tuned. For example in [63] it is shown that there is an open
set of solutions which are close to the special case
. There are an open set of such solutions to these conditions, which shows that the
conditions for unitarity are not finely tuned. For example in [63] it is shown that there is an open
set of solutions which are close to the special case 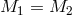 ,
, 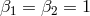 ,
, 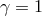 and
and
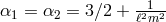 . This result is not in contradiction with the scaling limit that reproduces NMG,
because this scaling limit requires the choice
. This result is not in contradiction with the scaling limit that reproduces NMG,
because this scaling limit requires the choice 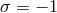 which is in contradiction with positive central
charge.
which is in contradiction with positive central
charge.
These results potentially have an impact on the higher dimensional case. We see that in three dimensions we potentially have a diffeomorphism invariant theory of massive gravity (i.e., bi-gravity) which at least for AdS solutions exhibits unitarity both in the bulk and in the boundary CFT for a finite range of parameters in the theory. However, these bi-gravity models are easily extended into all dimensions as we have already discussed and it is similarly easy to find AdS solutions which exhibit bulk unitarity. It would be extremely interesting to see if the associated dual CFTs are also unitary thus providing a potential holographic description of generalized theories of massive gravity.

 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
 )
)![[ ( ) ] 1 ∫ 3 √ --- 1 μν 3 2 SNMG = -2- d x − g σR + --2 RμνR − -R , (13.1 ) κ m 8](article2496x.gif)
![[ ] ∫ 3 √ --- μν 1 2 μν 2 SNMG = M3 d x − g σR − q G μν − -m (qμνq − q ) . (13.2 ) 4](article2502x.gif)

![∫ [ ] 3 σ μν αβ μν αβ 1 2 μν 2 S2 = M3 d x − --h ˆℰμν hαβ − q ˆℰμν h αβ −-m (qμνq − q ) . (13.4 ) 2 4](article2512x.gif)
![∫ [ ] 3 σ-&tidle;μν ˆα β&tidle; σ- μν ˆαβ 1- 2 μν 2 S2 = M3 d x − 2 h ℰμν hαβ + 2 q ℰμν qαβ − 4 m (qμνq − q ) , (13.5 )](article2514x.gif)
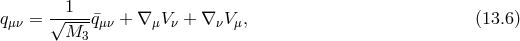


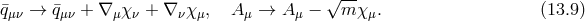
![[ ∫ √--- ∘ ---- SNMG = d3x − g − M3R − M3 q¯μνG μν (13.10 ) 1 ( 2 − -- (m ¯qμν + ∇μA ν + ∇ νAμ + --∇ μ∇ νπ)2 4 ] m 2 2) − (m ¯q + 2∇A + m- □π ) .](article2528x.gif)

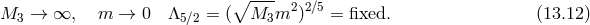

![[ ∫ √--- ∘ ---- SNMG = d3x − g − M3R − M3 q¯μνG μν (13.14 ) 1 ( 2 − -- (m ¯qμν + ∇μA ν + ∇ νAμ + --∇ μ∇ νπ)2 4 ] m 2 2) − (m ¯q + 2∇A + m- □π ) ,](article2540x.gif)
![∫ [ S = d3x + 1h μν ˆℰαβh − q¯μν ˆℰαβh − ¯qμν(∂ ∂ π − η □ π) dec 2 μν αβ μν αβ μ ν μν ] 1 μν 1 μν αβ 2 − 4-FμνF + -5∕2ℰˆαβ h (∂μπ∂ νπ − ημν(∂π) ) , (13.15 ) Λ5∕2](article2543x.gif)
![[ ∫ 1 1 Sdec = d3x + --&tidle;hμν ˆℰαμβν &tidle;hαβ −-¯qμνℰˆαμβν ¯qαβ 2 2 ] − 1F F μν − 1(∂ π)2 − --1--(∂π )2□π . (13.16 ) 4 μν 2 2Λ5∕2 5∕2](article2545x.gif)
![∫ [ ] 3 Mg √ --- Mf ∘ ---- 2 S = d x -2-- − gR [g ] +-2-- − fR [f ] − m 𝒰 [g,f ] , (13.17 )](article2550x.gif)
![3 𝒰 [g,f] = − Me-ff∑ α ℒ (𝒦 ), (13.18 ) 4 n n n=0](article2551x.gif)


![∫ [ 3 ( ) ] 3 M3-√ --- M3--μν m2Me--ff∑ n -M3- n S = d x − 2 − gR[g] − 2 q G μν(g) + 4 αn(− 1) M ℒn (q) n=0 f](article2562x.gif)

![[ ] ∫ √ --- ∑3 S = M3 d3x − − gR [g] − qμνG μν(g) − m2 cnℒn(q) . (13.22 ) n=0](article2564x.gif)
![∫ [ 3 ] 3 √ --- μν 2 ∑ S = M3 d x − − gR [g ] − q G μν(g) − m cnℒn (q) , (13.23 ) n=0](article2569x.gif)
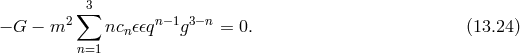
![∫ [ ∘ --------------------] 2 3 √ --- -1- SB.I = 4m M3 d x − g − − det [gμν − m2 G μν] . (13.25 )](article2576x.gif)
![∫ [ ] M3 3 √ --- 1 λμν ρ σ 2 σ τ S = ---- d x − g(R − 2Λ ) + --𝜖 Γ λσ ∂μ Γρν + -Γ μτΓ νρ . (13.26 ) 2 4μ 3](article2578x.gif)


![∫ [ ] 1 3 √ --- 1 1 1 1 S = -2- d x − g M ℒC + σℒE.H. + --2 ℒK + ---2ℒR2 + --2ℒS4 + --ℒS3 κ ∫ m 8&tidle;m ˆm ˆμ + d3x 1ℒ , (13.29 ) μ top](article2586x.gif)
![ℒC = S + fermions (13.30 ) ℒE.H.= R − 2S2 + fermions (13.31 ) 1 3 ℒK = K − --S2R − -S4 + fermions (13.32 ) 2[ 2 ] 2 9- 2 1- 2 ℒR2 = − 16 (∂S ) − 4(S + 6 R) + fermions (13.33 ) 3 ℒS4 = S4 + --RS2 + fermions (13.34 ) 10 ℒ 3 = S3 + 1RS + fermions (13.35 ) S 2 1 ρ [ 2 ] ℒtop = --𝜖λμνΓ λσ ∂ μΓ σρν +-Γ σμτΓ τνρ + fermions. (13.36 ) 4 3](article2587x.gif)
![∫ √ --- [ 1 ] SNMG = M3 d3x − g σR − 2λm2 − qμνG μν − -m2 (qμνqμν − q2) , (13.37 ) 4](article2598x.gif)

![∫ [ ] 3 ¯σ μν μν 1 2 μν 2 S2 = M3 d x − 2h 𝒢μν − q 𝒢μν − 4m (qμνq − q ) . (13.39 )](article2603x.gif)
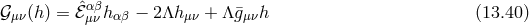

![∫ [ ] 3 μν 1 2 μν 2 S2 = M3 d x − q 𝒢μν − 4-m (qμνq − q ) , (13.42 )](article2609x.gif)

![[□ − 2 Λ]2hμν = 0. (13.45 )](article2616x.gif)