6 Massive, Bi- and Multi-Gravity Formulation: A Summary
The previous ‘deconstruction’ framework gave a intuitive argument for the emergence of a potential of the form (6.3*) (or (6.1*) in the vielbein language) and its bi- and multi-metric generalizations. In deconstruction or Kaluza–Klein decomposition a certain type of interaction arises naturally and we have seen that the whole spectrum of allowed potentials (or interactions) could be generated by extending the deconstruction procedure to a more general notion of derivative or by involving the mixing of more sites in the definition of the derivative along the extra dimensions. We here summarize the most general formulation for the theories of massive gravity about a generic reference metric, bi-gravity and multi-gravity and provide a dictionary between the different languages used in the literature.The general action for ghost-free (or dRGT) massive gravity [144*] in the vielbein language is [95*, 314*] (see however Footnote 13 with respect to Ref. [95*], see also Refs. [502, 410] for earlier work)
with or in the metric language [144*], In what follows we will use the notation for the overall potential of massive gravity so that where![ℒGR [g ]](article881x.gif) is the standard GR Einstein–Hilbert Lagrangian for the dynamical metric
is the standard GR Einstein–Hilbert Lagrangian for the dynamical metric 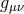 and
and 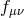 is the reference metric and for bi-gravity,
where both
is the reference metric and for bi-gravity,
where both 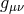 and
and 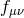 are then dynamical metrics.
are then dynamical metrics.
Both massive gravity and bi-gravity break one copy of diff invariance and so the Stückelberg
fields can be introduced in exactly the same way in both cases ![&tidle; 𝒰[g,f] → 𝒰[g,f]](article887x.gif) where the
Stückelbergized metric
where the
Stückelbergized metric 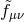 was introduced in (2.75*) (or alternatively
was introduced in (2.75*) (or alternatively ![𝒰 [g,f ] → 𝒰 [&tidle;g,f ]](article889x.gif) ). Thus
bi-gravity is by no means an alternative to introducing the Stückelberg fields as is sometimes
stated.
). Thus
bi-gravity is by no means an alternative to introducing the Stückelberg fields as is sometimes
stated.
In these formulations, 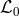 (or the term proportional to
(or the term proportional to 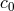 ) correspond to a cosmological
constant,
) correspond to a cosmological
constant, 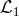 to a tadpole,
to a tadpole, 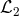 to the mass term and
to the mass term and 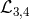 to allowed higher order interactions.
The presence of the tadpole
to allowed higher order interactions.
The presence of the tadpole 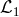 would imply a non-zero vev. The presence of the potentials
would imply a non-zero vev. The presence of the potentials
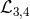 without
without 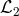 would lead to infinitely strongly coupled degrees of freedom and would
thus be pathological. We recall that
would lead to infinitely strongly coupled degrees of freedom and would
thus be pathological. We recall that ![𝒦 [g,f]](article898x.gif) is given in terms of the metrics
is given in terms of the metrics 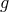 and
and 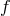 as
as
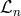 are defined as follows in arbitrary dimensions
are defined as follows in arbitrary dimensions 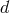 [144*]
with
[144*]
with ![ℒ0 [Q ] = d!](article905x.gif) and
and ![ℒ1[Q ] = (d − 1)![Q]](article906x.gif) or equivalently in four dimensions [292*]
or equivalently in four dimensions [292*]
We have introduced the constant 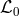 (
(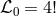 and
and 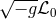 is nothing other than the cosmological
constant) and the tadpole
is nothing other than the cosmological
constant) and the tadpole 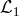 for completeness. Notice however that not all these five Lagrangians are
independent and the tadpole can always be re-expressed in terms of a cosmological constant and the other
potential terms.
for completeness. Notice however that not all these five Lagrangians are
independent and the tadpole can always be re-expressed in terms of a cosmological constant and the other
potential terms.
Alternatively, we may express these scalars as follows [144*]
These are easily generalizable to any number of dimensions, and in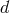 dimensions we find
dimensions we find 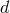 such
independent scalars.
such
independent scalars.
The multi-gravity action is a generalization to multiple interacting spin-2 fields with the same
form for the interactions, and bi-gravity is the special case of two metrics ( ), [314*]
), [314*]
Inverse argument
We could have written this set of interactions in terms of ![𝒦 [f, g]](article918x.gif) rather than
rather than ![𝒦 [g,f]](article919x.gif) ,
,
 implies
implies 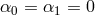 which in turn implies the absence of tadpole and cosmological constant for the other metric
which in turn implies the absence of tadpole and cosmological constant for the other metric 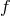 ,
,
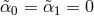 , and thus
, and thus 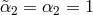 .
.
Alternative variables
Alternatively, another fully equivalent convention has also been used in the literature [292] in terms of
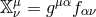 defined in (2.76*),
defined in (2.76*),
 and
or the inverse relation,
so that in order to avoid a tadpole and a cosmological constant we need to set for instance
and
or the inverse relation,
so that in order to avoid a tadpole and a cosmological constant we need to set for instance
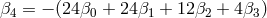 and
and 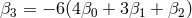 .
.
Expansion about the reference metric
In the vielbein language the mass term is extremely simple, as can be seen in Eq. (6.1*) with  defined
in (2.60*). Back to the metric language, this means that the mass term takes a remarkably simple form when
writing the dynamical metric
defined
in (2.60*). Back to the metric language, this means that the mass term takes a remarkably simple form when
writing the dynamical metric 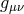 in terms of the reference metric
in terms of the reference metric 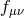 and a difference
and a difference
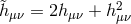 as
as
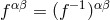 . The mass terms is then expressed as
where the
. The mass terms is then expressed as
where the 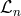 have the same expression as the
have the same expression as the 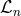 in (6.9*) – (6.13*) so
in (6.9*) – (6.13*) so 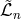 is genuinely
is genuinely 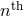 order in
order in
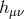 . The expression (6.27*) is thus at most quartic order in
. The expression (6.27*) is thus at most quartic order in 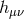 but is valid to all orders in
but is valid to all orders in 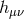 ,
(there is no assumption that
,
(there is no assumption that 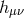 be small). In other words, the mass term (6.27*) is not an expansion in
be small). In other words, the mass term (6.27*) is not an expansion in
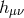 truncated to a finite (quartic) order, but rather a fully equivalent way to rewrite the mass Lagrangian
in terms of the variable
truncated to a finite (quartic) order, but rather a fully equivalent way to rewrite the mass Lagrangian
in terms of the variable 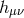 rather than
rather than 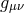 . Of course the kinetic term is intrinsically non-linear and
includes a infinite expansion in
. Of course the kinetic term is intrinsically non-linear and
includes a infinite expansion in 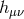 . A generalization of such parameterizations are provided in
[300*].
. A generalization of such parameterizations are provided in
[300*].
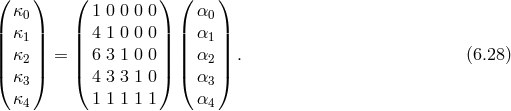
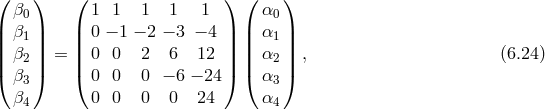
The relation between the coefficients 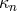 and
and 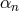 is given by
is given by
The quadratic expansion about a background different from the reference metric was derived in Ref. [278*]. Notice however that even though the mass term may not appear as having an exact Fierz–Pauli structure as shown in [278], it still has the correct structure to avoid any BD ghost, about any background [295*, 294*, 300, 297*].

 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
 )
)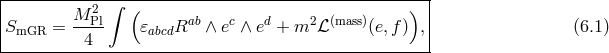
![|------------------[--------------------------------------| ℒ (mass)(e,f) = 𝜀abcd c0ea ∧ eb ∧ ec ∧ ed + c1ea ∧ eb ∧ ec ∧ f d | a b c d a b c d | | +c2e ∧ e ∧ f ∧ f + c3e ∧ f ∧ f ∧ f | (6.2 ) | a b c d] | | +c4f ∧ f ∧ f ∧ f , | -----------------------------------------------------------](article877x.gif)
![|-------------∫-----------(----------4--------------)---| | M-2Pl 4 √ --- m2- ∑ | |SmGR = 2 d x − g R + 2 αn ℒn[𝒦 [g, f]] . | (6.3 ) ------------------------------------n=0-----------------|](article878x.gif)
![2 ∑4 𝒰 = − M-Pl√ −-g αnℒn [𝒦[g,f]] = − ℒ (mass)(e,f), (6.4 ) 4 n=0](article879x.gif)
![ℒmGR = M P2lℒGR [g] − m2 𝒰 [g,f ], (6.5 )](article880x.gif)
![ℒ = M 2ℒ [g] + M 2ℒ [f] − m2 𝒰 [g, f], (6.6 ) bi− gravity Pl GR f GR](article884x.gif)
![|---------------(∘------)-μ-| 𝒦 μν[g,f] = δμν − g−1f ,| (6.7 ) --------------------------ν--](article901x.gif)
![∑n ℒn[Q ] = − (d − n)! (− 1)m-------(n −-1)!------[Qm ]ℒ(nn−m )[Q ], (6.8 ) m=1 (n − m )!(d − n + m )!](article904x.gif)
![μναβ ℒ0 [Q ] = 𝜀 𝜀μναβ ′ (6.9 ) ℒ1 [Q ] = 𝜀μναβ𝜀μ′ναβQ μμ (6.10 ) μναβ μ′ ν′ ℒ2 [Q ] = 𝜀 𝜀μ′ν′αβQ ν Q ν (6.11 ) ℒ3 [Q ] = 𝜀μναβ𝜀μ′ν′α′βQ μν′Q ν′ν Q αα′ (6.12 ) μναβ μ′ ν′ α′ β′ ℒ4 [Q ] = 𝜀 𝜀μ′ν′α′β′Q ν Q ν Qα Q β . (6.13 )](article907x.gif)
![ℒ0[Q ] = 4! (6.14 ) ℒ [Q ] = 3![Q] (6.15 ) 1 2 2 ℒ2[Q ] = 2!([Q ] − [Q ]) (6.16 ) ℒ3[Q ] = ([Q]3 − 3[Q][Q2] + 2[Q3 ]) (6.17 ) 4 2 2 2 2 3 4 ℒ4[Q ] = ([Q] − 6[Q] [Q ] + 3[Q ] + 8[Q ][Q ] − 6[Q ]). (6.18 )](article912x.gif)
![|-------------------------------------------------------------| | M 2 ∑N ∫ ( ) | SN = --Pl 𝜀abcdRab[ej] ∧ ecj ∧ edj + m2N ℒ(mass)(ej,ej+1) , (6.19 ) | 4 j=1 | ---------------------------------------------------------------](article916x.gif)
![|---------------------------(----------------------------------)--| | M 2 ∑N ∫ ∘ ---- m2 ∑4 | |SN = --Pl d4x − gj R[gj] +--N- α (jn)ℒn[𝒦 [gj,gj+1]] .| (6.20 ) | 2 j=1 2 n=0 | ------------------------------------------------------------------](article917x.gif)
![∫ M-2Plm2-- 4 √ --- ∑4 𝒰 = 4 d x − g αn ℒn[𝒦 [g, f]] n=0 M 2m2 ∫ ∘ ---∑4 = --Pl--- d4x − f &tidle;αnℒn [𝒦[f,g]], (6.21 ) 4 n=0](article920x.gif)
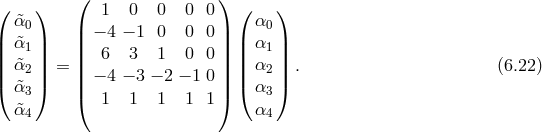
![2 --- ∑4 √ -- 𝒰 = − M-Pl√ − g βn-ℒn [ 𝕏 ], (6.23 ) 4 n=0 n!](article928x.gif)


![M 2 ∘ ---∑ 4 𝒰 = − --Pl − f κnℒn [fμαhα ν], (6.27 ) 4 n=0](article940x.gif)