List of Footnotes
| 1 | In the case of ‘discretization’ or ‘deconstruction’ the higher dimensional approach has been useful only ‘after the fact’. Unlike for DGP, in massive gravity the extra dimension is purely used as a mathematical tool and the formulation of the theory was first performed in four dimensions. In this case massive gravity is not derived per se from the higher-dimensional picture but rather one can see how the structure of general relativity in higher dimensions is tied to that of the mass term. | |
| 2 | The equation of motion with respect to 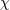 gives gives 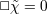 , however this should be viewed as a dynamical relation for , however this should be viewed as a dynamical relation for
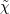 , which should not be plugged back into the action. On the other hand, when deriving the equation of motion with respect
to , which should not be plugged back into the action. On the other hand, when deriving the equation of motion with respect
to 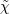 , we obtain a constraint equation for , we obtain a constraint equation for 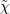 : : 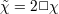 which can be plugged back into the action (and which can be plugged back into the action (and 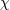 is then
treated as the dynamical field). is then
treated as the dynamical field). |
|
| 3 | This is already a problem at the classical level, well before the notion of particle needs to be defined, since classical
configurations with arbitrarily large 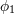 can always be constructed by compensating with a large configuration for can always be constructed by compensating with a large configuration for 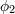 at no
cost of energy (or classical Hamiltonian). at no
cost of energy (or classical Hamiltonian). |
|
| 4 | In this review, the notion of fully non-linear coordinate transformation invariance is equivalent to that of full diffeomorphism invariance or covariance. | |
| 5 | Up to other Lovelock invariants. Note however that 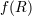 theories are not exceptions, as the kinetic term for the
spin-2 field is still given by theories are not exceptions, as the kinetic term for the
spin-2 field is still given by  . See Section 5.6 for more a more detailed discussion in the case of massive
gravity. . See Section 5.6 for more a more detailed discussion in the case of massive
gravity. |
|
| 6 | Strictly speaking, the notion of spin is only meaningful as a representation of the Lorentz group, thus the theory of massive
spin-2 field is only meaningful when Lorentz invariance is preserved, i.e., when the reference metric is Minkowski. While the
notion of spin can be extended to other maximally symmetric spacetimes such as AdS and dS, it loses its meaning for
non-maximally symmetric reference metrics 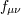 . . |
|
| 7 | This procedure can of course be used for any reference metric, but it fails in identifying the proper physical degrees of freedom when dealing with a general reference metric. See Refs. [145*, 154*] as well as Section 8.3.5 for further discussions on that point. | |
| 8 | In the normal branch of DGP, this brane-bending mode turns out not to be normalizable. The normalizable brane-bending mode which is instead present in the normal branch fully decouples and plays no role. | |
| 9 | Note that in DGP, one could also consider a smooth brane first and the results would remain unchanged. | |
| 10 | The local gauge invariance associated with covariance leads to 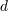 first class constraints which remove first class constraints which remove 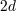 degrees of
freedom, albeit in phase space. For global symmetries such as Lorentz invariance, there is no first-class constraints associated
with them, and that global symmetry only removes degrees of
freedom, albeit in phase space. For global symmetries such as Lorentz invariance, there is no first-class constraints associated
with them, and that global symmetry only removes 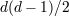 degrees of freedom. Technically, the counting should be
performed in phase space, but the results remains the same. See Section 7.1 for a more detailed review on the counting of
degrees of freedom. degrees of freedom. Technically, the counting should be
performed in phase space, but the results remains the same. See Section 7.1 for a more detailed review on the counting of
degrees of freedom. |
|
| 11 | Discretizing at the level of the metric leads to a mass term similar to (2.83*) which as we have seen contains a BD ghost. | |
| 12 | This special fully non-linear and Lorentz invariant theory of massive gravity, which has been proven in all generality to be free of the BD ghost in [295*, 296*] has since then be dubbed ‘dRGT’ theory. To avoid any confusion, we thus also call this ghost-free theory of massive gravity, the dRGT theory. | |
| 13 | The analysis performed in Ref. [95*] was unfortunately erroneous, and the conclusions of that paper are thus incorrect. | |
| 14 | In the previous section we obtained directly a theory of massive gravity, this should be seen as a trick to obtain a consistent theory of massive gravity. However, we shall see that we can take a decoupling limit of bi- (or even multi-)gravity so as to recover massive gravity and a decoupled massless spin-2 field. In this sense massive gravity is a perfectly consistent limit of bi-gravity. | |
| 15 | The field redefinition is local so no new degrees of freedom or other surprises hide in that field redefinition. | |
| 16 | See Refs. [169, 434, 242, 340] for additional work on deconstruction in five-dimensional AdS, and how this tackles the strong coupling issue. | |
| 17 | Some dofs may ‘accidentally’ disappear about some special backgrounds, but dofs cannot disappear non-linearly if they were present at the linearized level. | |
| 18 | More recently, Alexandrov impressively performed the full analysis for bi-gravity and massive gravity in the vielbein language [15*] determining the full set of primary and secondary constraints, confirming again the absence of BD ghost. This resolves the potential sources of subtleties raised in Refs. [96, 351, 349, 348]. | |
| 19 | We stress that multiplying with the matrix 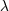 is not a projection, the equation (7.52*) contains as much information as
the equation of motion with respect to is not a projection, the equation (7.52*) contains as much information as
the equation of motion with respect to 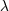 , multiplying the with the matrix , multiplying the with the matrix 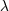 on both sides simply make the rank of the
equation more explicit. on both sides simply make the rank of the
equation more explicit. |
|
| 20 | If only 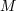 vielbein of the vielbein of the  vielbein are interacting there will be vielbein are interacting there will be 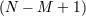 copies of diffeomorphism invariance
and copies of diffeomorphism invariance
and 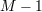 additional Hamiltonian constraints, leading to the correct number of dofs for additional Hamiltonian constraints, leading to the correct number of dofs for 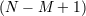 massless spin-2
fields and massless spin-2
fields and  massive spin-2 fields. massive spin-2 fields. |
|
| 21 | Technically, only one of them generates a first class constraint, while the  others generate a second-class
constraint. There are, therefore, others generate a second-class
constraint. There are, therefore, 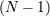 additional secondary constraints to be found by commuting the
primary constraint with the Hamiltonian, but the presence of these constraints at the linear level ensures that
they must exist at the non-linear level. There is also another subtlety in obtaining the secondary constraints
associated with the fact that the Hamiltonian is pure constraint, see the discussion in Section 7.1.3 for more
details. additional secondary constraints to be found by commuting the
primary constraint with the Hamiltonian, but the presence of these constraints at the linear level ensures that
they must exist at the non-linear level. There is also another subtlety in obtaining the secondary constraints
associated with the fact that the Hamiltonian is pure constraint, see the discussion in Section 7.1.3 for more
details. |
|
| 22 | This is actually precisely the way ghost-free massive gravity was originally constructed in [137*, 144*]. | |
| 23 | The non-renormalization theorem protects the parameters 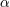 ’s and the mass from acquiring large quantum
corrections [140*, 146*] and it would be interesting to understand their implications in the case of a mass-varying
gravity. ’s and the mass from acquiring large quantum
corrections [140*, 146*] and it would be interesting to understand their implications in the case of a mass-varying
gravity. |
|
| 24 | Note that the Vainshtein mechanism does not occur for all parameters of the theory. In that case the massless limit does not reproduce GR. | |
| 25 | This result has been checked explicitly in Ref. [146*] using dimensional regularization or following the log divergences.
Taking power law divergences seriously would also allow for a scalings of the form 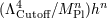 , which are no longer
suppressed by the mass scale , which are no longer
suppressed by the mass scale 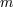 (although the mass scale (although the mass scale 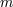 would never enter with negative powers at one loop.)
However, it is well known that power law divergences cannot be trusted as they depend on the measure of the
path integral and can lead to erroneous results in cases where the higher energy theory is known. See Ref. [84]
and references therein for known examples and an instructive discussion on the use and abuses of power law
divergences. would never enter with negative powers at one loop.)
However, it is well known that power law divergences cannot be trusted as they depend on the measure of the
path integral and can lead to erroneous results in cases where the higher energy theory is known. See Ref. [84]
and references therein for known examples and an instructive discussion on the use and abuses of power law
divergences. |
|
| 26 | If  , we can easily generalize the background solution to find other configurations that admit a superluminal
propagation. , we can easily generalize the background solution to find other configurations that admit a superluminal
propagation. |
|
| 27 | We thank the authors of [177*, 178*] for pointing this out. | |
| 28 | This is not to say that perturbations and/or perturbativity do not break down earlier in the quartic Galileon, see for instance Section 11.4 below as well as [88, 58], which is another sign that the Vainshtein mechanism works better in that case. | |
| 29 | The minimal model does not have a Vainshtein mechanism [435] in the static and spherically symmetric configuration so
in the limit 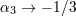 , or equivalently , or equivalently 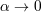 , we indeed expect an order one correction. , we indeed expect an order one correction. |
|
| 30 | In taking this limit, it is crucial that the second metric 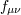 be written in a locally inertial coordinate system, i.e., a
system which is locally Minkowski. Failure to do this will lead to the erroneous conclusion that massive gravity on Minkowski
is not a limit of bi-gravity. be written in a locally inertial coordinate system, i.e., a
system which is locally Minkowski. Failure to do this will lead to the erroneous conclusion that massive gravity on Minkowski
is not a limit of bi-gravity. |
|
| 31 | In the context of DGP, the Friedmann equation was derived in Section 4.3.1 from the full five-dimensional picture, but one would have obtained the correct result if derived instead from the decoupling limit. The reason is the main modification of the Friedmann equation arises from the presence of the helicity-0 mode which is already captured in the decoupling limit. | |
| 32 | See [478*] for a recent review and more details. The convention on the parameters  there is related to our there is related to our 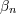 ’s here
via ’s here
via 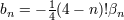 . . |
|
| 33 | Notice that this is not an issue in massive gravity with a flat reference metric since the analogue Friedmann equation does not even exist. | |
| 34 | Notice that even if massive gravity is formulated without the need of a reference metric, this does not change the fact that one copy of diffeomorphism invariance in broken leading to additional degrees of freedom as is the case in new massive gravity. | |
| 35 | See also [335, 195, 49, 50, 51] for other ghost-free non-local modifications of gravity, but where the graviton is massless. |

 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity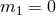
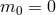 )
)