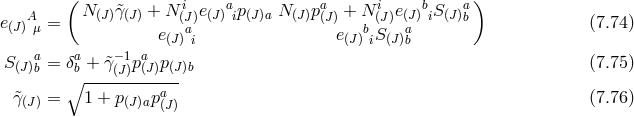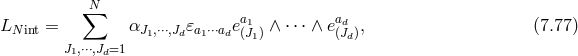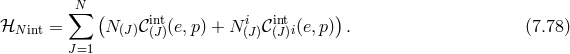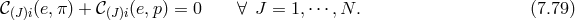7 Evading the BD Ghost in Massive Gravity
The deconstruction framework gave an intuitive approach on how to construct a theory of massive gravity or multiple interacting ‘gravitons’. This lead to the ghost-free dRGT theory of massive gravity and its bi- and multi-gravity extensions in a natural way. However, these developments were only possible a posteriori.The deconstruction framework was proposed earlier (see Refs. [24, 25, 168*, 28, 443, 168, 170]) directly in the metric language and despite starting from a perfectly healthy five-dimensional theory of GR, the discretization in the metric language leads to the standard BD issue (this also holds in a KK decomposition when truncating the KK tower at some finite energy scale). Knowing that massive gravity (or multi-gravity) can be naturally derived from a healthy five-dimensional theory of GR is thus not a sufficient argument for the absence of the BD ghost, and a great amount of effort was devoted to that proof, which is known by now a multitude of different forms and languages.
Within this review, one cannot make justice to all the independent proofs that have been formulated by now in the literature. We thus focus on a few of them – the Hamiltonian analysis in the ADM language – as well as the analysis in the Stückelberg language. One of the proofs in the vielbein formalism will be used in the multi-gravity case, and thus we do not emphasize that proof in the context of massive gravity, although it is perfectly applicable (and actually very elegant) in that case. Finally, after deriving the decoupling limit in Section 8.3, we also briefly review how it can be used to prove the absence of ghost more generically.
We note that even though the original argument on how the BD ghost could be circumvented in the full nonlinear theory was presented in [137*] and [144*], the absence of BD ghost in “ghost-free massive gravity” or dRGT has been the subject of many discussions [12, 13, 345*, 342*, 95, 341, 344, 96*] (see also [350, 351*, 349*, 348*, 352] for related discussions in bi-gravity). By now the confusion has been clarified, and see for instance [295*, 294*, 400*, 346, 343*, 297*, 15*, 259*] for thorough proofs addressing all the issues raised in the previous literature. (See also [347] for the proof of the absence of ghosts in other closely related models).
7.1 ADM formulation
7.1.1 ADM formalism for GR
Before going onto the subtleties associated with massive gravity, let us briefly summarize how the counting of the number of degrees of freedom can be performed in the ADM language using the Hamiltonian for GR. Using an ADM decomposition (where this time, we single out the time, rather than the extra dimension as was performed in Part I),
with the lapse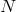 , the shift
, the shift 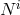 and the 3-dimensional space metric
and the 3-dimensional space metric 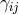 . In this section indices are
raised and lowered with respect to
. In this section indices are
raised and lowered with respect to 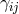 and dots represent derivatives with respect to
and dots represent derivatives with respect to 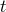 . In terms of these
variables, the action density for GR is
where
. In terms of these
variables, the action density for GR is
where 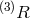 is the three-dimensional scalar curvature built out of
is the three-dimensional scalar curvature built out of  (no time derivatives in
(no time derivatives in 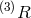 ) and
) and
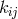 is the three-dimensional extrinsic curvature,
The GR action can thus be expressed in a way which has no double or higher time derivatives and only first
time-derivatives squared of
is the three-dimensional extrinsic curvature,
The GR action can thus be expressed in a way which has no double or higher time derivatives and only first
time-derivatives squared of 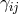 . This means that neither the shift nor the lapse are truly dynamical and
they do not have any associated conjugate momenta. The conjugate momentum associated with
. This means that neither the shift nor the lapse are truly dynamical and
they do not have any associated conjugate momenta. The conjugate momentum associated with 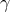 is,
We can now construct the Hamiltonian density for GR in terms of the 12 phase space variables (
is,
We can now construct the Hamiltonian density for GR in terms of the 12 phase space variables (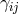 and
and
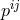 carry 6 component each),
So we see that in GR, both the shift and the lapse play the role of Lagrange multipliers. Thus they
propagate a first-class constraint each which removes 2 phase space degrees of freedom per
constraint. The counting of the number of degrees of freedom in phase space thus goes as follows:
corresponding to a total of 4 degrees of freedom in phase space, or 2 independent degrees of freedom in field
space. This is the very well-known and established result that in four dimensions GR propagates 2 physical
degrees of freedom, or gravitational waves have two polarizations.
carry 6 component each),
So we see that in GR, both the shift and the lapse play the role of Lagrange multipliers. Thus they
propagate a first-class constraint each which removes 2 phase space degrees of freedom per
constraint. The counting of the number of degrees of freedom in phase space thus goes as follows:
corresponding to a total of 4 degrees of freedom in phase space, or 2 independent degrees of freedom in field
space. This is the very well-known and established result that in four dimensions GR propagates 2 physical
degrees of freedom, or gravitational waves have two polarizations.
This result is fully generalizable to any number of dimensions, and in 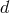 spacetime dimensions,
gravitational waves carry
spacetime dimensions,
gravitational waves carry 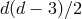 polarizations. We now move to the case of massive gravity.
polarizations. We now move to the case of massive gravity.
7.1.2 ADM counting in massive gravity
We now amend the GR Lagrangian with a potential 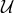 . As already explained, this can only be performed
by breaking covariance (with the exception of a cosmological constant). This potential could be a priori an
arbitrary function of the metric, but contains no derivatives and so does not affect the definition of the
conjugate momenta
. As already explained, this can only be performed
by breaking covariance (with the exception of a cosmological constant). This potential could be a priori an
arbitrary function of the metric, but contains no derivatives and so does not affect the definition of the
conjugate momenta 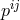 This translates directly into a potential at the level of the Hamiltonian density,
This translates directly into a potential at the level of the Hamiltonian density,
If 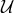 depends non-linearly on the shift or the lapse then these are no longer directly Lagrange
multipliers (if they are non-linear, they still appear at the level of the equations of motion, and so they do
not propagate a constraint for the metric but rather for themselves). As a result for an arbitrary potential
one is left with
depends non-linearly on the shift or the lapse then these are no longer directly Lagrange
multipliers (if they are non-linear, they still appear at the level of the equations of motion, and so they do
not propagate a constraint for the metric but rather for themselves). As a result for an arbitrary potential
one is left with 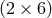 degrees of freedom in the three-dimensional metric and its momentum conjugate
and no constraint is present to reduce the phase space. This leads to
degrees of freedom in the three-dimensional metric and its momentum conjugate
and no constraint is present to reduce the phase space. This leads to 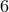 degrees of freedom in field space:
the two usual transverse polarizations for the graviton (as we have in GR), in addition to two ‘vector’
polarizations and two ‘scalar’ polarizations.
degrees of freedom in field space:
the two usual transverse polarizations for the graviton (as we have in GR), in addition to two ‘vector’
polarizations and two ‘scalar’ polarizations.
These 6 polarizations correspond to the five healthy massive spin-2 field degrees of freedom in addition to the sixth BD ghost, as explained in Section 2.5 (see also Section 7.2).
This counting is also generalizable to an arbitrary number of dimensions, in 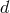 spacetime dimensions, a
massive spin-2 field should propagate the same number of degrees of freedom as a massless spin-2
field in
spacetime dimensions, a
massive spin-2 field should propagate the same number of degrees of freedom as a massless spin-2
field in 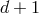 dimensions, that is
dimensions, that is 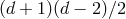 polarizations. However, an arbitrary
potential would allow for
polarizations. However, an arbitrary
potential would allow for 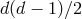 independent degrees of freedom, which is 1 too many
excitations, always corresponding to one BD ghost degree of freedom in an arbitrary number of
dimensions.
independent degrees of freedom, which is 1 too many
excitations, always corresponding to one BD ghost degree of freedom in an arbitrary number of
dimensions.
The only way this counting can be wrong is if the constraints for the shift and the lapse cannot be
inverted for the shift and the lapse themselves, and thus at least one of the equations of motion from the
shift or the lapse imposes a constraint on the three-dimensional metric  . This loophole was first
presented in [138] and an example was provided in [137*]. It was then used in [144*] to explain how the
‘no-go’ on the presence of a ghost in massive gravity could be circumvented. Finally, this argument was then
carried through fully non-linearly in [295*] (see also [342*] for the analysis in
. This loophole was first
presented in [138] and an example was provided in [137*]. It was then used in [144*] to explain how the
‘no-go’ on the presence of a ghost in massive gravity could be circumvented. Finally, this argument was then
carried through fully non-linearly in [295*] (see also [342*] for the analysis in  dimensions as presented
in [144*]).
dimensions as presented
in [144*]).
7.1.3 Eliminating the BD ghost
Linear Fierz–Pauli massive gravity
Fierz–Pauli massive gravity is special in that at the linear level (quadratic in the Hamiltonian), the lapse
remains linear, so it still acts as a Lagrange multiplier generating a primary second-class constraint.
Defining the metric as 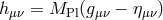 , (where for simplicity and definiteness we take Minkowski as
the reference metric
, (where for simplicity and definiteness we take Minkowski as
the reference metric 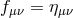 , although most of what follows can be easily generalizable to an arbitrary
reference metric
, although most of what follows can be easily generalizable to an arbitrary
reference metric 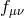 ). Expanding the lapse as
). Expanding the lapse as 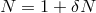 , we have
, we have 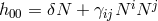 and
and
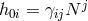 . In the ADM decomposition, the Fierz–Pauli mass term is then (see Eq. (2.45*))
. In the ADM decomposition, the Fierz–Pauli mass term is then (see Eq. (2.45*))
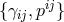 and remove at least half of the unwanted BD ghost. The
shift, on the other hand, is non-linear already in the Fierz–Pauli theory, so their equations of motion impose
a relation for themselves rather than a constraint for the three-dimensional metric. As a result the
Fierz–Pauli theory (at that order) propagates three additional degrees of freedom than GR, which are the
usual five degrees of freedom of a massive spin-2 field. Non-linearly however the Fierz–Pauli mass term
involve a non-linear term in the lapse in such a way that the constraint associated with it disappears and
Fierz–Pauli massive gravity has a ghost at the non-linear level, as pointed out in [75]. This is in
complete agreement with the discussion in Section 2.5, and is a complementary way to see the
issue.
and remove at least half of the unwanted BD ghost. The
shift, on the other hand, is non-linear already in the Fierz–Pauli theory, so their equations of motion impose
a relation for themselves rather than a constraint for the three-dimensional metric. As a result the
Fierz–Pauli theory (at that order) propagates three additional degrees of freedom than GR, which are the
usual five degrees of freedom of a massive spin-2 field. Non-linearly however the Fierz–Pauli mass term
involve a non-linear term in the lapse in such a way that the constraint associated with it disappears and
Fierz–Pauli massive gravity has a ghost at the non-linear level, as pointed out in [75]. This is in
complete agreement with the discussion in Section 2.5, and is a complementary way to see the
issue.
In Ref. [111*], the most general potential was considered up to quartic order in the 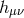 , and it was
shown that there is no choice of such potential (apart from a pure cosmological constant) which would
prevent the lapse from entering non-linearly. While this result is definitely correct, it does not however
imply the absence of a constraint generated by the set of shift and lapse
, and it was
shown that there is no choice of such potential (apart from a pure cosmological constant) which would
prevent the lapse from entering non-linearly. While this result is definitely correct, it does not however
imply the absence of a constraint generated by the set of shift and lapse 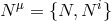 . Indeed
there is no reason to believe that the lapse should necessarily be the quantity to generates the
constraint necessary to remove the BD ghost. Rather it can be any combination of the lapse and the
shift.
. Indeed
there is no reason to believe that the lapse should necessarily be the quantity to generates the
constraint necessary to remove the BD ghost. Rather it can be any combination of the lapse and the
shift.
Example on how to evade the BD ghost non-linearly
As an instructive example presented in [137*], consider the following Hamiltonian,
with the following example for the potential In this example neither the lapse nor the shift enter linearly, and one might worry on the loss of the constraint to project out the BD ghost. However, upon solving for the shift and substituting back into the Hamiltonian (this is possible since the lapse is not dynamical), we get and the lapse now appears as a Lagrange multiplier generating a constraint, even though it was not linear in (7.10*). This could have been seen more easily, without the need to explicitly integrating out the shift by computing the Hessian In the example (7.10*), one has The Hessian cannot be inverted, which means that the equations of motion cannot be solved for all the shift and the lapse. Instead, one of these ought to be solved for the three-dimensional phase space variables which corresponds to the primary second-class constraint. Note that this constraint is not associated with a symmetry in this case and while the Hamiltonian is then pure constraint in this toy example, it will not be in general.Finally, one could also have deduce the existence of a constraint by performing the linear change of variable
in terms of which the Hamiltonian is then explicitly linear in the lapse, and generates a constraint that can be read for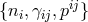 .
.
Condition to evade the ghost
To summarize, the condition to eliminate (at least half of) the BD ghost is that the 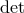 of the
Hessian (7.13*)
of the
Hessian (7.13*) 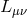 vanishes as explained in [144*]. This was shown to be the case in the
ghost-free theory of massive gravity (6.3*) [(6.1*)] exactly in some cases and up to quartic order,
and then fully non-linearly in [295*]. We summarize the derivation in the general case in what
follows.
vanishes as explained in [144*]. This was shown to be the case in the
ghost-free theory of massive gravity (6.3*) [(6.1*)] exactly in some cases and up to quartic order,
and then fully non-linearly in [295*]. We summarize the derivation in the general case in what
follows.
Ultimately, this means that in massive gravity we should be able to find a new shift 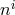 related to the
original one as follows
related to the
original one as follows 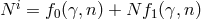 , such that the Hamiltonian takes the following
factorizable form
, such that the Hamiltonian takes the following
factorizable form
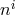 manifestly keeps the Hamiltonian linear in the lapse and has the
constraint
manifestly keeps the Hamiltonian linear in the lapse and has the
constraint 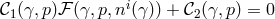 . However, such a field redefinition has not
(yet) been found. Instead, the new shift
. However, such a field redefinition has not
(yet) been found. Instead, the new shift 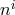 found below does the next best thing (which is
entirely sufficient) of a. Keeping the Hamiltonian linear in the lapse and b. Keeping its own
equation of motion independent of the lapse, which is sufficient to infer the presence of a primary
constraint.
found below does the next best thing (which is
entirely sufficient) of a. Keeping the Hamiltonian linear in the lapse and b. Keeping its own
equation of motion independent of the lapse, which is sufficient to infer the presence of a primary
constraint.
Primary constraint
We now proceed by deriving the primary first-class constraint present in ghost-free (dRGT) massive gravity.
The proof works equally well for any reference at no extra cost, and so we consider a general reference
metric 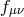 in its own ADM decomposition, while keep the dynamical metric
in its own ADM decomposition, while keep the dynamical metric 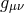 in its
original ADM form (since we work in unitary gauge, we may not simplify the metric further),
in its
original ADM form (since we work in unitary gauge, we may not simplify the metric further),
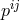 the conjugate momentum associated with
the conjugate momentum associated with 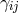 .
. 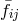 is not dynamical in massive
gravity so there is no conjugate momenta associated with it. The bars on the reference metric are there to
denote that these quantities are parameters of the theory and not dynamical variables, although the proof
for a dynamical reference metric and multi-gravity works equally well, this is performed in
Section 7.4.
is not dynamical in massive
gravity so there is no conjugate momenta associated with it. The bars on the reference metric are there to
denote that these quantities are parameters of the theory and not dynamical variables, although the proof
for a dynamical reference metric and multi-gravity works equally well, this is performed in
Section 7.4.
Proceeding similarly as in the previous example, we perform a change of variables similar as in (7.15*)
(only more complicated, but which remains linear in the lapse when expressing 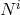 in terms of
in terms of
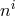 ) [295*, 296*]
) [295*, 296*]
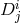 satisfies the following relation
with
In what follows we use the definition
with
satisfies the following relation
with
In what follows we use the definition
with
The field redefinition naturally involves a square root through the expression of the matrix 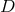 in (7.21*), which should come as no surprise from the square root structure of the potential term.
For the potential to be writable in the metric language, the square root in the definition of
the tensor
in (7.21*), which should come as no surprise from the square root structure of the potential term.
For the potential to be writable in the metric language, the square root in the definition of
the tensor 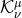 should exist, which in turns imply that the square root in the definition of
should exist, which in turns imply that the square root in the definition of
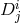 in (7.21*) must also exist. While complicated, the important point to notice is that this
field redefinition remains linear in the lapse (and so does not spoil the standard constraints of
GR).
in (7.21*) must also exist. While complicated, the important point to notice is that this
field redefinition remains linear in the lapse (and so does not spoil the standard constraints of
GR).
The Hamiltonian for massive gravity is then
where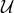 includes the new contributions from the mass term.
includes the new contributions from the mass term. 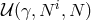 is neither linear in the lapse
is neither linear in the lapse
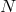 , nor in the shift
, nor in the shift 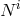 . There is actually no choice of potential
. There is actually no choice of potential 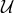 which would keep it linear in the
lapse beyond cubic order [111*]. However, as we shall see, when expressed in terms of the redefined
shift
which would keep it linear in the
lapse beyond cubic order [111*]. However, as we shall see, when expressed in terms of the redefined
shift 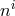 , the non-linearities in the shift absorb all the original non-linearities in the lapse
and
, the non-linearities in the shift absorb all the original non-linearities in the lapse
and 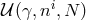 . In itself this is not sufficient to prove the presence of a constraint, as the
integration over the shift
. In itself this is not sufficient to prove the presence of a constraint, as the
integration over the shift 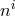 could in turn lead to higher order lapse in the Hamiltonian,
with
where the
could in turn lead to higher order lapse in the Hamiltonian,
with
where the 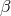 ’s are expressed in terms of the
’s are expressed in terms of the 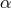 ’s as in (6.28*). For the purpose of this analysis it is easier
to work with that notation.
’s as in (6.28*). For the purpose of this analysis it is easier
to work with that notation.
The structure of the potential is so that the equations of motion with respect to the shift
are independent of the lapse 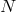 and impose the following relations in terms of
and impose the following relations in terms of 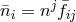 ,
,
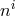 in terms of
in terms of 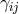 and
and 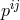 as well as the reference metric
as well as the reference metric 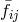 (note that
(note that 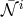 entirely disappears from these equations of motion).
entirely disappears from these equations of motion).
The two requirements defined previously are thus satisfied: a. The Hamiltonian is linear in the lapse and
b. the equations of motion with respect to the shift 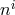 are independent of the lapse, which is
sufficient to infer the presence of a primary constraint. This primary constraint is derived by
varying with respect to the lapse and evaluating the shift on the constraint surface (7.29*),
are independent of the lapse, which is
sufficient to infer the presence of a primary constraint. This primary constraint is derived by
varying with respect to the lapse and evaluating the shift on the constraint surface (7.29*),
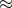 ” means on the constraint surface. The existence of this primary constraint is
sufficient to infer the absence of BD ghost. If we were dealing with a generic system (which could allow for
some spontaneous parity violation), it could still be in principle that there are no secondary
constraints associated with
” means on the constraint surface. The existence of this primary constraint is
sufficient to infer the absence of BD ghost. If we were dealing with a generic system (which could allow for
some spontaneous parity violation), it could still be in principle that there are no secondary
constraints associated with 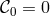 and the theory propagates 5.5 physical degrees of freedom (11
dofs in phase space). However, physically this never happens in the theory of gravity we are
dealing with preserves parity and is Lorentz invariant. Indeed, to have 5.5 physical degrees of
freedom, one of the variables should have an equation of motion which is linear in time derivatives.
Lorentz invariance then implies that it must also be linear in space derivatives which would then
violate parity. However, this is only an intuitive argument and the real proof is presented below.
Indeed, it ghost-free massive gravity admits a secondary constraint which was explicitly found
in [294*].
and the theory propagates 5.5 physical degrees of freedom (11
dofs in phase space). However, physically this never happens in the theory of gravity we are
dealing with preserves parity and is Lorentz invariant. Indeed, to have 5.5 physical degrees of
freedom, one of the variables should have an equation of motion which is linear in time derivatives.
Lorentz invariance then implies that it must also be linear in space derivatives which would then
violate parity. However, this is only an intuitive argument and the real proof is presented below.
Indeed, it ghost-free massive gravity admits a secondary constraint which was explicitly found
in [294*].
Secondary constraint
Let us imagine we start with initial conditions that satisfy the constraints of the system, in particular the modified Hamiltonian constraint (7.30*). As the system evolves the constraint (7.30*) needs to remain satisfied. This means that the modified Hamiltonian constraint ought to be independent of time, or in other words it should commute with the Hamiltonian. This requirement generates a secondary constraint,
with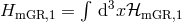 and
Finding the precise form of this secondary constraint requires a very careful analysis of the Poisson bracket
algebra of this system. This formidable task lead to some confusions at first (see Refs. [345]) but was then
successfully derived in [294*] (see also [258, 259] and [343]). Deriving the whole set of Poisson brackets is
beyond the scope of this review and we simply give the expression for the secondary constraint,
where unless specified otherwise, all indices are raised and lowered with respect to the dynamical metric
and
Finding the precise form of this secondary constraint requires a very careful analysis of the Poisson bracket
algebra of this system. This formidable task lead to some confusions at first (see Refs. [345]) but was then
successfully derived in [294*] (see also [258, 259] and [343]). Deriving the whole set of Poisson brackets is
beyond the scope of this review and we simply give the expression for the secondary constraint,
where unless specified otherwise, all indices are raised and lowered with respect to the dynamical metric
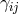 , and the covariant derivatives are also taken with respect to the same metric. We also define
, and the covariant derivatives are also taken with respect to the same metric. We also define
The important point to notice is that the secondary constraint (7.33*) only depends on the phase space
variables 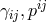 and not on the lapse
and not on the lapse 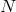 . Thus it constraints the phase space variables rather than the
lapse and provides a genuine secondary constraint in addition to the primary one (7.30*) (indeed one can
check that
. Thus it constraints the phase space variables rather than the
lapse and provides a genuine secondary constraint in addition to the primary one (7.30*) (indeed one can
check that 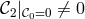 .).
.).
Finally, we should also check that this secondary constraint is also maintained in time. This was performed [294*], by inspecting the condition
This condition should be satisfied without further constraining the phase space variables, which would otherwise imply that fewer than five degrees of freedom are propagating. Since five fully fledged dofs are propagating at the linearized level, the same must happen non-linearly.17 Rather than a constraint on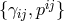 , (7.36*) must be solved for the lapse. This is only possible if both the
two following conditions are satisfied
As shown in [294*], since these conditions do not vanish at the linear level (the constraints reduce to the
Fierz–Pauli ones in that case), we can deduce that they cannot vanish non-linearly and thus the
condition (7.36*) fixes the expression for the lapse rather than constraining further the phase space dofs.
Thus there is no tertiary constraint on the phase space.
, (7.36*) must be solved for the lapse. This is only possible if both the
two following conditions are satisfied
As shown in [294*], since these conditions do not vanish at the linear level (the constraints reduce to the
Fierz–Pauli ones in that case), we can deduce that they cannot vanish non-linearly and thus the
condition (7.36*) fixes the expression for the lapse rather than constraining further the phase space dofs.
Thus there is no tertiary constraint on the phase space.
To conclude, we have shown in this section that ghost-free (or dRGT) massive gravity is indeed free from the BD ghost and the theory propagates five physical dofs about generic backgrounds. We now present the proof in other languages, but stress that the proof developed in this section is sufficient to infer the absence of BD ghost.
Secondary constraints in bi- and multi-gravity
In bi- or multi-gravity where all the metrics are dynamical the Hamiltonian is pure constraint (every term is linear in the one of the lapses as can be seen explicitly already from (7.25*) and (7.26*)).
In this case, the evolution equation of the primary constraint can always be solved for their respective Lagrange multiplier (lapses) which can always be set to zero. Setting the lapses to zero would be unphysical in a theory of gravity and instead one should take a ‘bifurcation’ of the Dirac constraint analysis as explained in [48*]. Rather than solving for the Lagrange multipliers we can choose to use the evolution equation of some of the primary constraints to provide additional secondary constraints instead of solving them for the lagrange multipliers.
Choosing this bifurcation leads to statements which are then continuous with the massive gravity case and one recovers the correct number of degrees of freedom. See Ref. [48] for an enlightening discussion.
7.2 Absence of ghost in the Stückelberg language
7.2.1 Physical degrees of freedom
Another way to see the absence of ghost in massive gravity is to work directly in the Stückelberg language
for massive spin-2 fields introduced in Section 2.4. If the four scalar fields 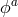 were dynamical, the
theory would propagate six degrees of freedom (the two usual helicity-2 which dynamics is
encoded in the standard Einstein–Hilbert term, and the four Stückelberg fields). To remove the
sixth mode, corresponding to the BD ghost, one needs to check that not all four Stückelberg
fields are dynamical but only three of them. See also [14] for a theory of two Stückelberg
fields.
were dynamical, the
theory would propagate six degrees of freedom (the two usual helicity-2 which dynamics is
encoded in the standard Einstein–Hilbert term, and the four Stückelberg fields). To remove the
sixth mode, corresponding to the BD ghost, one needs to check that not all four Stückelberg
fields are dynamical but only three of them. See also [14] for a theory of two Stückelberg
fields.
Stated more precisely, in the Stückelberg language beyond the DL, if 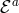 is the equation of motion
with respect to the field
is the equation of motion
with respect to the field 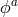 , the correct requirement for the absence of ghost is that the Hessian
, the correct requirement for the absence of ghost is that the Hessian 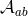 defined as
defined as
7.2.2 Two-dimensional case
Consider massive gravity on a two-dimensional space-time, 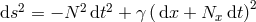 , with the
two Stückelberg fields
, with the
two Stückelberg fields 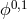 [145*]. In this case the graviton potential can only have one independent
non-trivial term, (excluding the tadpole),
[145*]. In this case the graviton potential can only have one independent
non-trivial term, (excluding the tadpole),
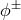 is then
and is clearly non-invertible, which shows that not both Stückelberg fields are dynamical.
In this special case, the Hamiltonian is actually pure constraint as shown in [145*], and there
are no propagating degrees of freedom. This is as expected for a massive spin-two field in two
dimensions.
is then
and is clearly non-invertible, which shows that not both Stückelberg fields are dynamical.
In this special case, the Hamiltonian is actually pure constraint as shown in [145*], and there
are no propagating degrees of freedom. This is as expected for a massive spin-two field in two
dimensions.
As shown in Refs. [144*, 145] the square root can be traded for an auxiliary non-dynamical variable
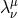 . In this two-dimensional example, the mass term (7.43*) can be rewritten with the help of an auxiliary
non-dynamical variable
. In this two-dimensional example, the mass term (7.43*) can be rewritten with the help of an auxiliary
non-dynamical variable 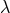 as
as
7.2.3 Full proof
The full proof in the minimal model (corresponding to 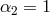 and
and 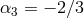 and
and 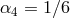 in (6.3*)
or
in (6.3*)
or 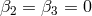 in the alternative formulation (6.23*)), was derived in Ref. [297*]. We briefly review the
essence of the argument, although the full technical derivation is beyond the scope of this review and refer
the reader to Refs. [297*] and [15] for a fully-fledged derivation.
in the alternative formulation (6.23*)), was derived in Ref. [297*]. We briefly review the
essence of the argument, although the full technical derivation is beyond the scope of this review and refer
the reader to Refs. [297*] and [15] for a fully-fledged derivation.
Using a set of auxiliary variables 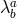 (with
(with 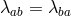 , so these auxiliary variables contain ten
elements in four dimensions) as explained previously, we can rewrite the potential term in the minimal
model as [79, 342],
, so these auxiliary variables contain ten
elements in four dimensions) as explained previously, we can rewrite the potential term in the minimal
model as [79, 342],
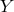 has been defined in (2.77*) and is equivalent to
has been defined in (2.77*) and is equivalent to 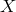 used previously. Upon
integration over the auxiliary variable
used previously. Upon
integration over the auxiliary variable 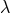 we recover the square-root structure as mentioned in Ref. [144*].
We now perform an ADM decomposition as in (7.1*) which implies the ADM decomposition on the matrix
we recover the square-root structure as mentioned in Ref. [144*].
We now perform an ADM decomposition as in (7.1*) which implies the ADM decomposition on the matrix
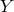 ,
with
Since the matrix
,
with
Since the matrix 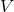 uses a projection along the 3 spatial directions it is genuinely a rank-3 matrix rather
than rank 4. This implies that
uses a projection along the 3 spatial directions it is genuinely a rank-3 matrix rather
than rank 4. This implies that 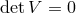 . Notice that we consider an arbitrary reference metric
. Notice that we consider an arbitrary reference metric 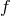 , as
the proof does not depend on it and can be done for any
, as
the proof does not depend on it and can be done for any 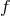 at no extra cost [297*]. The canonical momenta
conjugate to
at no extra cost [297*]. The canonical momenta
conjugate to 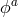 is given by
with
In terms of these conjugate momenta, the equations of motion with respect to
is given by
with
In terms of these conjugate momenta, the equations of motion with respect to 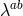 then imposes the relation (after multiplying
with the matrix19
then imposes the relation (after multiplying
with the matrix19
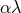 on both side),
with the matrix
on both side),
with the matrix 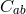 defined as
Since
defined as
Since 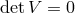 , as mentioned previously, the equation of motion (7.52*) is only consistent if we also have
, as mentioned previously, the equation of motion (7.52*) is only consistent if we also have
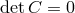 . This is the first constraint found in [297*] which is already sufficient to remove (half) the BD
ghost,
which is the primary constraint on a subset of physical phase space variables
. This is the first constraint found in [297*] which is already sufficient to remove (half) the BD
ghost,
which is the primary constraint on a subset of physical phase space variables 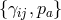 , (by construction
, (by construction
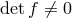 ). The secondary constraint is then derived by commuting
). The secondary constraint is then derived by commuting 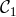 with the Hamiltonian. Following
the derivation of [297], we get on the constraint surface
where
with the Hamiltonian. Following
the derivation of [297], we get on the constraint surface
where 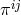 is the momentum conjugate associated with
is the momentum conjugate associated with 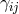 , and
, and 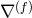 is the covariant derivative
associated with
is the covariant derivative
associated with 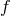 .
.
7.2.4 Stückelberg method on arbitrary backgrounds
When working about different non-Minkowski backgrounds, one can instead generalize the definition of the helicity-0 mode as was performed in [400*]. The essence of the argument is to perform a rotation in field space so that the fluctuations of the Stückelberg fields about a curved background form a vector field in the new basis, and one can then employ the standard treatment for a vector field. See also [10] for another study of the Stückelberg fields in an FLRW background.
Recently, a covariant Stückelberg analysis valid about any background was performed in Ref. [369*] using the BRST formalism. Interestingly, this method also allows to derive the decoupling limit of massive gravity about any background.
In what follows, we review the approach derived in [400*] which provides yet another independent argument for the absence of ghost in all generalities. The proofs presented in Sections 7.1 and 7.2 work to all orders about a trivial background while in [400*], the proof is performed about a generic (curved) background, and the analysis can thus stop at quadratic order in the fluctuations. Both types of analysis are equivalent so long as the fields are analytic, which is the case if one wishes to remain within the regime of validity of the theory.
Consider a generic background metric, which in unitary gauge (i.e., in the coordinate system
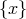 where the Stückelberg background fields are given by
where the Stückelberg background fields are given by 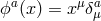 ), the background
metric is given by
), the background
metric is given by 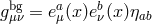 , and the background Stückelberg fields are given by
, and the background Stückelberg fields are given by
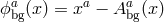 .
.
We now add fluctuations about that background,
with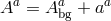 .
.
Flat background metric
First, note that if we consider a flat background metric to start with, then at zeroth order
in 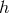 , the ghost-free potential is of the form [400*], (this can also be seen from [238*, 419*])
, the ghost-free potential is of the form [400*], (this can also be seen from [238*, 419*])
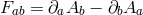 . This means that for a symmetric Stückelberg background configuration, i.e., if
the matrix
. This means that for a symmetric Stückelberg background configuration, i.e., if
the matrix 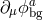 is symmetric, then
is symmetric, then 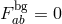 , and at quadratic order in the fluctuation
, and at quadratic order in the fluctuation  , the action
has a
, the action
has a 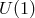 -symmetry. This symmetry is lost non-linearly, but is still relevant when looking at quadratic
fluctuations about arbitrary backgrounds. Now using the split about the background,
-symmetry. This symmetry is lost non-linearly, but is still relevant when looking at quadratic
fluctuations about arbitrary backgrounds. Now using the split about the background, 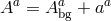 , this
means that up to quadratic order in the fluctuations
, this
means that up to quadratic order in the fluctuations 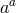 , the action at zeroth order in the metric
fluctuation is of the form [400]
with
, the action at zeroth order in the metric
fluctuation is of the form [400]
with 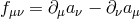 and
and 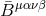 is a set of constant coefficients which depends on
is a set of constant coefficients which depends on 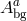 . This
quadratic action has an accidental
. This
quadratic action has an accidental 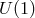 -symmetry which is responsible for projecting out one of the four
dofs naively present in the four Stückelberg fluctuations
-symmetry which is responsible for projecting out one of the four
dofs naively present in the four Stückelberg fluctuations 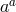 . Had we considered any other potential term,
the
. Had we considered any other potential term,
the 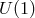 symmetry would have been generically lost and all four Stückelberg fields would have been
dynamical.
symmetry would have been generically lost and all four Stückelberg fields would have been
dynamical.
Non-symmetric background Stückelberg
If the background configuration is not symmetric, then at every point one needs to perform first an internal
Lorentz transformation 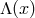 in the Stückelberg field space, so as to align them with the coordinate basis
and recover a symmetric configuration for the background Stückelberg fields. In this new Lorentz frame,
the Stückelberg fluctuation is
in the Stückelberg field space, so as to align them with the coordinate basis
and recover a symmetric configuration for the background Stückelberg fields. In this new Lorentz frame,
the Stückelberg fluctuation is 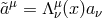 . As a result, to quadratic order in the Stückelberg
fluctuation the part of the ghost-free potential which is independent of the metric fluctuation and
its curvature goes symbolically as (7.60*) with
. As a result, to quadratic order in the Stückelberg
fluctuation the part of the ghost-free potential which is independent of the metric fluctuation and
its curvature goes symbolically as (7.60*) with 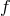 replaced by
replaced by 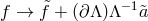 , (with
, (with
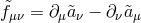 ). Interestingly, the Lorentz boost
). Interestingly, the Lorentz boost 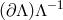 now plays the role of a mass term for
what looks like a gauge field
now plays the role of a mass term for
what looks like a gauge field 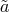 . This mass term breaks the
. This mass term breaks the 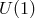 symmetry, but there is still no kinetic
term for
symmetry, but there is still no kinetic
term for 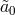 , very much as in a Proca theory. This part of the potential is thus manifestly ghost-free (in
the sense that it provides a dynamics for only three of the four Stückelberg fields, independently of the
background).
, very much as in a Proca theory. This part of the potential is thus manifestly ghost-free (in
the sense that it provides a dynamics for only three of the four Stückelberg fields, independently of the
background).
Next, we consider the mixing with metric fluctuation 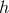 while still assuming zero curvature. At linear
order in
while still assuming zero curvature. At linear
order in 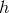 , the ghost-free potential, (6.3*) goes as follows
, the ghost-free potential, (6.3*) goes as follows
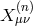 are similar to the ones found in the decoupling limit, but now expressed in terms
of the symmetric full four Stückelberg fields rather than just
are similar to the ones found in the decoupling limit, but now expressed in terms
of the symmetric full four Stückelberg fields rather than just  , i.e., replacing
, i.e., replacing  by
by 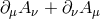 in the respective expressions (8.29*), (8.30*) and (8.31*) for
in the respective expressions (8.29*), (8.30*) and (8.31*) for 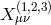 . Starting with the symmetric
configuration for the Stückelberg fields, then since we are working at the quadratic level in perturbations,
one of the
. Starting with the symmetric
configuration for the Stückelberg fields, then since we are working at the quadratic level in perturbations,
one of the 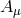 in the
in the 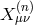 is taken to be the fluctuation
is taken to be the fluctuation 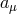 , while the others are taken to be the
background field
, while the others are taken to be the
background field 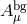 . As a result in the first terms in
. As a result in the first terms in 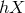 in (7.61*)
in (7.61*) 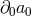 cannot come at the
same time as
cannot come at the
same time as 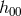 or
or 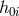 , and we can thus integrate by parts the time derivative acting
on any
, and we can thus integrate by parts the time derivative acting
on any 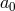 , leading to a harmless first time derivative on
, leading to a harmless first time derivative on 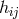 , and no time evolution for
, and no time evolution for
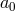 .
.
As for the second type of term in (7.61*), since 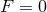 on the background field
on the background field 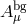 ,
the second type of terms is forced to be proportional to
,
the second type of terms is forced to be proportional to 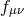 and cannot involve any
and cannot involve any 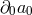 at all. As a result
at all. As a result 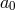 is not dynamical, which ensures that the theory is free from the BD
ghost.
is not dynamical, which ensures that the theory is free from the BD
ghost.
This part of the argument generalizes easily for non symmetric background Stückelberg configurations,
and the same replacement 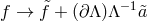 still ensures that
still ensures that 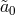 acquires no dynamics
from (7.61*).
acquires no dynamics
from (7.61*).
Background curvature
Finally, to complete the argument, we consider the effect from background curvature, then 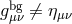 ,
with
,
with 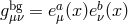 . The space-time curvature is another source of ‘misalignment’ between the
coordinates and the Stückelberg fields. To rectify for this misalignment, we could go two ways: Either
perform a local change of coordinate so as to align the background metric
. The space-time curvature is another source of ‘misalignment’ between the
coordinates and the Stückelberg fields. To rectify for this misalignment, we could go two ways: Either
perform a local change of coordinate so as to align the background metric 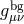 with the flat reference
metric
with the flat reference
metric 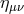 (i.e., going to local inertial frame), or the other way around: i.e., express the flat reference
metric in terms of the curved background metric,
(i.e., going to local inertial frame), or the other way around: i.e., express the flat reference
metric in terms of the curved background metric, 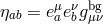 , in terms of the inverse vielbein,
, in terms of the inverse vielbein,
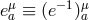 . Then the building block of ghost-free massive gravity is the matrix
. Then the building block of ghost-free massive gravity is the matrix 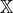 , defined previously
as
, defined previously
as
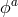 should be replaced by their ‘vielbein-dependent’ counterparts, i.e.,
should be replaced by their ‘vielbein-dependent’ counterparts, i.e.,
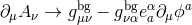 . In terms of the Stückelberg field fluctuation
. In terms of the Stückelberg field fluctuation 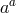 , this implies the
replacement
, this implies the
replacement 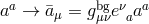 , and symbolically,
, and symbolically, 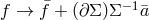 , with
, with 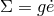 . The
situation is thus the same as when we were dealing with a non-symmetric Stückelberg background
configuration, after integration by parts (which might involve curvature harmless contributions), the
potential can be written in a way which never involves any time derivative on
. The
situation is thus the same as when we were dealing with a non-symmetric Stückelberg background
configuration, after integration by parts (which might involve curvature harmless contributions), the
potential can be written in a way which never involves any time derivative on  . As a result,
. As a result,
 plays the role of an effective Proca vector field which only propagates three degrees of
freedom, and this about any curved background metric. The beauty of this argument lies in the
correct identification of the proper degrees of freedom when dealing with a curved background
metric.
plays the role of an effective Proca vector field which only propagates three degrees of
freedom, and this about any curved background metric. The beauty of this argument lies in the
correct identification of the proper degrees of freedom when dealing with a curved background
metric.
7.3 Absence of ghost in the vielbein formulation
Finally, we can also prove the absence of ghost for dRGT in the Vielbein formalism, either directly at the level of the Lagrangian in some special cases as shown in [171*] or in full generality in the Hamiltonian formalism, as shown in [314*]. The later proof also works in all generality for a multi-gravity theory and will thus be presented in more depth in what follows, but we first focus on a special case presented in Ref. [171*].
Let us start with massive gravity in the vielbein formalism (6.1*). As was the case in Part II, we work
with the symmetric vielbein condition, 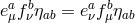 . For simplicity we specialize further to the case
where
. For simplicity we specialize further to the case
where 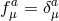 , so that the symmetric vielbein condition imposes
, so that the symmetric vielbein condition imposes 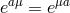 . Under this
condition, the vielbein contains as many independent components as the metric. The symmetric
veilbein condition ensures that one is able to reformulate the theory in a metric language. In
. Under this
condition, the vielbein contains as many independent components as the metric. The symmetric
veilbein condition ensures that one is able to reformulate the theory in a metric language. In 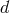 spacetime dimensions, there is a priori
spacetime dimensions, there is a priori 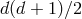 independent components in the symmetric
vielbein.
independent components in the symmetric
vielbein.
Varying the action (6.1*) with respect to the vielbein leads to the modified Einstein equation,
with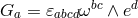 . From the Bianchi identity,
. From the Bianchi identity, 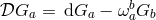 , we infer the
, we infer the 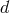 constraints
leading to
constraints
leading to 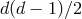 independent components in the vielbein. This is still one too many component,
unless an additional constraint is found. The idea behind the proof in Ref. [171*], is then to use the Bianchi
identities to infer an additional constraint of the form,
where
independent components in the vielbein. This is still one too many component,
unless an additional constraint is found. The idea behind the proof in Ref. [171*], is then to use the Bianchi
identities to infer an additional constraint of the form,
where 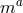 is an appropriate one-form which depends on the specific coefficients of the theory. Such a
constrain is present at the linear level for Fierz–Pauli massive gravity, and it was further shown in
Ref. [171*] that special choices of coefficients for the theory lead to remarkably simple analogous relations
fully non-linearly. To give an example, we consider all the coefficients
is an appropriate one-form which depends on the specific coefficients of the theory. Such a
constrain is present at the linear level for Fierz–Pauli massive gravity, and it was further shown in
Ref. [171*] that special choices of coefficients for the theory lead to remarkably simple analogous relations
fully non-linearly. To give an example, we consider all the coefficients 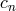 to vanish but
to vanish but 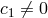 . In that
case the Bianchi identity (7.65*) implies
where similarly as in (5.2*), the torsionless connection is given in term of the vielbein as
with
. In that
case the Bianchi identity (7.65*) implies
where similarly as in (5.2*), the torsionless connection is given in term of the vielbein as
with ![oabc = 2eaμebν∂ [μeν]c](article1214x.gif) . The Bianchi identity (7.67*) then implies
. The Bianchi identity (7.67*) then implies ![eab∂[beaa] = 0](article1215x.gif) , so that we obtain an
extra constraint of the form (7.66*) with
, so that we obtain an
extra constraint of the form (7.66*) with 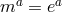 . Ref. [171] derived similar constraints for other
parameters of the theory.
. Ref. [171] derived similar constraints for other
parameters of the theory.
7.4 Absence of ghosts in multi-gravity
We now turn to the proof for the absence of ghost in multi-gravity and follow the vielbein
formulation of Ref. [314*]. In this subsection we use the notation that uppercase Latin indices
represent 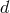 -dimensional Lorentz indices,
-dimensional Lorentz indices, 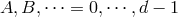 , while lowercase Latin
indices represent the
, while lowercase Latin
indices represent the  -dimensional Lorentz indices along the space directions after ADM
decomposition,
-dimensional Lorentz indices along the space directions after ADM
decomposition, 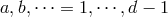 . Greek indices represent
. Greek indices represent 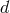 -dimensional spacetime indices
-dimensional spacetime indices
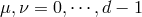 , while the ‘middle’ of the Latin alphabet indices
, while the ‘middle’ of the Latin alphabet indices 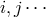 represent pure
space indices
represent pure
space indices 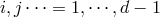 . Finally, capital indices label the metric and span over
. Finally, capital indices label the metric and span over
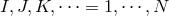 .
.
Let us start with 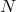 non-interacting spin-2 fields. The theory has then
non-interacting spin-2 fields. The theory has then 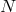 copies of coordinate
transformation invariance (the coordinate system associated with each metric can be changed separately),
as well as
copies of coordinate
transformation invariance (the coordinate system associated with each metric can be changed separately),
as well as 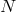 copies of Lorentz invariance. At this level may, for each vielbein
copies of Lorentz invariance. At this level may, for each vielbein 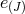 ,
, 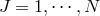 we
may use part of the Lorentz freedom to work in the upper triangular form for the vielbein,
we
may use part of the Lorentz freedom to work in the upper triangular form for the vielbein,
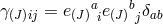 . Starting with non-interacting fields, we simply
take
. Starting with non-interacting fields, we simply
take 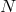 copies of the GR action,
and the Hamiltonian in terms of the vielbein variables then takes the form (7.6*)
where
copies of the GR action,
and the Hamiltonian in terms of the vielbein variables then takes the form (7.6*)
where 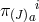 is the conjugate momentum associated with the vielbein
is the conjugate momentum associated with the vielbein 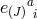 and the constraints
and the constraints
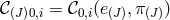 are the ones mentioned previously in (7.6*) (now expressed in the vielbein
variables) and are related to diffeomorphism invariance. In the vielbein language there is an addition
are the ones mentioned previously in (7.6*) (now expressed in the vielbein
variables) and are related to diffeomorphism invariance. In the vielbein language there is an addition
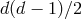 primary constraints for each vielbein field
related to the residual local Lorentz symmetry still present after fixing the upper triangular form for the
vielbeins.
primary constraints for each vielbein field
related to the residual local Lorentz symmetry still present after fixing the upper triangular form for the
vielbeins.
Now rather than setting part of the  Lorentz frames to be on the upper diagonal form for all the
Lorentz frames to be on the upper diagonal form for all the
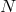 vielbein (7.69*) we only use one Lorentz boost to set one of the vielbein in that form, say
vielbein (7.69*) we only use one Lorentz boost to set one of the vielbein in that form, say
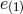 , and ‘unboost’ the
, and ‘unboost’ the  other frames, so that for any of the other vielbein one has
other frames, so that for any of the other vielbein one has
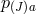 is the boost that would bring that vielbein in the upper diagonal form.
is the boost that would bring that vielbein in the upper diagonal form.
We now consider arbitrary interactions between the 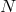 fields of the form (6.1*),
fields of the form (6.1*),
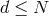 , otherwise the formalism is exactly the same (there is some
redundancy in this formulation, i.e., some interactions are repeated in this formulation, but this has no
consequence for the argument). Since the vielbeins
, otherwise the formalism is exactly the same (there is some
redundancy in this formulation, i.e., some interactions are repeated in this formulation, but this has no
consequence for the argument). Since the vielbeins 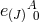 are linear in their respective shifts and lapse
are linear in their respective shifts and lapse
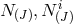 and the vielbeins
and the vielbeins 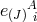 do not depend any shift nor lapse, it is easy to see that the general
set of interactions (7.77*) lead to a Hamiltonian which is also linear in every shift and lapse,
Indeed the wedge structure of (6.1*) or (7.77*) ensures that there is one and only one vielbein with time-like
index
do not depend any shift nor lapse, it is easy to see that the general
set of interactions (7.77*) lead to a Hamiltonian which is also linear in every shift and lapse,
Indeed the wedge structure of (6.1*) or (7.77*) ensures that there is one and only one vielbein with time-like
index 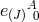 for every term
for every term 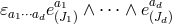 .
.
Notice that for the interactions, the terms 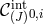 can depend on all the
can depend on all the 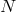 vielbeins
vielbeins 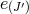 and all
the
and all
the  ‘boosts’
‘boosts’ 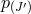 , (as mentioned previously, part of one Lorentz frame is set so that
, (as mentioned previously, part of one Lorentz frame is set so that 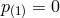 and
and 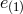 is in the upper diagonal form). Following the procedure of [314], we can now solve
for the
is in the upper diagonal form). Following the procedure of [314], we can now solve
for the  remaining boosts by using
remaining boosts by using 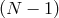 of the
of the 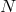 shift equations of motion
shift equations of motion
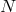 vielbein are
interacting,20
(i.e., there is no vielbein
vielbein are
interacting,20
(i.e., there is no vielbein 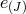 which does not appear at least once in the interactions (7.77*) which mix
different vielbeins), the shift equations (7.79*) will involve all the
which does not appear at least once in the interactions (7.77*) which mix
different vielbeins), the shift equations (7.79*) will involve all the  boosts and can be solved for them
without spoiling the linearity in any of the
boosts and can be solved for them
without spoiling the linearity in any of the 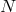 lapses
lapses 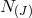 . As a result, the
. As a result, the  lapses
lapses 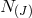 for
for
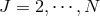 are Lagrange multiplier for
are Lagrange multiplier for 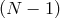 first class constraints. The lapse
first class constraints. The lapse 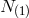 for the first
vielbein combines with the remaining shift
for the first
vielbein combines with the remaining shift 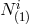 to generate the one remaining copy of diffeomorphism
invariance.
to generate the one remaining copy of diffeomorphism
invariance.
We now have all the ingredients to count the number of dofs in phase space: We start with
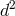 components in each of the
components in each of the 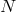 vielbein
vielbein 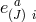 and associated conjugate momenta,
that is a total of
and associated conjugate momenta,
that is a total of 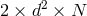 phase space variables. We then have
phase space variables. We then have 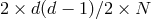 constraints21
associated with the
constraints21
associated with the 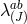 . There is one copy of diffeomorphism removing
. There is one copy of diffeomorphism removing 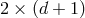 phase space dofs
(with Lagrange multiplier
phase space dofs
(with Lagrange multiplier 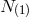 and
and 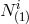 ) and
) and 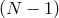 additional first-class constraints
with Lagrange multipliers
additional first-class constraints
with Lagrange multipliers 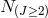 removing
removing 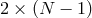 dofs. As a result we end up with
dofs. As a result we end up with
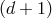 spacetime dimensions, and the theory is thus free of any BD
ghost.
spacetime dimensions, and the theory is thus free of any BD
ghost.

 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
 )
)
![∫ M-2Pl (√ --- [√ --- ]) ℒGR = 2 dt − gR + ∂t − g[k] (7.2 ) 2 ∫ = M-Pl dtN √ γ-((3)R [γ ] + [k]2 − [k2]), (7.3 ) 2](article962x.gif)



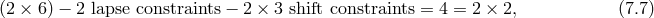
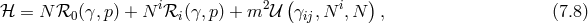
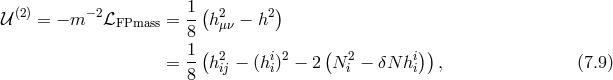
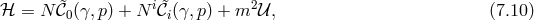

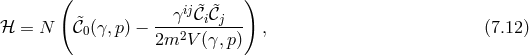
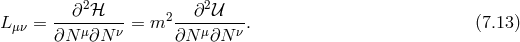
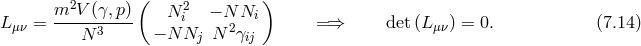

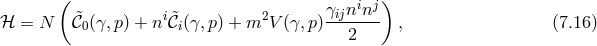
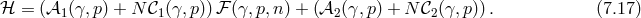
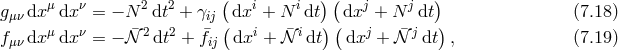
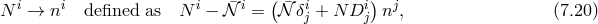




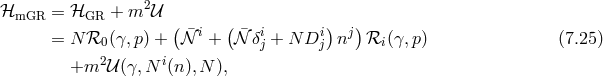
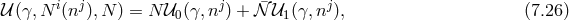
![M 2Pl√--∑3 (4 − n)βn i 𝒰0 = − -4-- γ ----n!----ℒn[ &tidle;D j] (7.27 ) n=0 M 2Pl√--( i j 𝒰1 = − ---- γ 3!β1κ + 2β2D jP i (7.28 ) 4[ ] ) 2 ∘ -- + β3κ 2D [kni] ¯fijDj nℓ + D [iDj ] − M-Plβ4 ¯f, k ℓ i j 4](article1042x.gif)
![[ ( ) ] m2 √ γ- 3!β1 ¯ni + 4β2 &tidle;Dj ¯ni] + β3D&tidle;[jj D&tidle;k ]k¯ni − 2 &tidle;Dki]¯nk = κℛi (γ,p), (7.29 ) [j](article1047x.gif)
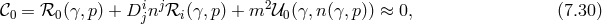
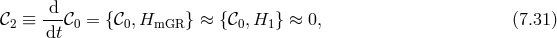
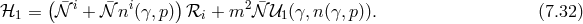

![ij 1 ∂𝒰1 𝒰 1 = √------- (7.34 ) γ ∂γij ( ) M-P2l[ −1 k β3- ℬ¯ij = − 4 (D&tidle; ) j ¯fik 3 β1ℒ0[ &tidle;D ] + 2β2ℒ1 [ &tidle;D] + 2 ℒ2 [ &tidle;D] (7.35 ) ] − β2f¯ij + 2 β3 ¯fi[k &tidle;Dkj] .](article1062x.gif)

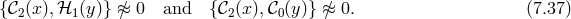



![ϕ± = ϕ0 ± ϕ1 (7.41 ) 1 1 [ ] 𝒟± = √--∂x ± ---∂t − Nx∂x , (7.42 ) γ N](article1078x.gif)
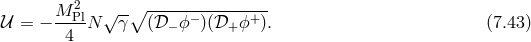
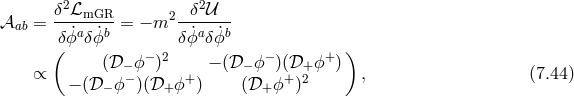
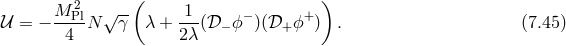
![M 2√ --- ( ) 𝒰 = ---Pl − g [λ ] + [λ−1 ⋅ Y ] , (7.46 ) 4](article1091x.gif)
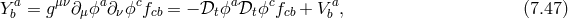





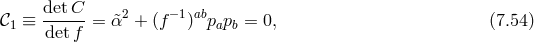
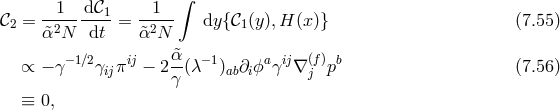



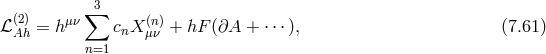
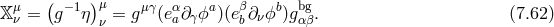
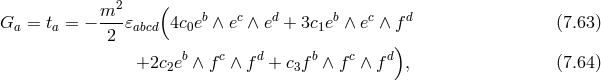




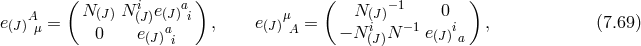
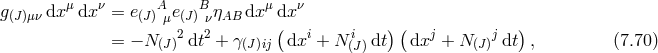
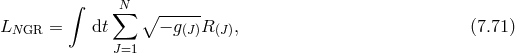
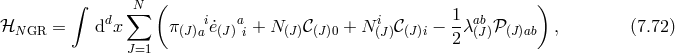
![i 𝒫(J)ab = e(J)[ai π (J)b], (7.73 )](article1241x.gif)